1. Đề thi vào 10 môn Toán Vĩnh Long năm 2021

Đề bài

Bài 1 (1,0 điểm): Tính giá trị các biểu thức:

a) \(A = 3\sqrt {18}  + 2\sqrt 8  – \sqrt {72} \)                                              b) \(B = \dfrac{{\sqrt 3  – \sqrt 6 }}{{1 – \sqrt 2 }} + \sqrt {{{\left( {2 – \sqrt 3 } \right)}^2}} \)

Bài 2 (2,0 điểm): Giải các phương trình và hệ phương trình sau:

a) \({x^2} – 8x + 15 = 0\)                                                        b) \(2{x^2} + 5x = 0\)

c) \(\left\{ \begin{array}{l}2x + y = 5\\5x – 2y = 8\end{array} \right.\)                                                      d) \(9{x^4} + 8{x^2} – 1 = 0\).

Bài 3 (2,0 điểm):

a) Trong mặt phẳng tọa độ \(Oxy\), cho hàm số \(y = \dfrac{1}{4}{x^2}\) có đồ thị \(\left( P \right)\) và đường thẳng \(\left( d \right):\,\,y =  – \dfrac{1}{2}x + 2\). Vẽ đồ thị \(\left( P \right)\) và \(\left( d \right)\) trên cùng một mặt phẳng tọa độ.

b) Cho phương trình \({x^2} – 2x + m – 1 = 0\) (\(x\) là ẩn số, \(m\) là tham số). Tìm \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 – {x_1}{x_2} + x_1^2x_2^2 – 14 = 0\).

Bài 4 (1,0 điểm): Hai vòi nước cùng chảy vào một bể không có nước thì sau 3 giờ đầy bể. Nếu mở vòi một chảy một mình trong 20 phút, rồi khóa lại, mở tiếp vòi hai chảy trong 30 phút thì cả hai vòi chảy được \(\dfrac{1}{8}\) bể. Tính thời gian mỗi vòi chảy một mình đầy bể.

Bài 5 (1,0 điểm): Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(AB = 9\,\,cm,\,\,AC = 12\,\,cm\).

a) Tính độ dài \(BC,\,\,AH\) và số đo \(\angle ACB\) (làm tròn đến phút)

b) Phân giác của \(\angle BAC\) cắt \(BC\) tại \(D\). Tính độ dài đoạn thẳng \(BD\).

Bài 6 (2,5 điểm): Từ một điểm \(A\) nằm ngoài đường tròn \(\left( {O;R} \right)\) với \(OA < 2R\). Vẽ hai tiếp tuyến \(AD,\,\,AE\) với đường tròn \(\left( O \right)\) (với \(D,\,\,E\) là các tiếp điểm).

a) Chứng minh tứ giác \(ADOE\) nội tiếp được đường tròn.

b) Lấy điểm \(M\) thuộc cung nhỏ \(DE\) (\(M\) khác \(D\), \(M\) khác \(E\), \(MD < ME\)). Tia \(AM\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai \(N\). Đoạn thẳng \(AO\) cắt cung nhỏ \(DE\) tại \(K\). Chứng minh \(NK\) là tia phân giác của \(\angle DNE\)

c) Kẻ đường kính \(KQ\) của \(\left( {O;R} \right)\). Tia \(QN\) cắt tia \(ED\) tại \(C\). Chứng minh \(MD.CE = ME.CD\).

Bài 7 (0,5 điểm):

Tìm tất cả các giá trị \(m\) là số nguyên sao cho giao điểm của đồ thị hai hàm số \(y = {m^2}x – 1\) và \(y =  – x + 2m\) có tọa độ là các số nguyên dương.

Đề bài

Bài 1:

Phương pháp:

Vận dụng hằng đẳng thức \(\sqrt {{A^2}}  = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,\,A \ge 0\\ – A\,\,\,khi\,\,\,A < 0\end{array} \right.\)

Thực hiện các phép toán với căn bậc hai

Cách giải:

Bài 2:

Phương pháp:

a) Phân tích đa thức thành nhân tử đưa phương trình về dạng tích \(A\left( x \right).B\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\) để giải phương trình hoặc sử dụng công thức nghiệm của phương trình bậc hai một ẩn số.

b) Phân tích đa thức thành nhân tử đưa phương trình về dạng tích \(A\left( x \right).B\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\) để giải phương trình.

c) Vận dụng phương pháp cộng đại số để tìm nghiệm của hệ phương trình.

d) Phương trình trùng phương nên đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\), phương trình đã cho trở thành phương trình bậc hai một ẩn số, giải phương trình này chọn được \(t\) và tìm được nghiệm của phương trình ban đầu.

Cách giải:

a) \({x^2} – 8x + 15 = 0\)

b) \(2{x^2} + 5x = 0\)

\(\begin{array}{l} \Leftrightarrow x\left( {2x + 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\2x + 5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  – \dfrac{5}{2}\end{array} \right.\end{array}\)

Vậy tập nghiệm của phương trình là \(S = \left\{ {0; – \dfrac{5}{2}} \right\}\).

c) \(\left\{ \begin{array}{l}2x + y = 5\\5x – 2y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x + 2y = 10\\5x – 2y = 8\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}9x = 18\\y = 5 – 2x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 5 – 2.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\)

Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {2;1} \right)\).

d) \(9{x^4} + 8{x^2} – 1 = 0\).

Đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\), phương trình đã cho trở thành \(9{t^2} + 8t – 1 = 0\) (*)

Ta có \(a – b + c = 9 – 8 – 1 = 0\) nên phương trình (*) có nghiệm \(t =  – 1\,\,\left( {ktm} \right)\) và \(t = \dfrac{1}{9}\,\,\left( {tm} \right)\).

Với \(t = \dfrac{1}{9} \Leftrightarrow {x^2} = \dfrac{1}{9} \Leftrightarrow x =  \pm \dfrac{1}{3}\).

Vậy tập nghiệm của phương trình là \(S = \left\{ { \pm \dfrac{1}{3}} \right\}\).

Bài 3:

Phương pháp:

a) Lập bảng giá trị tương ứng của \(x\) và \(y\) để vẽ đồ thị của parabol và đường thẳng.

b) Để phương trình đã cho có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) thì \(\Delta ‘ > 0\)

Khi đó áp dụng định lí Vi-ét, xác định được \({x_1} + {x_2};{x_1}.{x_2}\) sau đó thay vào phương trình để tìm tham số \(m\), đối chiếu điều kiện và kết luận.

Cách giải:

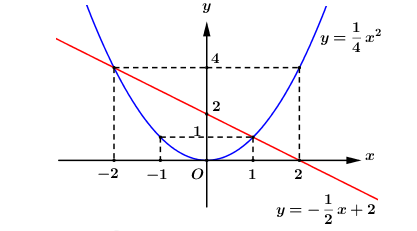
a) * \(\left( P \right):\,\,y = \dfrac{1}{4}{x^2}\) là parabol nhận trục \(Oy\) làm trục đối xứng và có bảng giá trị như sau:

\( \Rightarrow \) Parabol \(\left( P \right):\,\,y = \dfrac{1}{4}{x^2}\) đi qua các điểm \(\left( { – 4;4} \right),\,\,\left( { – 2;1} \right)\), \(\left( {0;0} \right),\,\,\left( {2;1} \right),\,\,\left( {4;4} \right)\).

* Đường thẳng \(\left( d \right):\,\,y =  – \dfrac{1}{2}x + 2\) có bảng giá trị như sau:

\( \Rightarrow \) Đường thẳng \(\left( d \right):\,\,y =  – \dfrac{1}{2}x + 2\)  đi qua điểm \(\left( {0;2} \right)\) và \(\left( {4;0} \right)\).

* Vẽ \(\left( P \right)\) và \(\left( d \right)\) trên cùng một mặt phẳng tọa độ.

b) Ta có: \(\Delta ‘ = {1^2} – \left( {m – 1} \right) = 1 – m + 1 = 2 – m\).

Để phương trình đã cho có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) thì \(\Delta ‘ > 0 \Leftrightarrow 2 – m > 0 \Leftrightarrow m < 2\,\,\left( * \right)\)

Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = m – 1\end{array} \right.\).

Ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,x_1^2 + x_2^2 – {x_1}{x_2} + x_1^2x_2^2 – 14 = 0\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} – 2{x_1}{x_2} – {x_1}{x_2} + x_1^2x_2^2 – 14 = 0\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} – 3{x_1}{x_2} + x_1^2x_2^2 – 14 = 0\\ \Leftrightarrow {2^2} – 3.\left( {m – 1} \right) + {\left( {m – 1} \right)^2} – 14 = 0\\ \Leftrightarrow 4 – 3m + 3 + {m^2} – 2m + 1 – 14 = 0\\ \Leftrightarrow {m^2} – 5m – 6 = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 6\\m =  – 1\end{array} \right.\end{array}\)

Đối chiếu điều kiện (*) ta thấy chỉ có \(m =  – 1\) thỏa mãn.

Vậy \(m =  – 1\).

Bài 4:

Phương pháp:

Giải bài toán bằng cách lập hệ phương trình, cụ thể gọi thời gian vòi một chảy một mình đầy bể là \(x\) (giờ), thời gian vòi hai chảy một mình đầy bể là \(y\) (giờ) (ĐK: \(x,y > 0\))

Tính được trong \(1\) giờ mỗi vào chạy được bao nhiêu phần của bể.

Lập được hệ phương trình và giải.

Cách giải:

Gọi thời gian vòi một chảy một mình đầy bể là \(x\) (giờ), thời gian vòi hai chảy một mình đầy bể là \(y\) (giờ)

(ĐK: \(x,y > 0\))

\( \Rightarrow \) Trong 1 giờ vòi một chảy được \(\dfrac{1}{x}\) bể và vòi hai chảy được \(\dfrac{1}{y}\) bể.

Vì 2 vòi cùng chảy thì trong 3 giờ đầy bể nên ta có phương trình \(\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{3}\,\,\,\left( 1 \right)\).

Trong \(20\) phút \( = \dfrac{1}{3}\) giờ vòi một chảy được \(\dfrac{1}{3}.\dfrac{1}{x} = \dfrac{1}{{3x}}\) (bể)

Trong \(30\) phút \( = \dfrac{1}{2}\) giờ tiếp theo vòi hai chảy được \(\dfrac{1}{2}.\dfrac{1}{y} = \dfrac{1}{{2y}}\) (bể)

Vì nếu mở vòi một chảy một mình trong 20 phút, rồi khóa lại, mở tiếp vòi hai chảy trong 30 phút thì cả hai vòi chảy được \(\dfrac{1}{8}\) bể nên ta có phương trình \(\dfrac{1}{{3x}} + \dfrac{1}{{2y}} = \dfrac{1}{8}\,\,\left( 2 \right)\)

Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{3}\\\dfrac{1}{{3x}} + \dfrac{1}{{2y}} = \dfrac{1}{8}\end{array} \right.\,\left( * \right)\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{3}\\\dfrac{8}{{24x}} + \dfrac{{12}}{{24y}} = \dfrac{3}{{24}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{3}\\\dfrac{8}{x} + \dfrac{{12}}{y} = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{8}{x} + \dfrac{8}{y} = \dfrac{8}{3}\\\dfrac{8}{x} + \dfrac{{12}}{y} = 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\dfrac{4}{y} = \dfrac{1}{3}\\\dfrac{1}{x} = \dfrac{1}{3} – \dfrac{1}{y}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 12\\\dfrac{1}{x} = \dfrac{1}{3} – \dfrac{1}{{12}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 12\\\dfrac{1}{x} = \dfrac{1}{4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 12\end{array} \right.\,\,\left( {tm} \right)\end{array}\)

Vậy thời gian vòi một chảy một mình đầy bể là \(4\) (giờ), thời gian vòi hai chảy một mình đầy bể là \(12\) (giờ).

Chú ý:

Khi giải hệ phương trình (*) học sinh có thể sử dụng phương pháp đặt ẩn phụ như sau:

Đặt \(u = \dfrac{1}{x},\,\,v = \dfrac{1}{y}\), hệ phương trình (*) trở thành

\(\begin{array}{l}\left\{ \begin{array}{l}u + v = \dfrac{1}{3}\\\dfrac{1}{3}u + \dfrac{1}{2}y = \dfrac{1}{8}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}u + v = \dfrac{1}{3}\\8u + 12v = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}8u + 8v = \dfrac{8}{3}\\8u + 12v = 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}4v = \dfrac{1}{3}\\u = \dfrac{1}{3} – v\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}v = \dfrac{1}{{12}}\\u = \dfrac{1}{4}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\dfrac{1}{y} = \dfrac{1}{{12}}\\\dfrac{1}{x} = \dfrac{1}{4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 12\\x = 4\end{array} \right.\end{array}\)

Bài 5:

Phương pháp:

a) Áp dụng định lí Pytago trong tam giác vuông \(ABC\), tính \(BC\)

Áp dụng hệ thức lượng trong tam giác vuông \(ABC\), tính \(AH\)

Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông, tính \(\tan \angle ACB \Rightarrow \angle ACB\)

b) Áp dụng định lí đường phân giác trong tam giác.

Cách giải:

a)

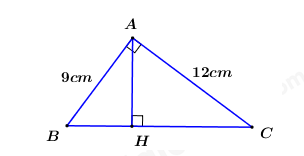
Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có:

\(\begin{array}{l}\,\,\,\,\,B{C^2} = A{B^2} + A{C^2}\\ \Rightarrow B{C^2} = {9^2} + {12^2}\\ \Rightarrow B{C^2} = 81 + 144\\ \Rightarrow B{C^2} = 225\\ \Rightarrow BC = \sqrt {225}  = 15\,\,\left( {cm} \right)\end{array}\)

Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) ta có:

\(\begin{array}{l}\,\,\,\,\,AH.BC = AB.AC\\ \Rightarrow AH = \dfrac{{AB.AC}}{{BC}}\\ \Rightarrow AH = \dfrac{{9.12}}{{15}} = 7,2\,\,\left( {cm} \right)\end{array}\)

Xét tam giác vuông \(ABC\) ta có:

\(\tan \angle ACB = \dfrac{{AB}}{{AC}} = \dfrac{9}{{12}} = \dfrac{3}{4}\)

\( \Rightarrow \angle ACB = \arctan \dfrac{3}{4} \approx {37^0}\).

Vậy \(BC = 15\,\,cm,\,\,AH = 7,2\,\,cm\) và \(\angle ACB \approx {37^0}\).

b)

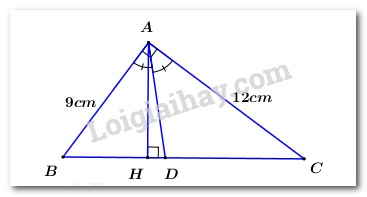
Áp dụng định lí đường phân giác ta có: \(\dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}} = \dfrac{9}{{12}} = \dfrac{3}{4}\).

\(\begin{array}{l} \Rightarrow \dfrac{{DB}}{{DB + DC}} = \dfrac{3}{{3 + 4}} \Rightarrow \dfrac{{DB}}{{BC}} = \dfrac{3}{7}\\ \Rightarrow DB = \dfrac{3}{7}BC = \dfrac{3}{7}.15 = \dfrac{{45}}{7}\,\,\left( {cm} \right)\end{array}\)

Vậy \(BD = \dfrac{{45}}{7}\,\,cm\).

Bài 6:

Phương pháp:

a) Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.

b) Vận dụng tính chất 2 tiếp tuyến cắt nhau và mối quan hệ của 2 góc nội tiếp chắn hai cung bằng nhau thì bằng nhau.

c) Chứng minh: \(\dfrac{{MD}}{{ND}} = \dfrac{{AD}}{{AN}}\), \(\dfrac{{ME}}{{NE}} = \dfrac{{AE}}{{AN}}\), \(AD = AE\) suy ra \(\dfrac{{MD}}{{ME}} = \dfrac{{ND}}{{NE}}\)

Chứng minh \(\dfrac{{ND}}{{NE}} = \dfrac{{CD}}{{CE}}\), từ đó chứng minh được \(MD.CE = ME.CD\).

Cách giải:

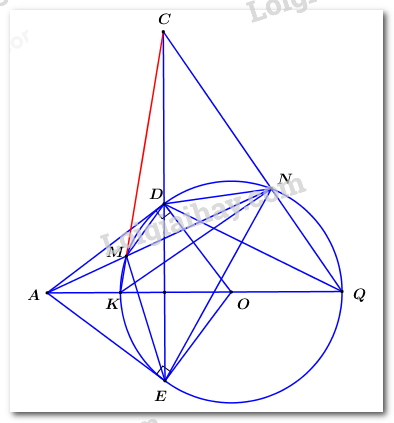
a) Vì \(AD,\,\,AE\) là các tiếp tuyến của đường tròn \(\left( O \right)\) lần lượt tại \(D,\,\,E\) nên \(\angle ODA = \angle OEA = {90^0}\) (định nghĩa)

Xét tứ giác \(ADOE\) có: \(\angle ODA + \angle OEA = {90^0} + {90^0} = {180^0}\) nên \(ADOE\) là tứ giác nội tiếp (dhnb).

b) Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có \(OA\) là tia phân giác của \(\angle DOE\).

\( \Rightarrow OK\) cũng là tia phân giác của \(\angle DOE\).

\( \Rightarrow \angle DOK = \angle EOK\).

\( \Rightarrow sdcDK = sdcEK\) (2 góc ở tâm bằng nhau thì chắn 2 cung bằng nhau).

\( \Rightarrow \angle DNK = \angle ENK\) (2 góc nội tiếp chắn hai cung bằng nhau thì bằng nhau)

Vậy \(NK\) là tia phân giác của \(\angle DNE\).

c) Xét \(\Delta AMD\) và \(\Delta ADN\) có:

\(\angle DAN\) chung;

\(\angle ADM = \angle AND\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(DM\))

\( \Rightarrow \Delta AMD \sim \Delta ADN\,\,\left( {g.g} \right)\)

\( \Rightarrow \dfrac{{MD}}{{ND}} = \dfrac{{AD}}{{AN}}\)   (1)

Xét \(\Delta AME\) và \(\Delta AEN\) có:

\(\angle EAN\) chung;

\(\angle AEM = \angle ANE\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(EM\))

\( \Rightarrow \Delta AME \sim AEN\,\,\left( {g.g} \right)\)

\( \Rightarrow \dfrac{{ME}}{{NE}} = \dfrac{{AE}}{{AN}}\)    (2)

Mà \(AD = AE\) (tính chất 2 tiếp tuyến cắt nhau)    (3)

Từ  (1), (2) và (3) \( \Rightarrow \dfrac{{MD}}{{ND}} = \dfrac{{ME}}{{NE}}\) \( \Rightarrow \dfrac{{MD}}{{ME}} = \dfrac{{ND}}{{NE}}\) (4).

Vì \(KQ\) là đường kính của \(\left( O \right)\,\,\,\left( {gt} \right)\) \( \Rightarrow \angle KNQ = {90^0}\) (góc nội tiếp chắn nửa đường tròn) hay \(NK \bot NQ\).

Theo ý b ta có \(NK\) là tia phân giác của \(\angle DNE\) \( \Rightarrow NQ\) là phân giác ngoài của \(\angle DNE\) hay \(NC\) là phân giác ngoài của \(\angle DNE\).

Áp dụng định lí đường phân giác ta có \(\dfrac{{ND}}{{NE}} = \dfrac{{CD}}{{CE}}\)  (5)

Từ (4) và (5) \( \Rightarrow \dfrac{{MD}}{{ME}} = \dfrac{{CD}}{{CE}} \Rightarrow MD.CE = ME.CD\) (đpcm).

Bài 7:

Phương pháp:

Xét phương trình hoành độ giao điểm của hai hàm số, tìm hoành độ giao điểm của hai hàm số đó sau đó tìm điêu kiện nguyên dương.

Cách giải:

Xét phương trình hoành độ giao điểm

\(\begin{array}{l}\,\,\,\,\,\,\,{m^2}x – 1 =  – x + 2m\\ \Leftrightarrow \left( {{m^2} + 1} \right)x = 2m + 1\\ \Leftrightarrow x = \dfrac{{2m + 1}}{{{m^2} + 1}}\,\left( {do\,\,{m^2} + 1 > 0\,\,\forall m} \right)\end{array}\)

Để giao điểm của 2 đồ thị có tọa độ nguyên dương thì \(\dfrac{{2m + 1}}{{{m^2} + 1}} \in {\mathbb{Z}^ + }\,\,\left( * \right)\).

Đặt \(\dfrac{{2m + 1}}{{{m^2} + 1}} = k\,\,\left( {k \in {\mathbb{Z}^ + }} \right)\) ta có

\(\begin{array}{l}\,\,\,\,\,\,\,2m + 1 = \left( {{m^2} + 1} \right)k\\ \Leftrightarrow 2m + 1 = k{m^2} + k\\ \Leftrightarrow k{m^2} – 2m + k – 1 = 0\,\,\,\left( 1 \right)\end{array}\)

Để tồn tại \(m\) thỏa mãn (*) thì phương trình (1) phải có nghiệm.

\(\begin{array}{l} \Rightarrow \Delta ‘ = 1 – k\left( {k – 1} \right) \ge 0\\ \Leftrightarrow  – {k^2} + k + 1 \ge 0\\ \Leftrightarrow \dfrac{{1 – \sqrt 5 }}{2} \le k \le \dfrac{{1 + \sqrt 5 }}{2}\end{array}\)

Mà \(k \in {\mathbb{Z}^ + } \Rightarrow k = 1\).

Khi đó ta có \(\dfrac{{2m + 1}}{{{m^2} + 1}} = 1 \Leftrightarrow {m^2} + 1 = 2m + 1 \Leftrightarrow {m^2} – 2m = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 2\end{array} \right.\).

Thử lại: Với \(m = 0 \Rightarrow x = \dfrac{{0 + 1}}{{{0^2} + 1}} = 1 \Rightarrow y =  – 1 + 2.0 =  – 1\) (ktm).

              Với \(m = 2\) \( \Rightarrow x = \dfrac{{2.2 + 1}}{{{2^2} + 1}} = 1 \Rightarrow y =  – 1 + 2.2 = 3\) ™.

Vậy có 1 giá trị \(m\) thỏa mãn yêu cầu bài toán là \(m = 2\).