1. Đề thi vào 10 môn Toán Phú Thọ năm 2023

Đề bài

Phần I: Trắc nghiệm (3 điểm)

Câu 1: Cho $\sqrt x {\rm{ \;}} = 6$, giá trị của $x$ bằng

A. 3

B. 12

C. 36

D. 6

Câu 2: Hàm số nào dưới đây là hàm số bậc nhất đồng biến trên $\mathbb{R}$ ?

A. $y = {\rm{ \;}} – 2x + 1$.

B. $y = 5x + 2$.

C. $y = {\rm{ \;}} – \frac{1}{3}x + 2$.

D. $y = {x^2}$.

Câu 3: Hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{x + y = 7}\\{2x – y = 11}\end{array}} \right.$ có nghiệm $\left( {x;y} \right)$ là

A. $\left( {6;1} \right)$.

B. $\left( { – 6; – 1} \right)$.

C. $\left( {1;6} \right)$.

D. $\left( {6; – 1} \right)$.

Câu 4: Điểm $M$ thuộc đồ thị hàm số $y = 3{x^2}$ và có hoành độ bằng 2 . Tung độ của điểm $M$ bằng

A. 12

B. 6

C. $\frac{4}{3}$

D. $\frac{2}{3}$

Câu 5: Cho phương trình ${x^2} – 2x – 5 = 0$ có hai nghiệm phân biệt ${x_1},{x_2}$. Giá trị của ${x_1} + {x_2}$ bằng

A. 5

B. 2.

C. -2

D. -5

Câu 6: Cho tam giác ABC vuông tại $A$ có $BC = 10$ và ${\rm{sin}}\angle ABC = \frac{3}{5}$. Độ dài cạnh AC bằng

A. 8

B. $\frac{{50}}{3}$

C. $\frac{{25}}{2}$

D. 6

Câu 7: Giá trị của tham số $m$ để đồ thị của các hàm số $y = 2x + 6$ và $y = 3x + m + 1$ cắt nhau tại một điềm trên trục tung bằng:

A. -10

B. -5

C. 5

D. 1

Câu 8: Có bao nhiêu giá trị của tham số $m$ để phương trình ${x^2} – 2mx + 4 = 0$ có nghiệm kép?

A. 1

B. 2

C. 3

D. 0

Câu 9: Cho tam giác ABC vuông tại $A$ có đường cao AH, biết $BH = 16$ và $HC = 9$. Độ dài cạnh AB bằng:

A. 16

B. 25

C. 20

D. 12

Câu 10: Từ một điểm $M$ nằm ngoài đường tròn $\left( {O;R} \right)$ và thỏa mãn $MO = 2R$, kẻ hai tiếp tuyến $MA,MB$ với đường tròn ( $A,B$ là hai tiếp điềm). Số đo góc $\angle AMB$ bằng

A. $30^\circ$.

B. $45^\circ$.

C. $75^\circ$.

D. $60^\circ$.

Câu 11: Một tổ công nhân theo kế hoạch phải sản xuất 140 sản phẩm trong thời gian nhất định, mỗi ngày sản xuất số sản phẩm như nhau. Thực tế mỗi ngày tổ công nhân làm thêm được 8 sản phẩm so với kế hoạch nên hoàn thành kế hoạch sớm hơn 2 ngày. Số sản phẩm phải sản xuất mỗi ngày theo kế hoạch của tổ công nhân là

A. 20

B. 14

C. 28

D. 10

Câu 12: Cho hai đường tròn $\left( {O;4} \right)$ và $\left( {O’;3} \right)$ cắt nhau tại hai điểm $A,B$. Gọi $AC,AD$ lần lượt là các đường kính của $\left( O \right)$ và $\left( {O’} \right)$ sao cho $AC,AD$ vuông góc với nhau như hình vẽ.

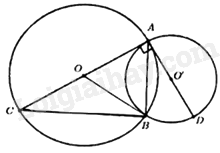
Độ dài $BC$ bằng

A. $\frac{{36}}{5}$.

B. $\frac{{16}}{5}$.

C. 6 .

D. $\frac{{32}}{5}$.

Phần II. Tự luận (7 điểm)

Câu 13: Cho hai biều thức $A = \frac{{5\sqrt a {\rm{ \;}} + 4}}{{\sqrt a {\rm{ \;}} – 1}}$ và $B = \left( {\frac{1}{{\sqrt a }} + \frac{1}{{1 – \sqrt a }}} \right) \cdot \frac{{\sqrt a {\rm{ \;}} – a}}{{\sqrt a {\rm{ \;}} – 2}}$, với $a > 0,a \ne 1,a \ne 4$

a) Tính giá trị của biểu thức $A$ khi $a = 16$.

b) Rút gọn biểu thức $B$.

c) Tìm các giá trị nguyên của $a$ để $A.B < 0$.

Câu 14: 

a) Cho parabol $\left( P \right):y = a{x^2}$. Tìm giá trị của $a$ để $\left( P \right)$ đi qua điểm $M\left( {1;2} \right)$. Với $a$ tìm được, tìm tọa độ các giao điểm của $\left( P \right)$ và đường thẳng $\left( d \right):y = 3x – 1$.

b) Cho hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{3x + y = 5m + 15}\\{x + y = 3m + 9}\end{array}} \right.$ có nghiệm $\left( {x;y} \right)$. Tìm giá trị của tham số $m$ để biểu thức $Q = xy – 2x – 1$ đạt giá trị nhỏ nhất.

Câu 15: Cho $\left( {O;R} \right)$ có hai đường kính $AB$ và $CD$ vuông góc với nhau. Lấy điểm $M$ trên cung nhỏ $AC$($M$ khác $A$ và $C$). Gọi $P,Q$ lần lượt là giao điểm của $AB$ với $MC$ và $MD$.

a) Chứng minh rằng tứ giác $OMPD$ nội tiếp.

b) Gọi $I,J$ lần lượt là giao điểm của $MB$ với $CA$ và $CD$. Chứng minh rằng $BJ.BM = 2{R^2}$.

c) Chứng minh rằng tam giác $AQI$ vuông cân.

d) Xác định vị trí điểm $M$ để tam giác $MQJ$ có diện tích lớn nhất.

Câu 16: Giải phương trình:  $8{x^2} – 13x + 11 = \frac{2}{x} + \left( {1 + \frac{3}{x}} \right)\sqrt[3]{{3{x^2} – 2}}$

—–HẾT—–

Lời giải chi tiết

Phần I: Trắc nghiệm

Câu 1 (NB):

Phương pháp:

Căn bậc hai số học của số a không âm là số x không âm, sao cho ${x^2} = a$

Cách giải:

$\sqrt x {\rm{ \;}} = 6 \Leftrightarrow x = {6^2} = 36$

Chọn C.

Câu 2 (NB):

Phương pháp:

Hàm số $y = ax + b(a \ne 0)$ đồng biến trên $\mathbb{R}$ khi a > 0.

Cách giải:

Hàm số $y = 5x + 2$ đồng biến trên $\mathbb{R}$

Chọn B.

Câu 3 (NB):

Phương pháp:

Giải hệ phương trình bằng phương pháp cộng đại số.

Cách giải:

$\left\{ {\begin{array}{*{20}{l}}{x + y = 7}\\{2x – y = 11}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x = 18}\\{y = 7 – x}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 6}\\{y = 7 – 6 = 1}\end{array}} \right.$

Hệ phương trình nghiệm $\left( {x;y} \right)$ là (6; 1)

Chọn A.

Câu 4 (NB):

Phương pháp:

Điểm $M({x_0};{y_0})$ thuộc đồ thị hàm số $y = a{x^2}(a \ne 0)$ thỏa mãn ${y_0} = a{x_0}^2$

Cách giải:

Điểm $M$ thuộc đồ thị hàm số $y = 3{x^2}$ và có hoành độ bằng 2 , tung độ là: $y = {3.2^2} = 12$

Chọn A.

Câu 5 (NB):

Phương pháp:

Hệ thức Vi-ét $\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ – b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.$

Cách giải:

Phương trình ${x^2} – 2x – 5 = 0$  có ${x_1} + {x_2} = \frac{{ – ( – 2)}}{1} = 2$

Chọn B.

Câu 6 (NB):

Phương pháp:

Tam giác ABC vuông tại $A$ có $\sin B = \frac{{AC}}{{BC}}$

Cách giải:

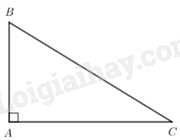
Tam giác ABC vuông tại $A$ có $\sin B = \frac{{AC}}{{BC}}$ $\Rightarrow \frac{3}{5} = \frac{{AC}}{{10}} \Rightarrow AC = \frac{{3.10}}{5} = 6$

Chọn D.

Câu 7 (TH):

Phương pháp:

Xét phương trình hoành độ giao điểm của hàm số $y = 2x + 6$ và $y = 3x + m + 1$, chúng cắt nhau tại một điềm trên trục tung thì x = 0

Cách giải:

Xét phương trình hoành độ giao điểm ta có:

$\begin{array}{*{20}{l}}{2x + 6 = 3x + m + 1}\\{ \Leftrightarrow 2x – 3x + 6 – 1 = m}\\{ \Leftrightarrow {\rm{\;}} – x + 5 = m}\end{array}$

Đề đồ thị của các hàm số $y = 2x + 6$ và $y = 3x + m + 1$ cắt nhau tại một điềm trên trục tung thì:

$– 0 + 5 = m \Leftrightarrow m = 5$

Chọn C.

Câu 8 (NB):

Phương pháp:

Công thức $\Delta {\rm{ \;}} = {(b’)^2} – ac$ với $b’ = \frac{b}{2}$

Điều kiện phương trình có nghiệm kép $\Delta {\rm{ \;}} = 0$

Cách giải:

Để phương trình ${x^2} – 2mx + 4 = 0$ có nghiệm kép: $\Delta ‘ = 0 \Rightarrow {( – m)^2} – 4 = 0 \Leftrightarrow {m^2} = 4 \Leftrightarrow m = {\rm{ \;}} \pm 2$

Có 2 giá trị của m thỏa mãn đề bài.

Chọn B.

Câu 9 (NB):

Phương pháp:

Hệ thức lượng trong tam giác ABC vuông tại $A$ có đường cao AH: $A{B^2} = BH.BC$

Cách giải:

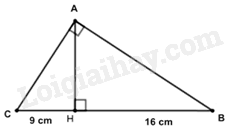
Hệ thức lượng trong tam giác ABC vuông tại $A$ có đường cao AH:

$A{B^2} = BH.BC \Rightarrow AB = \sqrt {BH.BC} {\rm{ \;}} = \sqrt {16.(16 + 9)} {\rm{ \;}} = 20$

Chọn C.

Câu 10 (TH):

Phương pháp:

Tính chất tiếp tuyến vuông góc với bán kính tại tiếp điểm. Tính chất hai tiếp tuyến cắt nhau.

Công thức lượng giác trong tam giác vuông.

Cách giải:

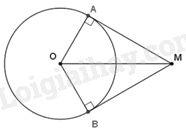
Vì MA, MB là tiếp tuyến cắt nhau tại M của (O) tại A, B

$\Rightarrow AM \bot OA;MO$ là phân giác của $\angle AMB$

Xét $\Delta OAM$ vuông tại A có: $\sin \angle AMO = \frac{{OA}}{{OM}} = \frac{R}{{2R}} = \frac{1}{2} \Rightarrow \angle AMO = 30^\circ$

Mà MO là phân giác của $\angle AMB$$\Rightarrow \angle AMB = 60^\circ$

Chọn D.

Câu 11 (VD):

Phương pháp:

Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.

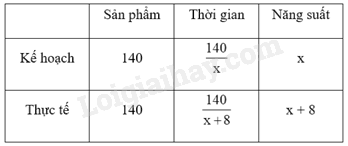
PT: Thực tế hoàn thành sớm hơn kế hoạch 2 ngày.

Cách giải:

Gọi số sản phẩm phải sản xuất mỗi ngày theo kế hoạch là x (sản phẩm).

Điều kiện $x \in N,x < 140$)

Theo kế hoạch, thời gian tổ sản suất trong $\frac{{140}}{x}$ (ngày)

Thực tế, mỗi ngày tổ sản suất được x + 8 (sản phẩm)

Thực tế, thời gian tổ sản suất trong $\frac{{140}}{{x + 8}}$ (ngày)

Vì thực tế hoàn thành sớm hơn kế hoạch 2 ngày nên ta có PT:

$\begin{array}{*{20}{l}}{\frac{{140}}{x} – \frac{{140}}{{x + 8}} = 2}\\{ \Leftrightarrow \frac{{70}}{x} – \frac{{70}}{{x + 8}} – 1 = 0}\\{ \Leftrightarrow 70(x + 8) – 70x – x(x + 8) = 0}\\{ \Leftrightarrow 70x + 560 – 70x – {x^2} – 8x = 0}\\{ \Leftrightarrow {\rm{ \;}} – {x^2} – 8x + 560 = 0}\\{ \Leftrightarrow {x^2} + 8x – 560 = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 20(TM)}\\{x = {\rm{ \;}} – 28(KTM)}\end{array}} \right.}\end{array}$

Vậy số sản phẩm phải sản xuất mỗi ngày theo kế hoạch của tổ công nhân là 20.

Chọn A.

Câu 12 (VDC):

Phương pháp:

Gọi H là trung điểm của AB.

Chứng minh được O, H, O’ thẳng hàng; C, B, D thẳng hàng.

Áp dụng tính chất đường kính đi qua trung điểm của dây (không đi qua tâm) thì vuông góc với dây đó.

Áp dụng định lí Pytago vào tam giác vuông.

Áp dụng hệ thức lượng trong tam giác vuông có đường cao.

Cách giải:

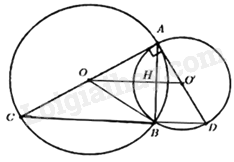
Gọi H là trung điểm của AB.

Áp dụng tính chất đường kính đi qua trung điểm của dây (không đi qua tâm) thì vuông góc với dây đó, ta có:

$OH \bot AB;O’H \bot AB \Rightarrow O,H,O’$ thẳng hàng

Dễ dàng chứng minh:

OH là đường trung bình $\Delta ABC \Rightarrow OH\parallel CB$ và HO’ là đường trung bình $\Delta ABD \Rightarrow HO’\parallel BD$

Mà O, H, O’ thẳng hàng suy ra C, B, D thẳng hàng.

Áp dụng định lí Pytago vào $\Delta ACD$ vuông tại A có:  $CD = \sqrt {A{C^2} + A{D^2}} {\rm{ \;}} = \sqrt {{{(4.2)}^2} + {{(3.2)}^2}} {\rm{ \;}} = 10$

Dễ dàng chứng minh OO’ là đường trung bình $\Delta ACD$ $\Rightarrow OO’ = \frac{{CD}}{2} = \frac{{10}}{2} = 5$

Áp dụng hệ thức lượng trong $\Delta AOO’$ vuông tại A có $AH \bot OO’$

$\begin{array}{*{20}{l}}{ \Rightarrow AH.OO’ = AO.AO’ \Rightarrow AH = \frac{{AO.AO’}}{{OO’}} = \frac{{4.3}}{5} = \frac{{12}}{5}}\\{ \Rightarrow AB = 2.AH = \frac{{24}}{5}}\end{array}$

Xét (O’) có AD là đường kính, B thuộc (O) $\Rightarrow \angle ABD = 90^\circ$ (góc nội tiếp chắn nửa đường tròn)

Áp dụng định lí Pytago vào $\Delta ABD$ vuông tại B có: $BD = \sqrt {A{D^2} – A{B^2}} {\rm{ \;}} = \sqrt {{{(3.2)}^2} – {{\left( {\frac{{24}}{5}} \right)}^2}} {\rm{ \;}} = \frac{{18}}{5}$

$\Rightarrow BC = CD – BD = 10 – \frac{{18}}{5} = \frac{{32}}{5}$

Chọn D.

Phần II: Tự luận

Câu 13 (TH):

Phương pháp:

a) Thay giá trị a (thỏa mãn điều kiện) vào biểu thức A.

b) Rút gọn biểu thức chứa căn bậc hai.

c) Giải bất phương trình.

Cách giải:

a) Với a = 16 (thoả mãn ĐKXĐ), thay vào biểu thức A ta được:

$A = \frac{{5\sqrt {16} {\rm{ \;}} + 4}}{{\sqrt {16} {\rm{ \;}} – 1}} = \frac{{5.4 + 4}}{{4 – 1}} = \frac{{24}}{3} = 8$.

Vậy khi a = 16 thì $A = 8$.

b) Với $a > 0,{\mkern 1mu} {\mkern 1mu} a \ne 1,{\mkern 1mu} {\mkern 1mu} a \ne 4$ ta có:

$\begin{array}{*{20}{l}}{B = \left( {\frac{1}{{\sqrt a }} + \frac{1}{{1 – \sqrt a }}} \right).\frac{{\sqrt a {\rm{ \;}} – a}}{{\sqrt a {\rm{ \;}} – 2}}}\\{B = \frac{{1 – \sqrt a {\rm{ \;}} + \sqrt a }}{{\sqrt a \left( {1 – \sqrt a } \right)}}.\frac{{\sqrt a \left( {1 – \sqrt a } \right)}}{{\sqrt a {\rm{ \;}} – 2}}}\\{B = \frac{1}{{\sqrt a \left( {1 – \sqrt a } \right)}}.\frac{{\sqrt a \left( {1 – \sqrt a } \right)}}{{\sqrt a {\rm{ \;}} – 2}}}\\{B = \frac{1}{{\sqrt a {\rm{ \;}} – 2}}}\end{array}$

Vậy với $a > 0,{\mkern 1mu} {\mkern 1mu} a \ne 1,{\mkern 1mu} {\mkern 1mu} a \ne 4$ thì $B = \frac{1}{{\sqrt a {\rm{ \;}} – 2}}$.

c) Ta có $A.B = \frac{{5\sqrt a {\rm{ \;}} + 4}}{{\sqrt a {\rm{ \;}} – 1}}.\frac{1}{{\sqrt a {\rm{ \;}} – 2}} = \frac{{5\sqrt a {\rm{ \;}} + 4}}{{\left( {\sqrt a {\rm{ \;}} – 1} \right)\left( {\sqrt a {\rm{ \;}} – 2} \right)}}$

Vì $5\sqrt a {\rm{ \;}} + 4 > 0{\mkern 1mu} {\mkern 1mu} \forall a$ nên $A.B < 0 \Leftrightarrow \left( {\sqrt a {\rm{ \;}} – 1} \right)\left( {\sqrt a {\rm{ \;}} – 2} \right) < 0$.

TH1: $\left\{ {\begin{array}{*{20}{l}}{\sqrt a {\rm{ \;}} – 1 < 0}\\{\sqrt a {\rm{ \;}} – 2 > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\sqrt a {\rm{ \;}} < 1}\\{\sqrt a {\rm{ \;}} > 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a < 1}\\{a > 4}\end{array}} \right.$ (Vô lí).

TH1: $\left\{ {\begin{array}{*{20}{l}}{\sqrt a {\rm{ \;}} – 1 > 0}\\{\sqrt a {\rm{ \;}} – 2 < 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\sqrt a {\rm{ \;}} > 1}\\{\sqrt a {\rm{ \;}} < 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a > 1}\\{a < 4}\end{array}} \right. \Rightarrow 1 < a < 4$.

Kết hợp điều kiện $a > 0,{\mkern 1mu} {\mkern 1mu} a \ne 1,{\mkern 1mu} {\mkern 1mu} a \ne 4$ ta có $1 < a < 4$.

Mà a là số nguyên nên $a \in \left\{ {2;3} \right\}$.

Vậy có 2 giá trị nguyên của a để A.B < 0 là a = 2 hoặc a = 3.

Câu 14 (VD):

Phương pháp:

a) Thay $M\left( {1;2} \right)$ vào hàm số $\left( P \right):y = a{x^2}$ tìm a.

Với a tìm được, xét phương trình hoành độ giao điểm của (P) và (d).

b) Giải hệ phương trình bằng phương pháp cộng đại số tìm (x; y).

Thay vào biểu thức tìm GTLN của biểu thức.

Cách giải:

a) Vì (P) đi qua điểm M(1;2) nên thay x = 1, y = 2 ta có: $2 = a{.1^2} \Leftrightarrow a = 2.$

Vậy để (P) đi qua M(1;2) thì a = 2.

Với a = 2 $\Rightarrow \left( P \right):{\mkern 1mu} {\mkern 1mu} y = 2{x^2}$.

Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình: $2{x^2} = 3x – 1 \Leftrightarrow 2{x^2} – 3x + 1 = 0$.

Ta có $a + b + c = 2 + \left( { – 3} \right) + 1 = 0$ nên phương trình có 2 nghiệm phân biệt $\left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = \frac{c}{a} = \frac{1}{2}}\end{array}} \right.$.

Với $x = 1 \Rightarrow y = {2.1^2} = 2 \Rightarrow A\left( {1;2} \right)$

Với $x = \frac{1}{2} \Rightarrow y = 2.{\left( {\frac{1}{2}} \right)^2} = \frac{1}{2} \Rightarrow B\left( {\frac{1}{2};\frac{1}{2}} \right)$.

Vậy với a = 2 thì toạ độ giao điểm của (P) và (d) là A(1;2) và $B\left( {\frac{1}{2};\frac{1}{2}} \right)$

b) $\left\{ {\begin{array}{*{20}{l}}{3x + y = 5m + 15}\\{x + y = 3m + 9}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2x = 2m + 6}\\{y = 3m + 9 – x}\end{array}} \right.$ $\Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = m + 3}\\{y = 3m + 9 – m – 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = m + 3}\\{y = 2m + 6}\end{array}} \right.$

$\begin{array}{*{20}{l}}{Q = xy – 2x – 1 = \left( {m + 3} \right)\left( {2m + 6} \right) – 2\left( {m + 3} \right) – 1}\\{ \Rightarrow Q = 2{{\left( {m + 3} \right)}^2} – 2\left( {m + 3} \right) – 1}\\{ \Rightarrow Q = 2\left[ {{{\left( {m + 3} \right)}^2} – 2\left( {m + 3} \right).\frac{1}{2} + \frac{1}{4}} \right] – \frac{3}{2}}\\{ \Rightarrow Q = 2{{\left[ {\left( {m + 3} \right) – \frac{1}{2}} \right]}^2} – \frac{3}{2}}\end{array}$

Do $2{\left[ {\left( {m + 3} \right) – \frac{1}{2}} \right]^2} \ge 0{\mkern 1mu} {\mkern 1mu} \forall m \Rightarrow 2{\left[ {\left( {m + 3} \right) – \frac{1}{2}} \right]^2} – \frac{3}{2} \ge {\rm{ \;}} – \frac{3}{2}$

$\Rightarrow Q \ge {\rm{ \;}} – \frac{3}{2}$.

Vậy giá trị nhỏ nhất của Q bằng $– \frac{3}{2}$, đạt được khi $m + 3 = 0 \Leftrightarrow m = {\rm{ \;}} – 3.$

Câu 15 (VD):

Phương pháp:

a) Chứng minh tứ giác OMPD có hai đỉnh kề nhau cùng nhìn một cạnh dưới một góc bằng nhau là tứ giác nội tiếp.

b) Chứng minh $\Delta BOJ \backsim \Delta BMA\left( {g.g} \right)$ suy ra các cạnh tỉ lệ.

c) Do đường kính AC, AB vuông góc với nhau nên số đo các cung AC, BC, BD, AD cùng bằng ${90^0}$

Sử dụng tính chất góc nội tiếp bằng nửa số đo cung bị chắn

Chứng minh tứ goác MIQA có hai đỉnh kề nhau cùng nhìn một cạnh dưới một góc bằng nhau là tứ giác nội tiếp.

Suy ra $\angle QAI = \angle QIA$ vì cùng bằng $\angle QMA = 45^\circ$

d) Sử dụng công thức diện tích ${S_{\Delta MQJ}} = \frac{1}{2}MQ.MJ.\sin \angle BMD$

Chứng minh $\Delta AMQ \backsim \Delta JMC\,\,\left( {g.g} \right)$$\Rightarrow MQ.MJ = MA.MC$

Để ${S_{\Delta MQJ}}{\mkern 1mu} {\mkern 1mu} \max {\rm{ \;}} \Leftrightarrow MA.MC{\mkern 1mu} {\mkern 1mu} \max {\rm{ \;}} \Rightarrow {S_{\Delta MAC}}{\mkern 1mu} {\mkern 1mu} \max$

Kẻ $MH \bot AC{\mkern 1mu} {\mkern 1mu} \left( {H \in AC} \right)$

Chứng minh AC không đổi.

$\Rightarrow {S_{\Delta MAC}}{\mkern 1mu} {\mkern 1mu} \max {\rm{ \;}} \Leftrightarrow M{H_{\max }} \Rightarrow M$ là điểm chính giữa của cung nhỏ AC.

Cách giải:

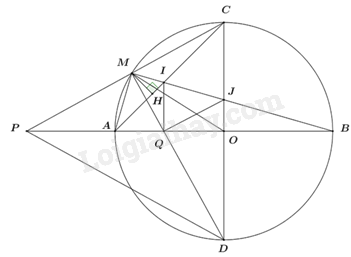
a) Ta có $\angle CMD = {90^0}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow \angle PMD = {90^0}$

Xét tứ giác OMPD có $\angle PMD = \angle POD = {90^0}$

Mà M, O là 2 đỉnh kề nhau cùng nhìn PD dưới 2 góc bằng nhau

Suy ra OMPD nội tiếp (dhnb)  (đpcm)

b) Ta có $\angle AMB = {90^0}$ (góc nội tiếp chắn nửa đường tròn)

Xét $\Delta BOJ$ và $\Delta BMA$ có: $\angle MBA$ chung và $\angle BOJ = \angle BMA\left( { = {{90}^0}} \right)$

$\Rightarrow \Delta BOJ \backsim \Delta BMA\left( {g.g} \right) \Rightarrow \frac{{BO}}{{BM}} = \frac{{BJ}}{{BA}}$ (cặp cạnh tương ứng tỉ lệ)

$\Rightarrow BJ.BM = BO.BA$

Mà $BO.BA = R.2R = 2{R^2}$ nên suy ra $BJ.BM = 2{R^2}$ (đpcm)

c) Do đường kính AC, AB vuông góc với nhau, nên số đo các cung AC, BC, BD, AD cùng bằng ${90^0}$

$\Rightarrow \angle DMB = \angle BAC = {45^0}$ (góc nội tiếp bằng nửa số đo cung bị chắn).

Xét tứ giác MIQA có $\angle QMI = \angle QAI{\mkern 1mu} {\mkern 1mu} \left( { = {{45}^0}} \right)$

Mà M, A là 2 đỉnh kề nhau cùng nhìn IQ dưới 2 góc bằng nhau

Suy ra MIQA nội tiếp (dhnb)

$\Rightarrow \angle AIQ = \angle AMQ = \frac{1}{2}sd{\mkern 1mu} {\mkern 1mu} cung{\mkern 1mu} AD = \frac{1}{2}{90^0} = {45^0}$

$\Rightarrow \Delta AIQ$ có $\angle AIQ = \angle IAQ = {45^0}$ nên tam giác AIQ vuông cân tại Q (đpcm).

d) Vì MIQA là tứ giác nội tiếp (cmt)

Nên $\angle MAQ = \angle QIJ$ (góc ngoài và góc trong tại đỉnh đối diện).

Mà $\left\{ {\begin{array}{*{20}{l}}{QI \bot AQ{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right)}\\{CO \bot AQ{\mkern 1mu} {\mkern 1mu} \left( {gt} \right)}\end{array}} \right. \Rightarrow QI//CO$ (từ vuông góc đến song song).

$\Rightarrow \angle QIJ = \angle MJC$ (so le trong).

$\Rightarrow \angle MAQ = \angle MJC$.

Vì $\left\{ {\begin{array}{*{20}{l}}{\angle CMJ = \frac{1}{2}{{.90}^0} = {{45}^0}}\\{\angle AMQ = \angle AMD = \frac{1}{2}{{.90}^0} = {{45}^0}}\end{array}} \right. \Rightarrow \angle CMJ = \angle AMQ$.

Xét $\Delta AMQ$ và $\Delta JMC$ có:

$\begin{array}{l}\angle MAQ = \angle MJC\,\,\left( {cmt} \right)\\\angle AMQ = \angle CMJ\,\,\left( {cmt} \right)\\ \Rightarrow \Delta AMQ \backsim \Delta JMC\,\,\left( {g.g} \right)\end{array}$

$\Rightarrow \frac{{MQ}}{{MC}} = \frac{{MA}}{{MJ}} \Rightarrow MQ.MJ = MA.MC$.

Ta có: ${S_{\Delta MQJ}} = \frac{1}{2}MQ.MJ.\sin \angle BMD = \frac{1}{2}MA.MC.\sin {45^0}$

$\Rightarrow {S_{\Delta MQJ}}{\mkern 1mu} {\mkern 1mu} \max {\rm{\;}} \Leftrightarrow MA.MC{\mkern 1mu} {\mkern 1mu} \max {\rm{\;}} \Rightarrow {S_{\Delta MAC}}{\mkern 1mu} {\mkern 1mu} \max$

Kẻ $MH \bot AC{\mkern 1mu} {\mkern 1mu} \left( {H \in AC} \right)$ ta có ${S_{\Delta MAC}} = \frac{1}{2}MH.AC$.

Áp dụng định lí Pythagore vào $\Delta OAC$ vuông tại O có: $A{C^2} = O{A^2} + O{C^2} = {R^2} + {R^2} = 2{R^2} \Rightarrow AC = R\sqrt 2$

=> AC không đổi.

$\Rightarrow {S_{\Delta MAC}}{\mkern 1mu} {\mkern 1mu} \max {\rm{\;}} \Leftrightarrow M{H_{\max }} \Rightarrow M$ là điểm chính giữa của cung nhỏ AC.

Vậy để diện tích tam giác MQJ lớn nhất thì M là điểm chính giữa của cung nhỏ AC.

Câu 16 (VDC):

Phương pháp:

Quy đồng, biến đổi, nhóm tạo hằng đẳng thức ${(a – b)^3}$

Đặt ẩn phụ, giải hệ phương trình.

Cách giải:

$\begin{array}{l}8{x^2} – 13x + 11 = \frac{2}{x} + \left( {1 + \frac{3}{x}} \right)\sqrt[3]{{3{x^2} – 2}}\\ \Leftrightarrow 8{x^3} – 13{x^2} + 11x – 2 = \left( {x + 3} \right)\sqrt[3]{{3{x^2} – 2}}\\ \Leftrightarrow 8{x^3} – 12{x^2} + 6x – 1 – {x^2} + 5x – 1 = \left( {x + 3} \right)\sqrt[3]{{2{x^2} – x + 6x – 3 + {x^2} – 5x + 1}}\\ \Leftrightarrow {\left( {2x – 1} \right)^3} – \left( {{x^2} – 5x + 1} \right) = \left( {x + 3} \right)\sqrt[3]{{\left( {2x – 1} \right)\left( {x + 3} \right) + {x^2} – 5x + 1}}\,\,\,\,\,\,\,(1)\end{array}$

Đặt: $\left\{ {\begin{array}{*{20}{l}}{u = 2x – 1}\\{v = \sqrt[3]{{\left( {2x – 1} \right)\left( {x + 3} \right) + {x^2} – 5x + 1}}}\end{array}} \right.$.

Khi đó ta có:

$\left\{ {\begin{array}{*{20}{l}}{{u^3} – \left( {{x^2} – 5x + 1} \right) = \left( {x + 3} \right)v}\\{{v^3} = u\left( {x + 3} \right) + {x^2} – 5x + 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{u^3} – \left( {{x^2} – 5x + 1} \right) = \left( {x + 3} \right)v{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 3 \right)}\\{{v^3} – \left( {{x^2} – 5x + 1} \right) = \left( {x + 3} \right)u{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 4 \right)}\end{array}} \right.$

Trừ 2 vế của (3) cho (4) ta được:

$\begin{array}{*{20}{l}}{{u^3} – {v^3} = \left( {x + 3} \right)\left( {v – u} \right)}\\{ \Leftrightarrow {u^3} – {v^3} + \left( {u – v} \right)\left( {x + 3} \right) = 0}\\{ \Leftrightarrow \left( {u – v} \right)\left( {{u^2} + uv + {v^2}} \right) + \left( {u – v} \right)\left( {x + 3} \right) = 0}\\{ \Leftrightarrow \left( {u – v} \right)\left( {{u^2} + uv + {v^2} + x + 3} \right) = 0{\mkern 1mu} {\mkern 1mu} \left( * \right)}\end{array}$

Vì ${u^2} + uv + {v^2} + x + 3 = {\left( {v + \frac{u}{2}} \right)^2} + \frac{{3{u^2}}}{4} + x + 3 \ge \frac{{3{u^2}}}{4} + x + 3$

$= \frac{3}{4}{\left( {2x – 1} \right)^2} + x + 3 = 3{x^2} – 3x + \frac{3}{4} + x + 3 = 3{x^2} – 2x + \frac{{15}}{4} = 3{\left( {x – \frac{1}{3}} \right)^2} + \frac{{41}}{{12}} > 0{\mkern 1mu} {\mkern 1mu} \forall x$

Do đó $\left( * \right) \Leftrightarrow$ $u = v$

$\begin{array}{l} \Rightarrow 2x – 1 = \sqrt[3]{{\left( {2x – 1} \right)\left( {x + 3} \right) + {x^2} – 5x + 1}}\\ \Leftrightarrow 2x – 1 = \sqrt[3]{{3{x^2} – 2}}\\ \Leftrightarrow 8{x^3} – 12{x^2} + 6x – 1 = 3{x^2} – 2\\ \Leftrightarrow 8{x^3} – 15{x^2} + 6x + 1 = 0\\ \Leftrightarrow 8{x^3} – 16{x^2} + 8x + {x^2} – 2x + 1 = 0\\ \Leftrightarrow 8x\left( {{x^2} – 2x + 1} \right) + {x^2} – 2x + 1 = 0\\ \Leftrightarrow \left( {8x + 1} \right)\left( {{x^2} – 2x + 1} \right) = 0\\ \Leftrightarrow \left( {8x + 1} \right){\left( {x – 1} \right)^2} = 0\\ \Leftrightarrow \left[ \begin{array}{l}8x + 1 = 0\\x – 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}8x =  – 1\\x – 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  – \frac{1}{8}\\x = 1\end{array} \right.\end{array}$

Vậy phương trình đã cho có tập nghiệm là: $S = \left\{ { – \frac{1}{8};1} \right\}$.