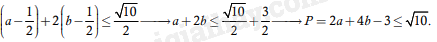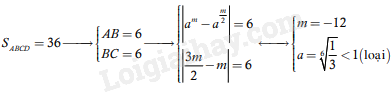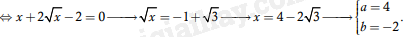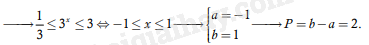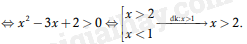A. NỘI DUNG ÔN TẬP
1. Một số yếu tố thống kê và xác suất
– Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm
– Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất
2. Hàm số mũ và hàm số logarit
– Phép tính lũy thừa với số mũ thực
– Phép tính logarit
– Hàm số mũ và hàm số logarit
– Phương trình, bất phương trình mũ và logarit
3. Đạo hàm
– Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm
– Các quy tắc tính đạo hàm
– Đạo hàm cấp hai
4. Quan hệ vuông góc trong không gian
– Hai đường thẳng vuông góc
– Đường thẳng vuông góc với mặt phẳng
– Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
– Hai mặt phẳng vuông góc
– Khoảng cách
– Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối
B. BÀI TẬP
Đề bài
I. Phần trắc nghiệm
1. Một số yếu tố thống kê và xác suất
Câu 1. Thời gian chạy 100m của 20 học sinh được ghi lại trong bảng dưới đây:

A. 17,015s
B. 17,015m
C. 17,1m
D. 17,1s
Câu 2. Có 100 học sinh tham dự kì thi học sinh giỏi Toán (thang điểm 20). Kết quả sau kì thi được thống kê như sau:

Tìm số điểm trung bình của 100 học sinh tham dự kì thi.
A. 15,22
B. 15,23
C. 15,24
D. 15,25
Câu 3. Cho bảng số liệu thống kê điểm kiểm tra giữa học kỳ I môn Toán của 40 học sinh như sau:

Số trung vị Me và mốt Mo của bảng số liệu trên lần lượt là:
A. Me=8,M0=40
B. Me=6,M0=18
C. Me=6,M0=6
D. Me=7,M0=6
Câu 4. Cho A,B là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?
A. P(A∪B)=P(A)+P(B)
B. P(A∪B)=P(A)⋅P(B)
C. P(A∪B)=P(A)–P(B)
D. P(A∩B)=P(A)+P(B)
Câu 5. A,B là hai biến cố độc lập. P(A)=0,5.P(A∩B)=0,2. Xác suất P(A∪B) bằng:
A. 0,3
B. 0,5
C. 0,6
D. 0,7
Câu 6. Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cố A : “ Mặt 3 chấm xuất hiện đúng một lần”.
A. P(A)=524
B. P(A)=532
C. P(A)=5324
D. P(A)=534
Câu 7. Một bài trắc nghiệm có 10 câu hỏi, mỗi câu hỏi có 4 phương án lựa chọn trong đó có 1 đáp án đúng. Giả sử mỗi câu trả lời đúng được 5 điểm và mỗi câu trả lời sai bị trừ đi 2 điểm. Một học sinh không học bài nên khoanh lụi một câu trả lời. Tìm xác suất để học sinh này nhận điểm dưới 1.
A. P(A)=0,7124
B. P(A)=0,7759
C. P(A)=0,7336
D. P(A)=0,783
Câu 8. Một người gọi điện thoại nhưng quên mất chữ số cuối. Tính xác suất để người đó gọi đúng số điện thoại mà không phải thử quá hai lần.
A. 15
B. 110
C. 1990
D. 29
2. Hàm số mũ và hàm số logarit
Câu 9. Tìm tập xác định D của hàm số y=log2(x2–2x–3)
A. D=(–∞;–1]∪[3;+∞)
B. D=[–1;3]
C. D=(–∞;–1)∪(3;+∞)
D. D=(–1;3)
Câu 10. Tìm tất cả các giá trị thực của tham số m để hàm số y=ln(x2–2mx+m) có tập xác định là R.
A. m<0
B. 0<m<1
C. m≤0; m≥1
D. 0≤m≤1
Câu 11. Hàm số nào sau đây đồng biến trên R?
A. y=(3π)x
B. y=(√2+√33)x
C. y=(√32)x
D. y=(π√2+√3)x
Câu 12. Cho a là một số thực dương khác 1 và các mệnh đề sau:
1) ax>0 với mọi x∈R.
2) Hàm số y=ax đồng biến trên R.
3) Hàm số y=e2017x là hàm số đồng biến trên R.
4) Đồ thị hàm số y=ax nhận trục Ox làm tiệm cận ngang.
Hỏi có bao nhiêu mệnh đề đúng?
A. 1
B. 2
C. 3
D. 4
Câu 13. Cho a là số thực tùy ý và b,c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số G, A(1;–1;–2) và y=xa,x>0. Khẳng định nào sau đây là đúng?
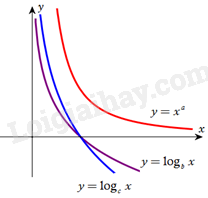
A. a<c<b.
B. a<b<c.
C. (43;–23;–83)
D. a>c>b.
Câu 14. Cho 9x+9–x=23. Tính giá trị biểu thức P=5+3x+3–x1–3x–3–x.
A. P=2.
B. P=32.
C. P=12.
D. P=–52.
Câu 15. Phương trình (5+2√6)3x+1=(5–2√6)5x+8có tích các nghiệm là?
A. –78
B. 4
C. –98
D. 18
Câu 16. Giải phương trình 2x–3=3x2–5x+6
A. S={2+log32;3}
B. S={log32;3}
C. S={2+log32}
D. S={2+log32;1}
Câu 17. Tập nghiệm của bất phương trình 22x<2x+6
A. (–∞;6)
B. (0;64)
C. (6;+∞)
D. (0;6)
Câu 18. Giải bất phương trình log2(3x–2)>log2(6–5x) được tập nghiệm là (a;b). Hãy tính tổng S=a+b.
A. S=265
B. S=115
C. S=2815
D. S=83
3. Đạo hàm
Câu 19. Cho hàm số f(x)={3–√4–x4khix≠014khix=0. Tính f′(0).
A. f′(0)=14.
B. f′(0)=116.
C. f′(0)=132.
D. Không tồn tại.
Câu 20. Một viên đạn được bắn lên cao theo phương trình s(t)=196t–4,9t2 trong đó t>0, t tính bằng giây kể từ thời điểm viên đạn được bắn lên cao và s(t) là khoảng cách của viên đạn so với mặt đất được tính bằng mét. Tại thời điểm vận tốc của viên đạn bằng 0 thì viên đạn cách mặt đất bao nhiêu mét?
A. 1690m.
B. 1069m.
C. 1906m.
D. 1960m.
Câu 21. Cho hàm số y=x3–3x2+2. Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm với đường thẳng y=–2.
A. y=–9x+7;y=–2.
B. y=–2.
C. y=9x+7;y=–2.
D. y=9x+7;y=2.
Câu 22. Tính đạo hàm của hàm số y=(x3–2x2)2016.
A. y′=2016(x3–2x2)2015.
B. y′=2016(x3–2x2)2015(3x2–4x).
C. y′=2016(x3–2x2)(3x2–4x).
D. y′=2016(x3–2x2)(3x2–2x).
Câu 23. Tính đạo hàm của hàm số y=x2+2x–3x+2.
A. y′=1+3(x+2)2.
B. y′=x2+6x+7(x+2)2.
C. y′=x2+4x+5(x+2)2.
D. y′=x2+8x+1(x+2)2.
Câu 24. Tính đạo hàm của hàm số f(x)=x√4–x2 tại điểm x=0.
A. f′(0)=12.
B. f′(0)=13.
C. f′(0)=1.
D. f′(0)=2.
Câu 25. Tính đạo hàm của hàm số y=cos3(2x–1).
A. y′=–3sin(4x–2)cos(2x–1).
B. y′=3cos2(2x–1)sin(2x–1).
C. y′=–3cos2(2x–1)sin(2x–1).
D. y′=6cos2(2x–1)sin(2x–1).
4. Quan hệ vuông góc trong không gian
Câu 26. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c khi b song song với c (hoặc b trùng vớic).
B. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c thì b song song với c.
C. Góc giữa hai đường thẳng là góc nhọn.
D. Góc giữa hai đường thẳng bằng góc giữa hai véctơ chỉ phương của hai đường thẳng đó.
Câu 27. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với đường thẳng còn lại.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Câu 28. Cho hình lập phương ABCD.A′B′C′D′. Góc giữa AC và DA′ là:
A. 450.
B. 900.
C. 600.
D. 1200.
Câu 29. Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD bằng
A. 600.
B. 300.
C. 900.
D. 450.
Câu 30. Cho hai đường thẳng a,b và mặt phẳng (P). Chỉ ra mệnh đề đúng trong các mệnh đề sau:
A. Nếu a⊥(P) và b⊥a thì b∥(P).
B. Nếu a∥(P) và b⊥(P) thì a⊥b.
C. Nếu a∥(P) và b⊥a thì b∥(P).
D. Nếu a∥(P) và b⊥a thì b⊥(P).
Câu 31. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O. Đường thẳng SA cuông góc với mặt đáy (ABCD). Gọi I là trung điểm của SC. Khẳng định nào dưới đây là sai?
A. IO⊥(ABCD).
B. BC⊥SB.
C. Tam giác SCD vuông ở D.
D. (SAC) là mặt phẳng trung trực của BD.
Câu 32. Cho hình chóp S.ABC có đá là tam giác đều cạnh và độ dài các cạnh bên Gọi là trọng tâm của tam giác Độ dài đoạn thẳng bằng
A. √9b2+3a23.
B. √b2−3a23.
C. √9b2−3a23.
D. √b2+3a23.
Câu 33. Cho hình vuông tâm cạnh bằng Trên đường thẳng qua và vuông góc với mặt phẳng lấy điểm Biết góc giữa đường thẳng và mặt phẳng bằng Độ dài cạnh bằng
A. SO=a√3.
B. SO=a√2.
C. SO=a√32.
D. SO=a√22.
Câu 34. Cho hình chóp có đáy là hình chữ nhật có cạnh , . Hai mặt bên và cùng vuông góc với mặt phẳng đáy , cạnh . Tính góc tạo bởi đường thẳng và mặt phẳng .
A. 300
B. 450
C. 600
D. 900
Câu 35. Cho hình chóp có đáy là tam giác vuông tại , , tam giác là tam giác đều có bằng cạnh và nằm trong mặt phẳng vuông với đáy. Gọi là góc giữa hai mặt phẳng và . Mệnh đề nào sau đây đúng?
A. φ=600.
B. tanφ=2√3.
C. tanφ=√36.
D. tanφ=12.
Câu 36. Cho hình chóp có đáy là tam giác đều cạnh . Cạnh bên và vuông góc với mặt đáy . Tính khoảng cách từ đến mặt phẳng .
A. d=a√155.
B. d=a.
C. d=a√55.
D. d=a√32.
Câu 37. Cho hình chóp có đáy là hình vuông cạnh , tâm . Cạnh bên và vuông góc với mặt đáy . Gọi và lần lượt là trung điểm của cạnh và . Tính khoảng cách giữa hai đường thẳng và .
A. a3.
B. 2a3.
C. 2a.
D. a2.
Câu 38. Cho hình hộp chữ nhật ABCD.A’B’C’D’ đáy là hình chữ nhật có AB = 2a, AD = 6a. Gọi M là trung điểm của AD, biết khoảng cách từ C đến mặt phẳng (A’BM) bằng . Thể tích khối hộp ABCD.A’B’C’D’ là
A. 24a3
B. 12a3
C. 3a3
D. 8a3
II. Phần tự luận
1. Một số yếu tố thống kê và xác suất
Câu 1. Tiền thưởng (đơn vị: triệu đồng) cho 43 cán bộ và nhân viên trong công ty X được thống kê lại như sau:

So sánh giá trị của các tứ phân vị Q1, Q2, Q3.
Câu 2. Tốc độ phát triển của một loại virus trong 10 ngày với các điều kiện khác nhau (đơn vị: nghìn con) được thống kê lại như sau:

Trong trường hợp này, ta nên chọn số nào dưới đây làm giá trị đại diện là tốt nhất? Tính giá trị đại diện đó.
Câu 3. Bảng thống kê năng suất trong một ngày sản xuất của một công ty cho bởi bảng số liệu sau đây:
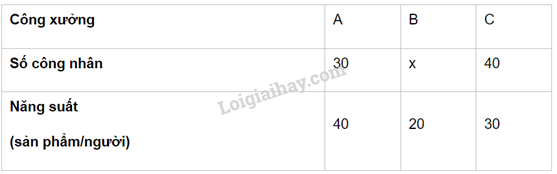
Công xưởng B và D mất số liệu về số công nhân mỗi công xưởng. Biết rằng tổng số công nhân của 2 xưởng đó là 80 và năng suất trung bình của công ty trong một ngày là 25 sản phẩm/người. Tìm x, y.
Câu 4. Trong kì thi thử THPT Quốc Gia, An làm để thi trắc nghiệm môn Toán. Đề thi gồm 50 câu hỏi, mỗi câu có 4 phương án trả lời, trong đó chỉ có một phương án đúng; trả lời đúng mỗi câu được 0,2 điểm. An trả lời hết các câu hỏi và chắc chắn đúng 45 câu, 5 câu còn lại An chọn ngẫu nhiên. Tính xác suất để điểm thi môn Toán của An không dưới 9, 5 điểm.
Câu 5. Có 3 chiếc hộp A,B,C. Hộp A chứa 4 bi đỏ, 3 bi trắng. Hộp B chứa 3 bi đỏ, 2 bi vàng. Hộp C chứa 2 bi đỏ, 2 bi vàng. Lấy ngẫu nhiên một hộp từ 3 hộp này, rồi lấy ngẫu nhiên một bi từ hộp đó. Tính xác suất để lấy được một bi đỏ.
Câu 6. Hai người ngang tài ngang sức tranh chức vô địch của một cuộc thi cờ tướng. Người giành chiến thắng là người đầu tiên thắng được năm ván cờ. Tại thời điểm người chơi thứ nhất đã thắng 4 ván và người chơi thứ hai mới thắng 2 ván, tính xác suất để người chơi thứ nhất giành chiến thắng.
Câu 7. Trong trận đấu bóng đá giữa 2 đội Real madrid và Barcelona, trọng tài cho đội Barcelona được hưởng một quả Penalty. Cầu thủ sút phạt ngẫu nhiên vào 1 trong bốn vị trí 1,2,3,4 và thủ môn bay người cản phá ngẫu nhiên đến 1 trong 4 vị trí 1, 2, 3, 4 với xác suất như nhau (thủ môn và cầu thủ sút phạt đều không đoán được ý định của đối phương). Biết nếu cầu thủ sút và thủ môn bay cùng vào vị trí 1 (hoặc 2 ) thì thủ môn cản phá được cú sút đó, nếu cùng vào vị trí 3 (hoặc 4 ) thì xác suất cản phá thành công là 50%. Tính xác suất của biến cố “cú sút đó không vào lưới”?

Câu 8. Tung một đồng xu không đồng chất 2020 lần. Biết rằng xác suất xuất hiện mặt sấp là 0,6. Tính xác suất để mặt sấp xuất hiện đúng 1010 lần
2. Hàm số mũ và hàm số logarit
Câu 9. Tìm tập xác định D của hàm số y=log2x–1x.
Câu 10. Tìm tất cả các giá trị thực của tham số m để hàm số y=log(x2–2x–m+1) có tập xác định là R.
Câu 11. Tìm tất cả các giá trị của tham số a để hàm số y=(a2–3a+3)x đồng biến
Câu 12. Cho a,b là các số thực thỏa mãn a2+b2>1 và loga2+b2a+b≥1. Tìm giá trị lớn nhất Pmax của biểu thức P=2a+4b–3.
Câu 13. Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có diện tích bằng 36, đường thẳng chứa cạnh AB song song với trục Ox, các đỉnh A,B và C lần lượt nằm trên đồ thị của các hàm số y=logax,y=log√ax và y=log3√ax với a là số thực lớn hơn 1. Tìm a.
Câu 14. Phương trình 4x2+x+21–x2=2(x+1)2+1 có tất cả bao nhiêu nghiệm?
Câu 15. Biết rằng phương trình 2log2x+log12(1–√x)=12log√2(x–2√x+2) có nghiệm duy nhất có dạng a+b√3 với a,b∈Z. Tính tổng S=a+b.
Câu 16. Gọi a,b lần lượt là nghiệm nhỏ nhất và nghiệm lớn nhất của bất phương trình 3.9x–10.3x+3≤0. Tính P=b–a.
Câu 17. Giải bất phương trình sau : log15(x2–1)<log15(3x–3).
Câu 18. Tìm m để phương trình :
a) 4x–m.2x+1+2m=0 có hai nghiệm thực x1,x2 thỏa mãn x1+x2=2.
b) 20172x–1–2m.2017x+m=0 có hai nghiệm thực x1,x2 thỏa mãn x1+x2=1.
3. Đạo hàm
Câu 19. Cho hàm số f(x) xác định trên R∖{2} bởi f(x)={x3–4x2+3xx2–3x+2khix≠10khix=1. Tính f′(1).
Câu 20. Tính đạo hàm của hàm số y=2x+5x2+3x+3.
Câu 21. Cho hàm số f(x)=k.3√x+√x. Với giá trị nào của k thì f′(1)=32?
Câu 22. Tính đạo hàm của hàm số y=cos(tanx).
Câu 23. Cho hàm số y=x.cosx. Tính giá trị biểu thức M=xy+xy”–2(y′–cosx).
4. Quan hệ vuông góc trong không gian
Câu 24. Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Tính số đo của góc (IJ,CD) ?
Câu 25. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, ^ABC=60∘, tam giác SBC là tam giác đều có cạnh bằng 2a và nằm trong mặt phẳng vuông với đáy. Tính góc giữa đường thẳng SA và mặt phẳng đáy (ABC)
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, BC=2a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Mặt phẳng (α) đi qua S vuông góc với AB. Tính diện tích S của thiết diện tạo bởi (α) với hình chóp đã cho?
Câu 27. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA=x và vuông góc với mặt phẳng (ABCD). Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau một góc 600.
Câu 28. Cho hình chóp S.ABC có tam giác ABC vuông tại B, AB=a√2,AC=a√3, cạnh bên SA vuông góc với mặt phẳng đáy và SB=a√3. Tính thể tích khối chóp S.ABC
——–Hết——–
Lời giải chi tiết
I. Trắc nghiệm
|
Câu 1. A
|
Câu 2. B
|
Câu 3. C
|
Câu 4. A
|
Câu 5. D
|
Câu 6.C
|
Câu 7. B
|
|
Câu 8. A
|
Câu 9. C
|
Câu 10. B
|
Câu 11.B
|
Câu 12. C
|
Câu 13. B
|
Câu 14. D
|
|
Câu 15. C
|
Câu 16. B
|
Câu 17. A
|
Câu 18. B
|
Câu 19. B
|
Câu 20. D
|
Câu 21. C
|
|
Câu 22. B
|
Câu 23. A
|
Câu 24. A
|
Câu 25. A
|
Câu 26. A
|
Câu 27. D
|
Câu 28. C
|
|
Câu 29. C
|
Câu 30. B
|
Câu 31. D
|
Câu 32. C
|
Câu 33. B
|
Câu 34. C
|
Câu 35. B
|
|
Câu 36. A
|
Câu 37. A
|
Câu 38. B
|
|
|
|
|
II. Phần tự luận
1. Một số yếu tố thống kê và xác suất
Câu 1. Tiền thưởng (đơn vị: triệu đồng) cho 43 cán bộ và nhân viên trong công ty X được thống kê lại như sau:

So sánh giá trị của các tứ phân vị Q1, Q2, Q3.
Phương pháp
Sử dụng công thức tính Q1, Q2, Q3
Lời giải chi tiết
Vì cỡ mẫu n = 43 = 2.21 + 1 là số lẻ, nên giá trị tứ phân vị thứ hai của mẫu số liệu là số liệu thứ 22.
Do đó giá trị tứ phân vị thứ hai Q2 = 4.
– Tứ phân vị thứ nhất là trung vị của nửa mẫu số liệu bên trái Q2 (không kể Q2).

Ta có cỡ mẫu lúc này n1 = 21 = 2.10 + 1 là số lẻ, nên giá trị tứ phân vị thứ nhất là số liệu thứ 11.
Do đó giá trị tứ phân vị thứ nhất Q1 = 3.
– Tứ phân vị thứ ba là trung vị của nửa mẫu số liệu bên phải Q2 (không kể Q2)

Ta có cỡ mẫu lúc này n2 = 21 = 2.10 + 1 là số lẻ, nên giá trị tứ phân vị thứ ba là số liệu thứ 11 của mẫu số liệu mới này.
Do đó giá trị tứ phân vị thứ ba Q3 = 5.
Vì 3 < 4 < 5 nên ta suy ra Q1 < Q2 < Q3
Câu 2. Tốc độ phát triển của một loại virus trong 10 ngày với các điều kiện khác nhau (đơn vị: nghìn con) được thống kê lại như sau:

Trong trường hợp này, ta nên chọn số nào dưới đây làm giá trị đại diện là tốt nhất? Tính giá trị đại diện đó.
Phương pháp
Sử dụng công thức tính giá trị đại diện
Lời giải chi tiết
Ta nên chọn số trung vị làm đại diện là tốt nhất vì có sự chênh lệch lớn giữa các số liệu trong mẫu. Do đó ta có thể loại đáp án A và B.
Sắp xếp mẫu dữ liệu trên theo thứ tự không giảm, ta được:
20; 20; 20; 30; 60; 100; 150; 270; 440; 980
Vì cỡ mẫu n = 10 = 2.5 nên trung vị của mẫu là trung bình cộng của số liệu thứ 5 và thứ 6.
Do đó Me = (60 + 100) : 2 = 80.
Câu 3. Bảng thống kê năng suất trong một ngày sản xuất của một công ty cho bởi bảng số liệu sau đây:
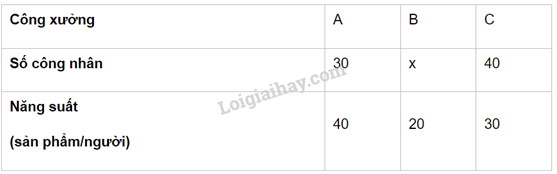
Công xưởng B và D mất số liệu về số công nhân mỗi công xưởng. Biết rằng tổng số công nhân của 2 xưởng đó là 80 và năng suất trung bình của công ty trong một ngày là 25 sản phẩm/người. Tìm x, y.
Phương pháp
Sử dụng công thức tính giá trị trung bình để tính năng suất trung bình.
Từ đó, lập hệ phương trình tìm x, y
Lời giải chi tiết
Ta có tổng số công nhân của 2 công xưởng B và D là 80 nên ta suy ra x + y = 80 (1).
Ta có năng suất trung bình của công ty trong một ngày là 25 sản phẩm/người.
Nên ta suy ra:
30.40+20x+40.30+15y30+x+40+y=25⇔2400+20x+15yx+y+70=25⇔20x+15y+2400=25x+25y+1750⇔5x+10y=650(2)
Từ (1) và (2) ta có hệ phương trình: {x+y=805x+10y=650⇔{x=30y=50
Giải hệ phương trình trên, ta được x = 30 và y = 50.
Câu 4. Trong kì thi thử THPT Quốc Gia, An làm để thi trắc nghiệm môn Toán. Đề thi gồm 50 câu hỏi, mỗi câu có 4 phương án trả lời, trong đó chỉ có một phương án đúng; trả lời đúng mỗi câu được 0,2 điểm. An trả lời hết các câu hỏi và chắc chắn đúng 45 câu, 5 câu còn lại An chọn ngẫu nhiên. Tính xác suất để điểm thi môn Toán của An không dưới 9, 5 điểm.
Phương pháp
Sử dụng quy tắc cộng xác suất
Lời giải chi tiết
Để An đúng được không dưới 9,5 điểm thì bạn ấy phải chọn đúng nhiều hơn 2 trong 5 câu còn lại.
Xác suất mỗi câu chọn đúng là 14 và không chọn đúng là 34.
Để An đúng được không dưới 9,5 điểm thì bạn ấy phải chọn đúng hoặc 3 hoặc 4 hoặc 5 trong 5 câu còn lại.
Do đó xác suất cần tìm là (14)3(34)2+(14)4(34)+(14)5=131024
Câu 5. Có 3 chiếc hộp A,B,C. Hộp A chứa 4 bi đỏ, 3 bi trắng. Hộp B chứa 3 bi đỏ, 2 bi vàng. Hộp C chứa 2 bi đỏ, 2 bi vàng. Lấy ngẫu nhiên một hộp từ 3 hộp này, rồi lấy ngẫu nhiên một bi từ hộp đó. Tính xác suất để lấy được một bi đỏ.
Phương pháp
Sử dụng quy tắc cộng xác suất
Lời giải chi tiết
Xác suất để chọn hộp A là 13, xác suất để chọn được bi đỏ trong hộp A là 47
⇒ Xác suất để chọn được bi đỏ trong hộp A là 13.47
Tương tự, xác suất để chọn được bi đỏ trong hộp B, hộp C lần lượt là 13.35+13.24
Vậy xác suất để lấy được bi đỏ là 13.47+13.35+13.24=3970
Câu 6. Hai người ngang tài ngang sức tranh chức vô địch của một cuộc thi cờ tướng. Người giành chiến thắng là người đầu tiên thắng được năm ván cờ. Tại thời điểm người chơi thứ nhất đã thắng 4 ván và người chơi thứ hai mới thắng 2 ván, tính xác suất để người chơi thứ nhất giành chiến thắng.
Phương pháp
Sử dụng quy tắc cộng xác suất
Lời giải chi tiết
Theo giả thiết hai người ngang tài ngang sức nên xác suất thắng thua trong một ván đấu là 0,5; 0,5.
Xét tại thời điểm người chơi thứ nhất đã thắng 4 ván và người chơi thứ hai thắng 2 ván.
Để người thứ nhất chiến thắng thì người thứ nhất cần thắng 1 ván và người thứ hai thắng không quá hai ván.
Có ba khả năng:
TH1: Đánh 1 ván. Người thứ nhất thắng xác suất là 0,5 .
TH2: Đánh 2 ván. Người thứ nhất thắng ở ván thứ hai xác suất là (0,5)2
TH3: Đánh 3 ván. Người thứ nhất thắng ở ván thứ ba xác suất là (0,5)3
Vậy P=0,5+(0,5)2+(0,5)3=78
Câu 7. Trong trận đấu bóng đá giữa 2 đội Real madrid và Barcelona, trọng tài cho đội Barcelona được hưởng một quả Penalty. Cầu thủ sút phạt ngẫu nhiên vào 1 trong bốn vị trí 1,2,3,4 và thủ môn bay người cản phá ngẫu nhiên đến 1 trong 4 vị trí 1, 2, 3, 4 với xác suất như nhau (thủ môn và cầu thủ sút phạt đều không đoán được ý định của đối phương). Biết nếu cầu thủ sút và thủ môn bay cùng vào vị trí 1 (hoặc 2 ) thì thủ môn cản phá được cú sút đó, nếu cùng vào vị trí 3 (hoặc 4 ) thì xác suất cản phá thành công là 50%. Tính xác suất của biến cố “cú sút đó không vào lưới”?

Phương pháp
Sử dụng quy tắc cộng xác suất và quy tắc nhân xác suất
Lời giải chi tiết
Gọi Ai là biến cố “cầu thủ sút phạt vào vị trí i ”
Bi là biến cố “thủ môn bay người cản phá vào vị trí thứ i ”
Và C là biến cố “Cú sút phạt không vào lưới”
Dễ thấy P(Ai)=P(Bi)=14
Ta có:
P(C)=P(A1).P(B1)+P(A2).P(B2)+12P(A3).P(B3)+12P(A4).P(B4)=(14)2+(14)2+12(14)2+12(14)2=316
Câu 8. Tung một đồng xu không đồng chất 2020 lần. Biết rằng xác suất xuất hiện mặt sấp là 0,6. Tính xác suất để mặt sấp xuất hiện đúng 1010 lần
Phương pháp
Sử dụng quy tắc cộng xác suất và quy tắc nhân xác suất
Lời giải chi tiết
Ta có C10102020 cách chọn 1010 vị trí trong 2020 lần tung đồng xu để mặt xấp xuất hiện, các lần tung còn lại không xuất hiện mặt sấp. Ửng với mỗi cách chọn cố định 1010 vị trí xuất hiện mặt xấp ta có xác suất của trường hợp đó tính như sau:
+) Tại những lần mặt xấp xuất hiện thì xác suất xảy ra là 0,6 .
+) Tại những lần mặt ngửa xuất hiện thì xác suất xảy ra là 1-0,6.
Do có 1010 lần xuất hiện mặt sấp và 1010 xuất hiện mặt ngữa nên ứng với mỗi cách chọn cố định 1010 vị trí xuất hiện mặt xấp thì có xác xuất là 0,61010.(1–0,6)1010=0,241010
Vậy xác suất cần tính là C10102020.0,241010
2. Hàm số mũ và hàm số logarit
Câu 9. Tìm tập xác định D của hàm số y=log2x–1x.
Phương pháp
Tập xác định của hàm số y=logaf(x)(0<a≠1) là
Lời giải chi tiết
Hàm số xác định ⇔x–1x>0⇔[x>1x<0
Vậy tập xác định của hàm số là (–∞;0)∪(1;+∞).
Đáp án D=(–∞;0)∪(1;+∞)
Câu 10. Tìm tất cả các giá trị thực của tham số m để hàm số y=log(x2–2x–m+1) có tập xác định là R.
Phương pháp
Hàm số y=ax2+bx+c(a≠0)>0∀x∈R⇔{a>0Δ<0
Lời giải chi tiết
Ycbt ⇔x2–2x–m+1>0,∀x∈R⇔{a>0Δ‘=1+m–1<0
⇔m<0
Câu 11. Tìm tất cả các giá trị của tham số a để hàm số y=(a2–3a+3)x đồng biến
Phương pháp
Hàm số y=ax đồng biến khi a>1, nghịch biến khi 0<a<1
Lời giải chi tiết
Hàm số đồng biến khi
a2–3a+3>1⇔a2–3a+2>0⇔[a<1a>2.
Câu 12. Cho a,b là các số thực thỏa mãn a2+b2>1 và loga2+b2a+b≥1. Tìm giá trị lớn nhất Pmax của biểu thức P=2a+4b–3.
Phương pháp
Sử dụng bất đẳng thức Bunhiacopxky
Lời giải chi tiết
Do a2+b2>1 nên loga2+b2(a+b)≥1⇔a+b≥a2+b2⇔(a–12)2+(b–12)2≤12 (1)
Ta có a+2b=[(a–12)+2(b–12)]+32. Áp dụng bất đẳng thức Bunhiacopxky ta có
[(a–12)+2(b–12)]2≤(12+22)[(a–12)2+(b–12)2]≤5.12=52.
Do đó:
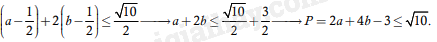
Dấu ”=” xảy ra ⇔a=5+√1010;b=5+2√1010.
Câu 13. Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có diện tích bằng 36, đường thẳng chứa cạnh AB song song với trục Ox, các đỉnh A,B và C lần lượt nằm trên đồ thị của các hàm số y=logax,y=log√ax và y=log3√ax với a là số thực lớn hơn 1. Tìm a.
Phương pháp
Lập phương trình diện tích ABCD để tìm m
Lời giải chi tiết
Do AB∥Ox→ A,B nằm trên đường thẳng y=m(m≠0).
Lại có A,B lần lượt nằm trên đồ thị của các hàm số y=logax,y=log√ax.
Từ đó suy ra A(am;m), B(am2;m).
Vì ABCD là hình vuông nên suy ra xC=xB=am2.
Lại có C nằm trên đồ thị hàm số y=log3√ax, suy ra C(am2;3m2).
Theo đề bài:
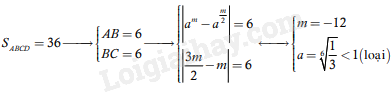
hoặc {m=12a=6√3.
Câu 14. Phương trình 4x2+x+21–x2=2(x+1)2+1 có tất cả bao nhiêu nghiệm?
Phương pháp
Đưa về cùng cơ số và đặt ẩn phụ
Lời giải chi tiết
Phương trình ⇔22x2+2x+21–x2=2x2+2x+1+1.
Đặt {a=22x2+2x>0b=21–x2>0, suy ra 2x2+2x+1=ab. Khi đó phương trình trở thành a+b=ab+1
⇔a–ab+b–1=0⇔a(1–b)+(b–1)=0⇔(1–b)(a–1)=0⇔[a=1b=1
Với a=1, ta được 22x2+2x=1⇔2x2+2x=0⇔[x=0x=–1
Với b=1, ta được 21–x2=1⇔1–x2=0⇔x=±1
Vậy phương trình đã cho có ba nghiệm x=0, x=±1
Câu 15. Biết rằng phương trình
2log2x+log12(1–√x)=12log√2(x–2√x+2) có nghiệm duy nhất có dạng a+b√3 với a,b∈Z. Tính tổng S=a+b.
Phương pháp
Đưa về cùng cơ số
Lời giải chi tiết
Điều kiện: 0<x<1.
Phương trình ⇔log2x2–log2(1–√x)=log2(x–2√x+2)
⇔log2x21–√x=log2(x–2√x+2)⇔x21–√x=x–2√x+2
⇔x21–√x=x+2(1–√x)⇔x2(1–√x)2=x1–√x+2⇔(x1–√x)2–(x1–√x)–2=0
⇔x1–√x=–1 (vô nghiệm) hoặc x1–√x=2
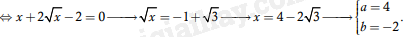
Vậy S=a+b=2
Câu 16. Gọi a,b lần lượt là nghiệm nhỏ nhất và nghiệm lớn nhất của bất phương trình 3.9x–10.3x+3≤0. Tính P=b–a.
Phương pháp
Đưa về cùng cơ số và đặt ẩn phụ, đưa về bất phương trình bậc hai ẩn t
Lời giải chi tiết
Bất phương trình tương đương với 3.32x–10.3x+3≤0.
Đặt t=3x, t>0. Bất phương trình trở thành 3t2–10t+3≤0⇔13≤t≤3.
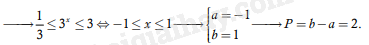
Câu 17. Giải bất phương trình sau : log15(x2–1)<log15(3x–3).
Phương pháp
Nếu 0 < a < 1 thì logaf(x)<logag(x)⇔f(x)>g(x)
Lời giải chi tiết
Điều kiện: {x2–1>03x–3>0⇔x>1.
Bất phương trình: log15(x2–1)<log15(3x–3)⇔x2–1>3x–3(chú ý với cơ số 15<1)
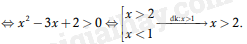
Câu 18. Tìm m để phương trình :
a) 4x–m.2x+1+2m=0 có hai nghiệm thực x1,x2 thỏa mãn x1+x2=2.
b) 20172x–1–2m.2017x+m=0 có hai nghiệm thực x1,x2 thỏa mãn x1+x2=1.
Phương pháp
Đặt ẩn phụ, đưa bài toán về tìm m để phương trình bậc hai có hai nghiệm dương phân biệt thỏa mãn yêu cầu bài toán
Lời giải chi tiết
a) Phương trình tương đương với (2x)2–2m.2x+2m=0.
Đặt t=2x>0, phương trình trở thành t2–2mt+2m=0. (∗)
Để phương trình đã cho có hai nghiệm ⇔ phương trình (∗) có hai nghiệm dương
⇔{Δ‘≥0S>0P>0⇔{m2–2m≥02m>02m>0⇔m≥2.
Theo định lí Viet, ta có:
2x1.2x2=2m⇔2x1+x2=2m⇔4=2m⇔m=2 (thỏa mãn).
b)Phương trình ⇔12017(2017x)2–2m.2017x+m=0
⇔(2017x)2–4034m.2017x+2017m=0.
Giả sử phương trình có hai nghiệm x1,x2.
Theo Viet, ta có: 2017x1.2017x2=2017m⇔2017x1+x2=2017m⇔2017=2017m⇔m=1.
Thử lại với m=1 ta thấy thỏa mãn
3. Đạo hàm
Câu 19. Cho hàm số f(x) xác định trên R∖{2} bởi f(x)={x3–4x2+3xx2–3x+2khix≠10khix=1. Tính f′(1).
Phương pháp
Sử dụng công thức tính đạo hàm theo định nghĩa
Lời giải chi tiết
Xét limx→1f(x)=limx→1x3–4x2+3xx2–3x+2=limx→1x(x–1)(x–3)(x–1)(x–2)=limx→1x(x–3)x–2=2.
Ta thấy: limx→1f(x)≠f(1). Do đó, hàm số không tiên tục tại điểm x=1.
Vậy hàm số không tồn tại đạo hàm tại điểm x=1.
Câu 20. Tính đạo hàm của hàm số y=2x+5x2+3x+3.
Phương pháp
Sử dụng công thức tính đạo hàm của hàm hợp
Lời giải chi tiết
Ta có y′=(2x+5)′(x2+3x+3)–(2x+5)(x2+3x+3)′(x2+3x+3)2
=2(x2+3x+3)–(2x+5)(2x+3)(x2+3x+3)2=–2x2–10x–9(x2+3x+3)2.
Câu 21. Cho hàm số f(x)=k.3√x+√x. Với giá trị nào của k thì f′(1)=32?
Phương pháp
Sử dụng công thức tính đạo hàm của hàm hợp
Lời giải chi tiết
Ta có (√u)′=u′2√u và (3√u)′=u′33√u2.
Do đó f′(x)=k33√x2+12√x→f′(1)=32⇔13k+12=32⇔13k=1⇔k=3.
Câu 22. Tính đạo hàm của hàm số y=cos(tanx).
Phương pháp
Sử dụng công thức tính đạo hàm của hàm hợp
Lời giải chi tiết
Ta có y′=–(tanx)′sin(tanx)=–1cos2x.sin(tanx)
Câu 23. Cho hàm số y=x.cosx. Tính giá trị biểu thức M=xy+xy”–2(y′–cosx).
Phương pháp
Sử dụng công thức tính đạo hàm của hàm hợp
Lời giải chi tiết
Ta có y′=cosx−x.sinx→y”=−2sinx−x.cosx.
Khi đó xy+xy”=x2cosx+x(–2sinx–xcosx)=–2xsinx.
Và 2(y′–cosx)=2(cosx–xsinx–cosx)=–2xsinx.
Vậy xy+xy”=2(y′–cosx)⇒M=0.
4. Quan hệ vuông góc trong không gian
Câu 24. Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Tính số đo của góc (IJ,CD) ?
Phương pháp
Kẻ đường thẳng cắt IJ và song song với CD
Lời giải chi tiết
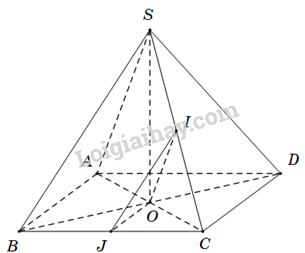
Gọi O là tâm của hình thoi ABCD⇒OJ là đường trung bình của ΔBCD.
Suy ra {OJ∥CDOJ=12CD.
Vì CD∥OJ⇒(IJ,CD)=(IJ,OJ).
Xét tam giác IOJ, có {IJ=12SB=a2OJ=12CD=a2IO=12SA=a2 ⇒ΔIOJ đều.
Vậy (IJ,CD)=(IJ,OJ)=^IJO=60∘
Câu 25. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, ^ABC=60∘, tam giác SBC là tam giác đều có cạnh bằng 2a và nằm trong mặt phẳng vuông với đáy. Tính góc giữa đường thẳng SA và mặt phẳng đáy (ABC)
Phương pháp
^(SA,(ABC))=^(SA,AH)=^SAH
Lời giải chi tiết
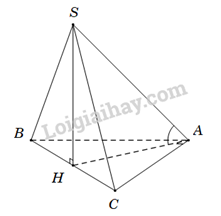
Gọi H là trung điểm của , suy ra SH⊥(ABC).
Vì SH⊥(ABC) nên HA là hình chiếu của SA trên mặt phẳng (ABC).
Do đó ^(SA,(ABC))=^(SA,AH)=^SAH.
Tam giác SBC đều cạnh 2a nên SH=a√3.
Tam giác ABC vuông tại A nên AH=12BC=a.
Tam giác vuông SAH, có tan^SAH=SHAH=√3, suy ra ^SAH=600.
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, BC=2a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Mặt phẳng (α) đi qua S vuông góc với AB. Tính diện tích S của thiết diện tạo bởi (α) với hình chóp đã cho
Phương pháp
Xác định thiết diện tạo bởi (α) với hình chóp
Thiết diện là tam giác vuông
Lời giải chi tiết
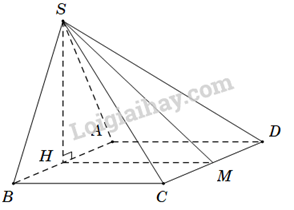
Gọi H là trung điểm AB⇒SH⊥AB. Suy ra:
SH⊂(α).
SH⊥(ABCD) (do (SAB)⊥(ABCD) theo giao tuyến AB).
Kẻ HM⊥AB(M∈CD)⇒HM⊂(α).
Do đó thiết diện là tam giác SHM vuông tại H.
Ta có SH=a√32, HM=BC=2a.
Vậy SΔSHM=12.a√32.2a=a2√32.
Câu 27. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA=x và vuông góc với mặt phẳng (ABCD). Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau một góc 600.
Phương pháp
Sử dụng phương pháp xác định góc giữa hai mặt phẳng
Lời giải chi tiết
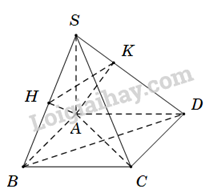
Từ A kẻ AH vuông góc với SB(H∈SB).
Ta có {SA⊥BCAB⊥BC⇒BC⊥(SAB)⇒BC⊥AH mà AH⊥SB suy ra AH⊥(SBC).
Từ A kẻ AK vuông góc với SD(K∈SD), tương tự, chứng minh được SK⊥(SCD).
Khi đó SC⊥(AHK) suy ra
^(SBC);(SCD)=^(AH;AK)=^HAK=600.
Lại có ΔSAB=ΔSAD⇒AH=AK mà ^HAK=600 suy ra tam giác AHK đều.
Tam giác SAB vuông tại S, có 1AH2=1SA2+1AB2⇒AH=xa√x2+a2.
Suy ra SH=√SA2–AH2=x2√x2+a2⇒SHSB=x2x2+a2.
Vì HK//BD suy ra
SHSB=HKBD⇔x2x2+a2=xa√x2+a2.a√2⇔x√x2+a2=1√2⇒x=a.
Câu 28. Cho hình chóp S.ABC có tam giác ABC vuông tại B, AB=a√2,AC=a√3, cạnh bên SA vuông góc với mặt phẳng đáy và SB=a√3. Tính thể tích khối chóp S.ABC
Phương pháp
Công thức tính thể tích chóp V=13h.SABC
Lời giải chi tiết
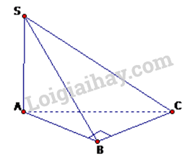
Tam giác ABC vuông tại B nên
BC=√AC2–AB2=a⇒SΔABC=12AB.BC=12a√2.a=a2√22
Tam giác SAB vuông tại A có SA=√SB2–AB2=a
Vậy thể tích khối chóp S.ABC là
VS.ABC=13SABC.SA=13a2√22a=a3√26
 HỌC NGAY
Môn Toán học Lớp 12SGK Toán lớp 12 SGK Toán 12 Nâng cao SBT Toán lớp 12 SBT Toán lớp 12 Nâng cao Đề thi, đề kiểm tra Toán lớp 12 SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diềuMôn Ngữ văn Lớp 12Soạn văn 12 siêu ngắn Soạn văn 12 chi tiết Tác giả – Tác phẩm lớp 12 Văn mẫu 12 Luyện dạng đọc hiểu Đề thi, đề kiểm tra Ngữ Văn 12 mới Bài tập trắc nghiệm Văn 12 Soạn văn – Kết nối tri thức Soạn văn – Cánh diều Xem thêmMôn Tiếng Anh Lớp 12Bài tập trắc nghiệm Tiếng Anh 12 mới Bài tập trắc nghiệm Tiếng Anh 12 Đề thi, đề kiểm tra Tiếng Anh 12 mới Tiếng Anh – Global Success Tiếng Anh – Friends Global Tiếng Anh – iLearn Smart World Tiếng Anh – Bright Tiếng Anh – English Discovery SGK Tiếng Anh 12 Mới Xem thêmMôn Vật lí Lớp 12SGK Vật lí lớp 12 SGK Vật lí lớp 12 Nâng cao SBT Vật lí lớp 12 Bài tập trắc nghiệm Lí 12 Đề thi, kiểm tra Lí lớp 12 SGK Vật Lí – Kết nối tri thức SGK Vật Lí – Cánh diều SGK Vật Lí – Chân trời sáng tạoMôn Hóa học Lớp 12SGK Hóa lớp 12 SGK Hóa học lớp 12 Nâng cao SBT Hóa lớp 12 Bài tập trắc nghiệm Hóa 12 Đề thi, đề kiểm tra Hóa lớp 12 SGK Hóa – Kết nối tri thức SGK Hóa – Cánh diều SGK Hóa – Chân trời sáng tạoMôn Sinh học Lớp 12SGK Sinh lớp 12 SGK Sinh lớp 12 Nâng cao SBT Sinh lớp 12 Bài tập trắc nghiệm Sinh 12 Đề thi, đề kiểm tra Sinh lớp 12 SGK Sinh – Kết nối tri thức SGK Sinh – Cánh diều SGK Sinh – Chân trời sáng tạoMôn Lịch sử Lớp 12Tập bản đồ Lịch sử lớp 12 Đề thi, đề kiểm tra Lịch sử 12 SGK Lịch sử lớp 12 SBT Lịch sử lớp 12Môn Địa lí Lớp 12SGK Địa lí lớp 12 SBT Địa lí lớp 12 Tập bản đồ Địa lí lớp 12 Đề thi, kiểm tra Địa lí lớp 12Môn GDCD Lớp 12SGK GDCDMôn Công nghệ Lớp 12SGK Công nghệ 12Môn Tin học Lớp 12SGK Tin học lớp 12
HỌC NGAY
Môn Toán học Lớp 12SGK Toán lớp 12 SGK Toán 12 Nâng cao SBT Toán lớp 12 SBT Toán lớp 12 Nâng cao Đề thi, đề kiểm tra Toán lớp 12 SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diềuMôn Ngữ văn Lớp 12Soạn văn 12 siêu ngắn Soạn văn 12 chi tiết Tác giả – Tác phẩm lớp 12 Văn mẫu 12 Luyện dạng đọc hiểu Đề thi, đề kiểm tra Ngữ Văn 12 mới Bài tập trắc nghiệm Văn 12 Soạn văn – Kết nối tri thức Soạn văn – Cánh diều Xem thêmMôn Tiếng Anh Lớp 12Bài tập trắc nghiệm Tiếng Anh 12 mới Bài tập trắc nghiệm Tiếng Anh 12 Đề thi, đề kiểm tra Tiếng Anh 12 mới Tiếng Anh – Global Success Tiếng Anh – Friends Global Tiếng Anh – iLearn Smart World Tiếng Anh – Bright Tiếng Anh – English Discovery SGK Tiếng Anh 12 Mới Xem thêmMôn Vật lí Lớp 12SGK Vật lí lớp 12 SGK Vật lí lớp 12 Nâng cao SBT Vật lí lớp 12 Bài tập trắc nghiệm Lí 12 Đề thi, kiểm tra Lí lớp 12 SGK Vật Lí – Kết nối tri thức SGK Vật Lí – Cánh diều SGK Vật Lí – Chân trời sáng tạoMôn Hóa học Lớp 12SGK Hóa lớp 12 SGK Hóa học lớp 12 Nâng cao SBT Hóa lớp 12 Bài tập trắc nghiệm Hóa 12 Đề thi, đề kiểm tra Hóa lớp 12 SGK Hóa – Kết nối tri thức SGK Hóa – Cánh diều SGK Hóa – Chân trời sáng tạoMôn Sinh học Lớp 12SGK Sinh lớp 12 SGK Sinh lớp 12 Nâng cao SBT Sinh lớp 12 Bài tập trắc nghiệm Sinh 12 Đề thi, đề kiểm tra Sinh lớp 12 SGK Sinh – Kết nối tri thức SGK Sinh – Cánh diều SGK Sinh – Chân trời sáng tạoMôn Lịch sử Lớp 12Tập bản đồ Lịch sử lớp 12 Đề thi, đề kiểm tra Lịch sử 12 SGK Lịch sử lớp 12 SBT Lịch sử lớp 12Môn Địa lí Lớp 12SGK Địa lí lớp 12 SBT Địa lí lớp 12 Tập bản đồ Địa lí lớp 12 Đề thi, kiểm tra Địa lí lớp 12Môn GDCD Lớp 12SGK GDCDMôn Công nghệ Lớp 12SGK Công nghệ 12Môn Tin học Lớp 12SGK Tin học lớp 12 HỌC NGAY
Môn Toán học Lớp 11SGK Toán – Kết nối tri thức SGK Toán – Cánh diều SGK Toán – Chân trời sáng tạo SGK Toán 11 – Cùng khám phá Chuyên đề học tập Toán – Kết nối tri thức Chuyên đề học tập Toán – Cánh diều Chuyên đề học tập Toán – Chân trời sáng tạo SBT Toán – Kết nối tri thức SBT Toán – Cánh diều Xem thêmMôn Ngữ văn Lớp 11Văn mẫu – Kết nối tri thức Văn mẫu – Cánh diều Văn mẫu – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Kết nối tri thức Đề thi, đề kiểm tra Văn – Cánh diều Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Tóm tắt, bố cục Văn – Kết nối tri thức Tóm tắt, bố cục Văn – Cánh diều Tóm tắt, bố cục Văn – Chân trời sáng tạo Xem thêmMôn Tiếng Anh Lớp 11Đề thi, đề kiểm tra Tiếng Anh – Bright Đề thi, đề kiểm tra Tiếng Anh – English Discovery SBT Tiếng Anh lớp 11 mới Đề thi, đề kiểm tra Tiếng Anh 11 mới Lý thuyết Tiếng Anh 11 Bài tập trắc nghiệm Tiếng Anh – Friends Global Bài tập trắc nghiệm Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Global Xem thêmMôn Vật lí Lớp 11SGK Vật Lí – Kết nối tri thức SGK Vật Lí – Cánh diều SGK Vật Lí – Chân trời sáng tạo Chuyên đề học tập Lí – Kết nối tri thức Chuyên đề học tập Lí – Cánh diều Chuyên đề học tập Lí – Chân trời sáng tạo SBT Vật lí – Kết nối tri thức SBT Vật lí – Cánh diều SBT Vật lí – Chân trời sáng tạo Xem thêmMôn Hóa học Lớp 11SBT Hóa – Chân trời sáng tạo Lý thuyết Hóa 11 Đề thi, kiểm tra Hóa – Kết nối tri thức Đề thi, kiểm tra Hóa – Cánh diều Đề thi, kiểm tra Hóa – Chân trời sáng tạo Bài tập trắc nghiệm Hóa – Kết nối tri thức Bài tập trắc nghiệm Hóa – Cánh diều Bài tập trắc nghiệm Hóa – Chân trời sáng tạo SGK Hóa học – Kết nối tri thức Xem thêmMôn Sinh học Lớp 11SGK Sinh – Kết nối tri thức SGK Sinh – Cánh diều SGK Sinh – Chân trời sáng tạo Chuyên đề học tập Sinh – Kết nối tri thức Chuyên đề học tập Sinh – Cánh diều Chuyên đề học tập Sinh – Chân trời sáng tạo SBT Sinh – Kết nối tri thức SBT Sinh – Cánh diều SBT Sinh – Chân trời sáng tạo Xem thêmMôn Lịch sử Lớp 11SGK Lịch sử – Kết nối tri thức SGK Lịch sử – Chân trời sáng tạo SGK Lịch sử – Cánh diều Đề thi, kiểm tra Lịch sử lớp 11Môn Địa lí Lớp 11SGK Địa lí – Kết nối tri thức SGK Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Địa lí lớp 11 SGK Địa lí – Cánh diềuMôn GD kinh tế và pháp luật Lớp 11SGK Giáo dục kinh tế và pháp luật – Kết nối tri thức SGK Giáo dục kinh tế và pháp luật – Chân trời sáng tạo SGK Giáo dục kinh tế và pháp luật – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 11SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 11SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diềuMôn GD Quốc phòng và An ninh Lớp 11SGK Giáo dục quốc phòng và an ninh – Kết nối tri thức SGK Giáo dục quốc phòng và an ninh – Cánh diều
HỌC NGAY
Môn Toán học Lớp 11SGK Toán – Kết nối tri thức SGK Toán – Cánh diều SGK Toán – Chân trời sáng tạo SGK Toán 11 – Cùng khám phá Chuyên đề học tập Toán – Kết nối tri thức Chuyên đề học tập Toán – Cánh diều Chuyên đề học tập Toán – Chân trời sáng tạo SBT Toán – Kết nối tri thức SBT Toán – Cánh diều Xem thêmMôn Ngữ văn Lớp 11Văn mẫu – Kết nối tri thức Văn mẫu – Cánh diều Văn mẫu – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Kết nối tri thức Đề thi, đề kiểm tra Văn – Cánh diều Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Tóm tắt, bố cục Văn – Kết nối tri thức Tóm tắt, bố cục Văn – Cánh diều Tóm tắt, bố cục Văn – Chân trời sáng tạo Xem thêmMôn Tiếng Anh Lớp 11Đề thi, đề kiểm tra Tiếng Anh – Bright Đề thi, đề kiểm tra Tiếng Anh – English Discovery SBT Tiếng Anh lớp 11 mới Đề thi, đề kiểm tra Tiếng Anh 11 mới Lý thuyết Tiếng Anh 11 Bài tập trắc nghiệm Tiếng Anh – Friends Global Bài tập trắc nghiệm Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Global Xem thêmMôn Vật lí Lớp 11SGK Vật Lí – Kết nối tri thức SGK Vật Lí – Cánh diều SGK Vật Lí – Chân trời sáng tạo Chuyên đề học tập Lí – Kết nối tri thức Chuyên đề học tập Lí – Cánh diều Chuyên đề học tập Lí – Chân trời sáng tạo SBT Vật lí – Kết nối tri thức SBT Vật lí – Cánh diều SBT Vật lí – Chân trời sáng tạo Xem thêmMôn Hóa học Lớp 11SBT Hóa – Chân trời sáng tạo Lý thuyết Hóa 11 Đề thi, kiểm tra Hóa – Kết nối tri thức Đề thi, kiểm tra Hóa – Cánh diều Đề thi, kiểm tra Hóa – Chân trời sáng tạo Bài tập trắc nghiệm Hóa – Kết nối tri thức Bài tập trắc nghiệm Hóa – Cánh diều Bài tập trắc nghiệm Hóa – Chân trời sáng tạo SGK Hóa học – Kết nối tri thức Xem thêmMôn Sinh học Lớp 11SGK Sinh – Kết nối tri thức SGK Sinh – Cánh diều SGK Sinh – Chân trời sáng tạo Chuyên đề học tập Sinh – Kết nối tri thức Chuyên đề học tập Sinh – Cánh diều Chuyên đề học tập Sinh – Chân trời sáng tạo SBT Sinh – Kết nối tri thức SBT Sinh – Cánh diều SBT Sinh – Chân trời sáng tạo Xem thêmMôn Lịch sử Lớp 11SGK Lịch sử – Kết nối tri thức SGK Lịch sử – Chân trời sáng tạo SGK Lịch sử – Cánh diều Đề thi, kiểm tra Lịch sử lớp 11Môn Địa lí Lớp 11SGK Địa lí – Kết nối tri thức SGK Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Địa lí lớp 11 SGK Địa lí – Cánh diềuMôn GD kinh tế và pháp luật Lớp 11SGK Giáo dục kinh tế và pháp luật – Kết nối tri thức SGK Giáo dục kinh tế và pháp luật – Chân trời sáng tạo SGK Giáo dục kinh tế và pháp luật – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 11SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 11SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diềuMôn GD Quốc phòng và An ninh Lớp 11SGK Giáo dục quốc phòng và an ninh – Kết nối tri thức SGK Giáo dục quốc phòng và an ninh – Cánh diều HỌC NGAY
Môn Toán học Lớp 10SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Chuyên đề học tập Toán – Kết nối tri thức Chuyên đề học tập Toán – Chân trời sáng tạo Chuyên đề học tập Toán – Cánh diều Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Lý thuyết Toán 10 Xem thêmMôn Ngữ văn Lớp 10Soạn văn – Kết nối tri thức – siêu ngắn Đề thi, đề kiểm tra Văn – Kết nối tri thức Soạn văn – Kết nối tri thức – chi tiết Đề thi, đề kiểm tra Văn – Cánh diều Soạn văn – Chân trời sáng tạo – siêu ngắn Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Soạn văn – Chân trời sáng tạo – chi tiết Lý thuyết Văn 10 Soạn văn – Cánh Diều – siêu ngắn Xem thêmMôn Tiếng Anh Lớp 10Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Tiếng Anh – Friends Global Đề thi, đề kiểm tra Tiếng Anh – Bright Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – English Discovery Tiếng Anh – English Discovery Lý thuyết Tiếng Anh 10 Tiếng Anh – Bright Xem thêmMôn Vật lí Lớp 10SBT Vật lí – Chân trời sáng tạo SBT Vật lí – Cánh diều Bài tập trắc nghiệm Lí – Kết nối tri thức Bài tập trắc nghiệm Lí – Chân trời sáng tạo Bài tập trắc nghiệm Lí – Cánh diều Đề thi, đề kiểm tra Vật lí – Chân trời sáng tạo Đề thi, đề kiểm tra Vật lí – Kết nối tri thức Đề thi, đề kiểm tra Vật lí – Cánh diều Chuyên đề học tập Lí – Kết nối tri thức Xem thêmMôn Hóa học Lớp 10SGK Hóa – Kết nối tri thức SGK Hóa – Chân trời sáng tạo SGK Hóa – Cánh diều SBT Hóa – Kết nối tri thức SBT Hóa – Chân trời sáng tạo SBT Hóa 10 – Cánh diều Chuyên đề học tập Hóa – Kết nối tri thức Chuyên đề học tập Hóa 10 – Chân trời sáng tạo Chuyên đề học tập Hóa 10 – Cánh diều Xem thêmMôn Sinh học Lớp 10SBT Sinh – Chân trời sáng tạo SBT Sinh – Cánh diều Chuyên đề học tập Sinh – Kết nối tri thức Chuyên đề học tập Sinh – Chân trời sáng tạo Bài tập trắc nghiệm Sinh – Kết nối tri thức Bài tập trắc nghiệm Sinh – Chân trời sáng tạo Bài tập trắc nghiệm Sinh – Cánh diều Đề thi, kiểm tra Sinh – Kết nối tri thức Đề thi, kiểm tra Sinh – Chân trời sáng tạo Xem thêmMôn Lịch sử Lớp 10SGK Lịch sử – Kết nối tri thức SGK Lịch sử – Chân trời sáng tạo SGK Lịch sử – Cánh Diều SBT Lịch sử – Kết nối tri thức SBT Lịch sử – Chân trời sáng tạo SBT Lịch sử – Cánh Diều Chuyên đề học tập Lịch sử – Kết nối tri thức Đề thi, đề kiểm tra Lịch sử – Kết nối tri thức Đề thi, đề kiểm tra Lịch sử lớp 10 – Chân trời sáng tạo Xem thêmMôn Địa lí Lớp 10SGK Địa lí – Kết nối tri thức SGK Địa lí – Cánh Diều SGK Địa lí – Chân trời sáng tạo SBT Địa lí – Kết nối tri thức SBT Địa lí – Chân trời sáng tạo Đề thi, đề kiểm tra Địa lí – Kết nối tri thức Đề thi, đề kiểm tra Địa lí lớp 10 – Chân trời sáng tạo Đề thi, đề kiểm tra Địa lí – Kết nối tri thứcMôn GDCD Lớp 10SGK Giáo dục kinh tế và pháp luật – KNTT SGK Giáo dục kinh tế và pháp luật – CTST SGK Giáo dục kinh tế và pháp luật – Cánh diềuMôn Tin học Lớp 10SGK Tin học – Kết nối tri thức SGK Tin học – Cánh Diều SBT Tin học – Kết nối tri thứcMôn HĐ trải nghiệm, hướng nghiệp Lớp 10SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh DiềuMôn Giáo dục thể chất Lớp 10SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diềuMôn GD Quốc phòng và An ninh Lớp 10SGK Giáo dục quốc phòng và an ninh – Kết nối tri thức SGK Giáo dục quốc phòng và an ninh – Cánh diều
HỌC NGAY
Môn Toán học Lớp 10SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Chuyên đề học tập Toán – Kết nối tri thức Chuyên đề học tập Toán – Chân trời sáng tạo Chuyên đề học tập Toán – Cánh diều Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Lý thuyết Toán 10 Xem thêmMôn Ngữ văn Lớp 10Soạn văn – Kết nối tri thức – siêu ngắn Đề thi, đề kiểm tra Văn – Kết nối tri thức Soạn văn – Kết nối tri thức – chi tiết Đề thi, đề kiểm tra Văn – Cánh diều Soạn văn – Chân trời sáng tạo – siêu ngắn Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Soạn văn – Chân trời sáng tạo – chi tiết Lý thuyết Văn 10 Soạn văn – Cánh Diều – siêu ngắn Xem thêmMôn Tiếng Anh Lớp 10Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Tiếng Anh – Friends Global Đề thi, đề kiểm tra Tiếng Anh – Bright Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – English Discovery Tiếng Anh – English Discovery Lý thuyết Tiếng Anh 10 Tiếng Anh – Bright Xem thêmMôn Vật lí Lớp 10SBT Vật lí – Chân trời sáng tạo SBT Vật lí – Cánh diều Bài tập trắc nghiệm Lí – Kết nối tri thức Bài tập trắc nghiệm Lí – Chân trời sáng tạo Bài tập trắc nghiệm Lí – Cánh diều Đề thi, đề kiểm tra Vật lí – Chân trời sáng tạo Đề thi, đề kiểm tra Vật lí – Kết nối tri thức Đề thi, đề kiểm tra Vật lí – Cánh diều Chuyên đề học tập Lí – Kết nối tri thức Xem thêmMôn Hóa học Lớp 10SGK Hóa – Kết nối tri thức SGK Hóa – Chân trời sáng tạo SGK Hóa – Cánh diều SBT Hóa – Kết nối tri thức SBT Hóa – Chân trời sáng tạo SBT Hóa 10 – Cánh diều Chuyên đề học tập Hóa – Kết nối tri thức Chuyên đề học tập Hóa 10 – Chân trời sáng tạo Chuyên đề học tập Hóa 10 – Cánh diều Xem thêmMôn Sinh học Lớp 10SBT Sinh – Chân trời sáng tạo SBT Sinh – Cánh diều Chuyên đề học tập Sinh – Kết nối tri thức Chuyên đề học tập Sinh – Chân trời sáng tạo Bài tập trắc nghiệm Sinh – Kết nối tri thức Bài tập trắc nghiệm Sinh – Chân trời sáng tạo Bài tập trắc nghiệm Sinh – Cánh diều Đề thi, kiểm tra Sinh – Kết nối tri thức Đề thi, kiểm tra Sinh – Chân trời sáng tạo Xem thêmMôn Lịch sử Lớp 10SGK Lịch sử – Kết nối tri thức SGK Lịch sử – Chân trời sáng tạo SGK Lịch sử – Cánh Diều SBT Lịch sử – Kết nối tri thức SBT Lịch sử – Chân trời sáng tạo SBT Lịch sử – Cánh Diều Chuyên đề học tập Lịch sử – Kết nối tri thức Đề thi, đề kiểm tra Lịch sử – Kết nối tri thức Đề thi, đề kiểm tra Lịch sử lớp 10 – Chân trời sáng tạo Xem thêmMôn Địa lí Lớp 10SGK Địa lí – Kết nối tri thức SGK Địa lí – Cánh Diều SGK Địa lí – Chân trời sáng tạo SBT Địa lí – Kết nối tri thức SBT Địa lí – Chân trời sáng tạo Đề thi, đề kiểm tra Địa lí – Kết nối tri thức Đề thi, đề kiểm tra Địa lí lớp 10 – Chân trời sáng tạo Đề thi, đề kiểm tra Địa lí – Kết nối tri thứcMôn GDCD Lớp 10SGK Giáo dục kinh tế và pháp luật – KNTT SGK Giáo dục kinh tế và pháp luật – CTST SGK Giáo dục kinh tế và pháp luật – Cánh diềuMôn Tin học Lớp 10SGK Tin học – Kết nối tri thức SGK Tin học – Cánh Diều SBT Tin học – Kết nối tri thứcMôn HĐ trải nghiệm, hướng nghiệp Lớp 10SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh DiềuMôn Giáo dục thể chất Lớp 10SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diềuMôn GD Quốc phòng và An ninh Lớp 10SGK Giáo dục quốc phòng và an ninh – Kết nối tri thức SGK Giáo dục quốc phòng và an ninh – Cánh diều HỌC NGAY
Môn Toán học Lớp 9SGK Toán lớp 9 SBT Toán lớp 9 Vở bài tập Toán 9 Bài tập trắc nghiệm Toán 9 Tài liệu Dạy – học Toán 9 Đề thi, đề kiểm tra Toán lớp 9 Đề thi vào 10 môn Toán SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo Xem thêmMôn Ngữ văn Lớp 9Soạn văn 9 siêu ngắn Soạn văn 9 chi tiết Tác giả – Tác phẩm văn 9 Văn mẫu lớp 9 Vở bài tập Ngữ văn lớp 9 Bài tập trắc nghiệm Văn 9 Đề thi vào 10 môn Văn Đề thi, đề kiểm tra Văn 9 Soạn văn – Kết nối tri thức Xem thêmMôn Tiếng Anh Lớp 9Tiếng Anh – Friends Plus Tiếng Anh – iLearn Smart World Tiếng Anh – Right on! Tiếng Anh – English Discovery SGK Tiếng Anh lớp 9 Mới SGK Tiếng Anh lớp 9 SBT Tiếng Anh lớp 9 mới Vở bài tập Tiếng Anh 9 Bài tập trắc nghiệm Tiếng Anh 9 mới Xem thêmMôn Vật lí Lớp 9SGK Vật lí lớp 9 SBT Vật lí lớp 9 Vở bài tập Vật lí 9 Bài tập trắc nghiệm Lí 9 Tài liệu Dạy – Học Vật lí 9 Đề thi, kiểm tra Lí lớp 9Môn Hóa học Lớp 9SGK Hóa lớp 9 SBT Hóa lớp 9 Vở bài tập Hoá học 9 Bài tập trắc nghiệm Hóa 9 Tài liệu Dạy – học Hóa học 9 Đề thi, đề kiểm tra Hóa lớp 9Môn Sinh học Lớp 9SGK Sinh lớp 9 SBT Sinh lớp 9 Vở bài tập Sinh học 9 Đề thi, đề kiểm tra Sinh lớp 9 Bài tập trắc nghiệm Sinh 9 Đề thi, đề kiểm tra Sinh lớp 9Môn Lịch sử Lớp 9SGK Lịch sử lớp 9 VBT Lịch sử lớp 9 Tập bản đồ Lịch sử lớp 9 SBT Lịch sử lớp 9 Đề thi, kiểm tra Lịch sử lớp 9Môn Địa lí Lớp 9Đề thi, kiểm tra Địa lí lớp 9 SGK Địa lí lớp 9 SBT Địa lí lớp 9 VBT Địa lí lớp 9 Tập bản đồ Địa lí lớp 9Môn Công nghệ Lớp 9SGK Công nghệ 9Môn Tin học Lớp 9SGK Tin học lớp 9Môn Khoa học tự nhiên Lớp 9SGK Khoa học tự nhiên – Cánh diều SGK Khoa học tự nhiên – Chân trời sáng tạo SGK Khoa học tự nhiên – Kết nối tri thứcMôn Âm nhạc và mỹ thuật Lớp 9Âm nhạc và mỹ thuật lớp 9
HỌC NGAY
Môn Toán học Lớp 9SGK Toán lớp 9 SBT Toán lớp 9 Vở bài tập Toán 9 Bài tập trắc nghiệm Toán 9 Tài liệu Dạy – học Toán 9 Đề thi, đề kiểm tra Toán lớp 9 Đề thi vào 10 môn Toán SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo Xem thêmMôn Ngữ văn Lớp 9Soạn văn 9 siêu ngắn Soạn văn 9 chi tiết Tác giả – Tác phẩm văn 9 Văn mẫu lớp 9 Vở bài tập Ngữ văn lớp 9 Bài tập trắc nghiệm Văn 9 Đề thi vào 10 môn Văn Đề thi, đề kiểm tra Văn 9 Soạn văn – Kết nối tri thức Xem thêmMôn Tiếng Anh Lớp 9Tiếng Anh – Friends Plus Tiếng Anh – iLearn Smart World Tiếng Anh – Right on! Tiếng Anh – English Discovery SGK Tiếng Anh lớp 9 Mới SGK Tiếng Anh lớp 9 SBT Tiếng Anh lớp 9 mới Vở bài tập Tiếng Anh 9 Bài tập trắc nghiệm Tiếng Anh 9 mới Xem thêmMôn Vật lí Lớp 9SGK Vật lí lớp 9 SBT Vật lí lớp 9 Vở bài tập Vật lí 9 Bài tập trắc nghiệm Lí 9 Tài liệu Dạy – Học Vật lí 9 Đề thi, kiểm tra Lí lớp 9Môn Hóa học Lớp 9SGK Hóa lớp 9 SBT Hóa lớp 9 Vở bài tập Hoá học 9 Bài tập trắc nghiệm Hóa 9 Tài liệu Dạy – học Hóa học 9 Đề thi, đề kiểm tra Hóa lớp 9Môn Sinh học Lớp 9SGK Sinh lớp 9 SBT Sinh lớp 9 Vở bài tập Sinh học 9 Đề thi, đề kiểm tra Sinh lớp 9 Bài tập trắc nghiệm Sinh 9 Đề thi, đề kiểm tra Sinh lớp 9Môn Lịch sử Lớp 9SGK Lịch sử lớp 9 VBT Lịch sử lớp 9 Tập bản đồ Lịch sử lớp 9 SBT Lịch sử lớp 9 Đề thi, kiểm tra Lịch sử lớp 9Môn Địa lí Lớp 9Đề thi, kiểm tra Địa lí lớp 9 SGK Địa lí lớp 9 SBT Địa lí lớp 9 VBT Địa lí lớp 9 Tập bản đồ Địa lí lớp 9Môn Công nghệ Lớp 9SGK Công nghệ 9Môn Tin học Lớp 9SGK Tin học lớp 9Môn Khoa học tự nhiên Lớp 9SGK Khoa học tự nhiên – Cánh diều SGK Khoa học tự nhiên – Chân trời sáng tạo SGK Khoa học tự nhiên – Kết nối tri thứcMôn Âm nhạc và mỹ thuật Lớp 9Âm nhạc và mỹ thuật lớp 9 HỌC NGAY
Môn Toán học Lớp 8SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SGK Toán 8 – Cùng khám phá SBT Toán – Kết nối tri thức SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Vở thực hành Toán Đề thi, đề kiểm tra Toán – Kết nối tri thức Xem thêmMôn Ngữ văn Lớp 8Soạn văn chi tiết – KNTT Văn mẫu – Chân trời sáng tạo Soạn văn siêu ngắn – KNTT Văn mẫu – Cánh Diều Soạn văn chi tiết – CTST Đề thi, đề kiểm tra Văn – Kết nối tri thức Soạn văn siêu ngắn – CTST Đề thi, đề kiểm tra Văn – Cánh diều Soạn văn chi tiết – Cánh diều Xem thêmMôn Tiếng Anh Lớp 8Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Đề thi, đề kiểm tra Tiếng Anh 8 mới Lý thuyết Tiếng Anh 8 Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Tiếng Anh – Global Success Tiếng Anh – Friends Plus Tiếng Anh – iLearn Smart World Xem thêmMôn GDCD Lớp 8Giáo dục công dân – Kết nối tri thức Giáo dục công dân – Chân trời sáng tạo Giáo dục công dân – Cánh diềuMôn Công nghệ Lớp 8SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 8SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 8SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diều SGK Giáo dục thể chất – Chân trời sáng tạoMôn Khoa học tự nhiên Lớp 8SGK Khoa học tự nhiên – Kết nối tri thức SGK Khoa học tự nhiên – Cánh diều SBT KHTN – Kết nối tri thức SBT KHTN – Cánh diều Vở thực hành Khoa học tự nhiên Đề thi, đề kiểm tra KHTN – Kết nối tri thức Đề thi, đề kiểm tra KHTN – Cánh diều Lý thuyết Khoa học tự nhiên 8 Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Xem thêmMôn Lịch sử và Địa lí Lớp 8SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Cánh diều SGK Lịch sử và Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Lịch Sử và Địa lí – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Lịch Sử và Địa lí – Cánh diều
HỌC NGAY
Môn Toán học Lớp 8SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SGK Toán 8 – Cùng khám phá SBT Toán – Kết nối tri thức SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Vở thực hành Toán Đề thi, đề kiểm tra Toán – Kết nối tri thức Xem thêmMôn Ngữ văn Lớp 8Soạn văn chi tiết – KNTT Văn mẫu – Chân trời sáng tạo Soạn văn siêu ngắn – KNTT Văn mẫu – Cánh Diều Soạn văn chi tiết – CTST Đề thi, đề kiểm tra Văn – Kết nối tri thức Soạn văn siêu ngắn – CTST Đề thi, đề kiểm tra Văn – Cánh diều Soạn văn chi tiết – Cánh diều Xem thêmMôn Tiếng Anh Lớp 8Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Đề thi, đề kiểm tra Tiếng Anh 8 mới Lý thuyết Tiếng Anh 8 Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Tiếng Anh – Global Success Tiếng Anh – Friends Plus Tiếng Anh – iLearn Smart World Xem thêmMôn GDCD Lớp 8Giáo dục công dân – Kết nối tri thức Giáo dục công dân – Chân trời sáng tạo Giáo dục công dân – Cánh diềuMôn Công nghệ Lớp 8SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 8SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 8SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diều SGK Giáo dục thể chất – Chân trời sáng tạoMôn Khoa học tự nhiên Lớp 8SGK Khoa học tự nhiên – Kết nối tri thức SGK Khoa học tự nhiên – Cánh diều SBT KHTN – Kết nối tri thức SBT KHTN – Cánh diều Vở thực hành Khoa học tự nhiên Đề thi, đề kiểm tra KHTN – Kết nối tri thức Đề thi, đề kiểm tra KHTN – Cánh diều Lý thuyết Khoa học tự nhiên 8 Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Xem thêmMôn Lịch sử và Địa lí Lớp 8SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Cánh diều SGK Lịch sử và Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Lịch Sử và Địa lí – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Lịch Sử và Địa lí – Cánh diều HỌC NGAY
Môn Toán học Lớp 7SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SBT Toán – Kết nối tri thức SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Xem thêmMôn Ngữ văn Lớp 7Bài tập trắc nghiệm Văn – Kết nối tri thức Bài tập trắc nghiệm Văn – Chân trời sáng tạo Bài tập trắc nghiệm Văn – Cánh diều Vở thực hành văn Lý thuyết Văn 7 SBT Văn – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Kết nối tri thức Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Cánh diều Xem thêmMôn Tiếng Anh Lớp 7Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Lý thuyết Tiếng Anh 7 Bài tập trắc nghiệm Tiếng Anh – Friends Plus Bài tập trắc nghiệm Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Tiếng Anh – Global Success Xem thêmMôn Công nghệ Lớp 7SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn Tin học Lớp 7SGK Tin học – Kết nối tri thức SGK Tin học – Cánh Diều SGK Tin học – Chân trời sáng tạo SBT Tin học – Kết nối tri thứcMôn HĐ trải nghiệm, hướng nghiệp Lớp 7SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh Diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạoMôn Khoa học tự nhiên Lớp 7SGK Khoa học tự nhiên – Kết nối tri thức SGK Khoa học tự nhiên – Chân trời sáng tạo SGK Khoa học tự nhiên – Cánh diều SBT KHTN – Kết nối tri thức SBT KHTN – Chân trời sáng tạo SBT KHTN – Cánh diều Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Bài tập trắc nghiệm Khoa học tự nhiên – Chân trời sáng tạo Bài tập trắc nghiệm Khoa học tự nhiên – Cánh diều Xem thêmMôn Lịch sử và Địa lí Lớp 7SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Chân trời sáng tạo SGK Lịch sử và Địa lí – Cánh Diều SBT Lịch sử và Địa lí – Kết nối tri thức SBT Lịch sử và Địa lí – Chân trời sáng tạo SBT Lịch sử và Địa lí – Cánh diều Đề thi, kiểm tra Lịch sử và Địa lí lớp 7 – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí lớp 7 – Chân trời sáng tạo
HỌC NGAY
Môn Toán học Lớp 7SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SBT Toán – Kết nối tri thức SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Xem thêmMôn Ngữ văn Lớp 7Bài tập trắc nghiệm Văn – Kết nối tri thức Bài tập trắc nghiệm Văn – Chân trời sáng tạo Bài tập trắc nghiệm Văn – Cánh diều Vở thực hành văn Lý thuyết Văn 7 SBT Văn – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Kết nối tri thức Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Cánh diều Xem thêmMôn Tiếng Anh Lớp 7Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Lý thuyết Tiếng Anh 7 Bài tập trắc nghiệm Tiếng Anh – Friends Plus Bài tập trắc nghiệm Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Tiếng Anh – Global Success Xem thêmMôn Công nghệ Lớp 7SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn Tin học Lớp 7SGK Tin học – Kết nối tri thức SGK Tin học – Cánh Diều SGK Tin học – Chân trời sáng tạo SBT Tin học – Kết nối tri thứcMôn HĐ trải nghiệm, hướng nghiệp Lớp 7SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh Diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạoMôn Khoa học tự nhiên Lớp 7SGK Khoa học tự nhiên – Kết nối tri thức SGK Khoa học tự nhiên – Chân trời sáng tạo SGK Khoa học tự nhiên – Cánh diều SBT KHTN – Kết nối tri thức SBT KHTN – Chân trời sáng tạo SBT KHTN – Cánh diều Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Bài tập trắc nghiệm Khoa học tự nhiên – Chân trời sáng tạo Bài tập trắc nghiệm Khoa học tự nhiên – Cánh diều Xem thêmMôn Lịch sử và Địa lí Lớp 7SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Chân trời sáng tạo SGK Lịch sử và Địa lí – Cánh Diều SBT Lịch sử và Địa lí – Kết nối tri thức SBT Lịch sử và Địa lí – Chân trời sáng tạo SBT Lịch sử và Địa lí – Cánh diều Đề thi, kiểm tra Lịch sử và Địa lí lớp 7 – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí lớp 7 – Chân trời sáng tạo HỌC NGAY
Môn Toán học Lớp 6SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SBT Toán – Kết nối tri thức SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Xem thêmMôn Ngữ văn Lớp 6Vở thực hành văn Ôn tập hè Văn lớp 6 Soạn văn siêu ngắn – KNTT Văn mẫu 6- Kết nối tri thức Soạn văn chi tiết – KNTT Văn mẫu 6 – Cánh diều Soạn văn siêu ngắn – CTST Văn mẫu 6 – Chân trời sáng tạo Soạn văn chi tiết – CTST Xem thêmMôn Tiếng Anh Lớp 6Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Ôn tập hè Tiếng Anh lớp 6 Bài tập trắc nghiệm Tiếng Anh 6 – English Discovery Global Success (Pearson) Tiếng Anh – Friends plus Xem thêmMôn GDCD Lớp 6SGK GDCD – CTST SGK GDCD – Cánh Diều SBT GDCD – Kết nối tri thức SBT GDCD – Chân trời sáng tạo SBT GDCD – Cánh diều SGK GDCD – KNTTMôn Công nghệ Lớp 6Công nghệ – Kết nối tri thức Công nghệ – Cánh Diều Công nghệ – Chân trời sáng tạo SBT Công nghệ – Kết nối tri thức SBT Công nghệ – Cánh diều SBT Công nghệ – Chân trời sáng tạoMôn Tin học Lớp 6Tin học – Kết nối tri thức + chân trời sáng tạo Tin học – Cánh Diều SBT Tin học – Kết nối tri thức SBT Tin học – Cánh DiềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 6SGK Trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Trải nghiệm, hướng nghiệp – Chân trời sáng tạo SGK Trải nghiệm, hướng nghiệp – Cánh diều SBT Trải nghiệm, hướng nghiệp – Kết nối tri thức SBT Trải nghiệm, hướng nghiệp – Chân trời sáng tạo Thực hành Trải nghiệm, hướng nghiệp – Cánh diềuMôn Khoa học tự nhiên Lớp 6SGK KHTN – Kết nối tri thức SGK KHTN – Chân trời sáng tạo SGK KHTN – Cánh Diều SBT KHTN – Kết nối tri thức SBT KHTN – Chân trời sáng tạo SBT KHTN – Cánh Diều Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Bài tập trắc nghiệm Khoa học tự nhiên – Chân trời sáng tạo Bài tập trắc nghiệm Khoa học tự nhiên – Cánh diều Xem thêmMôn Lịch sử và Địa lí Lớp 6SGK Lịch sử và Địa lí – KNTT SGK Lịch sử và Địa lí – CTST SGK Lịch sử và Địa lí – Cánh Diều SBT Lịch sử và Địa lí – KNTT SBT Lịch sử và Địa lí – CTST SBT Lịch sử và Địa lí – Cánh diều Đề thi, kiểm tra Lịch sử và Địa lí – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí – Cánh Diều Đề thi, kiểm tra Lịch sử và Địa lí – Chân trời sáng tạoMôn Mỹ thuật Lớp 6Mĩ thuật – Kết nối tri thức Mĩ thuật – Chân trời sáng tạo Mĩ thuật – Cánh diều
HỌC NGAY
Môn Toán học Lớp 6SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SBT Toán – Kết nối tri thức SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Xem thêmMôn Ngữ văn Lớp 6Vở thực hành văn Ôn tập hè Văn lớp 6 Soạn văn siêu ngắn – KNTT Văn mẫu 6- Kết nối tri thức Soạn văn chi tiết – KNTT Văn mẫu 6 – Cánh diều Soạn văn siêu ngắn – CTST Văn mẫu 6 – Chân trời sáng tạo Soạn văn chi tiết – CTST Xem thêmMôn Tiếng Anh Lớp 6Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Ôn tập hè Tiếng Anh lớp 6 Bài tập trắc nghiệm Tiếng Anh 6 – English Discovery Global Success (Pearson) Tiếng Anh – Friends plus Xem thêmMôn GDCD Lớp 6SGK GDCD – CTST SGK GDCD – Cánh Diều SBT GDCD – Kết nối tri thức SBT GDCD – Chân trời sáng tạo SBT GDCD – Cánh diều SGK GDCD – KNTTMôn Công nghệ Lớp 6Công nghệ – Kết nối tri thức Công nghệ – Cánh Diều Công nghệ – Chân trời sáng tạo SBT Công nghệ – Kết nối tri thức SBT Công nghệ – Cánh diều SBT Công nghệ – Chân trời sáng tạoMôn Tin học Lớp 6Tin học – Kết nối tri thức + chân trời sáng tạo Tin học – Cánh Diều SBT Tin học – Kết nối tri thức SBT Tin học – Cánh DiềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 6SGK Trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Trải nghiệm, hướng nghiệp – Chân trời sáng tạo SGK Trải nghiệm, hướng nghiệp – Cánh diều SBT Trải nghiệm, hướng nghiệp – Kết nối tri thức SBT Trải nghiệm, hướng nghiệp – Chân trời sáng tạo Thực hành Trải nghiệm, hướng nghiệp – Cánh diềuMôn Khoa học tự nhiên Lớp 6SGK KHTN – Kết nối tri thức SGK KHTN – Chân trời sáng tạo SGK KHTN – Cánh Diều SBT KHTN – Kết nối tri thức SBT KHTN – Chân trời sáng tạo SBT KHTN – Cánh Diều Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Bài tập trắc nghiệm Khoa học tự nhiên – Chân trời sáng tạo Bài tập trắc nghiệm Khoa học tự nhiên – Cánh diều Xem thêmMôn Lịch sử và Địa lí Lớp 6SGK Lịch sử và Địa lí – KNTT SGK Lịch sử và Địa lí – CTST SGK Lịch sử và Địa lí – Cánh Diều SBT Lịch sử và Địa lí – KNTT SBT Lịch sử và Địa lí – CTST SBT Lịch sử và Địa lí – Cánh diều Đề thi, kiểm tra Lịch sử và Địa lí – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí – Cánh Diều Đề thi, kiểm tra Lịch sử và Địa lí – Chân trời sáng tạoMôn Mỹ thuật Lớp 6Mĩ thuật – Kết nối tri thức Mĩ thuật – Chân trời sáng tạo Mĩ thuật – Cánh diều HỌC NGAY
Môn Toán học Lớp 5SGK Toán lớp 5 VNEN Toán lớp 5 Vở bài tập Toán 5 Bài tập cuối tuần Toán 5 Cùng em học toán lớp 5 Bài tập trắc nghiệm Toán 5 Đề thi, đề kiểm tra Toán lớp 5 Bài tập phát triển năng lực Toán lớp 5 Toán nâng cao lớp 5 Xem thêmMôn Tiếng Anh Lớp 5SGK Tiếng Anh lớp 5 Mới Đề thi vào lớp 6 môn Tiếng Anh Chứng chỉ Cambridge Pre A1 Starters SBT Tiếng Anh lớp 5 Đề thi, đề kiểm tra Tiếng Anh lớp 5 Tiếng Anh – Global Success Tiếng Anh – Family and Friends Tiếng Anh – iLearn Smart Start Tiếng Anh – Explore Our WorldMôn Lịch sử và Địa lí Lớp 5SGK Lịch sử và Địa lí lớp 5 Vở bài tập Lịch sử lớp 5 Vở bài tập Địa lí lớp 5
HỌC NGAY
Môn Toán học Lớp 5SGK Toán lớp 5 VNEN Toán lớp 5 Vở bài tập Toán 5 Bài tập cuối tuần Toán 5 Cùng em học toán lớp 5 Bài tập trắc nghiệm Toán 5 Đề thi, đề kiểm tra Toán lớp 5 Bài tập phát triển năng lực Toán lớp 5 Toán nâng cao lớp 5 Xem thêmMôn Tiếng Anh Lớp 5SGK Tiếng Anh lớp 5 Mới Đề thi vào lớp 6 môn Tiếng Anh Chứng chỉ Cambridge Pre A1 Starters SBT Tiếng Anh lớp 5 Đề thi, đề kiểm tra Tiếng Anh lớp 5 Tiếng Anh – Global Success Tiếng Anh – Family and Friends Tiếng Anh – iLearn Smart Start Tiếng Anh – Explore Our WorldMôn Lịch sử và Địa lí Lớp 5SGK Lịch sử và Địa lí lớp 5 Vở bài tập Lịch sử lớp 5 Vở bài tập Địa lí lớp 5 HỌC NGAY
Môn Toán học Lớp 4SGK Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Cánh diều SGK Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Chân trời sáng tạo SGK Toán – Cánh diều SGK Toán 4 – Bình Minh VBT Toán – Kết nối tri thức Vở thực hành Toán Bài tập phát triển năng lực Toán lớp 4 Xem thêmMôn Tiếng Anh Lớp 4Tiếng Anh – Global Sucess Đề thi, đề kiểm tra Tiếng Anh – Phonics Smart Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh – Explore Our World Tiếng Anh – iLearn Smart Start Chứng chỉ Cambridge Pre A1 Starters Tiếng Anh – Phonics Smart SBT Tiếng Anh lớp 4 Tiếng Anh – Explore Our World Xem thêmMôn Công nghệ Lớp 4SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 4SGK Hoạt động trải nghiệm – Kết nối tri thức SGK Hoạt động trải nghiệm – Cánh diều SGK Hoạt động trải nghiệm – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 4SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diều SGK Giáo dục thể chất – Chân trời sáng tạoMôn Lịch sử và Địa lí Lớp 4SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Chân trời sáng tạo SGK Lịch sử và Địa lí – Cánh diềuMôn Âm nhạc Lớp 4SGK Âm nhạc – Kết nối tri thức SGK Âm nhạc – Chân trời sáng tạo SGK Âm nhạc – Cánh diềuMôn Mỹ thuật Lớp 4SGK Mĩ thuật – Kết nối tri thức SGK Mĩ thuật – Cánh diều SGK Mĩ thuật – Chân trời sáng tạo bản 1 SGK Mĩ thuật – Chân trời sáng tạo bản 2Môn Tiếng việt Lớp 4Đề thi, đề kiểm tra Tiếng Việt – Kết nối tri thức Đề thi, đề kiểm tra Tiếng Việt – Chân trời sáng tạo Đề thi, đề kiểm tra Tiếng Việt – Cánh diều Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh diều VBT Tiếng Việt – Kết nối tri thức SGK Tiếng Việt 4 Cùng em học Tiếng Việt 4 Xem thêm
HỌC NGAY
Môn Toán học Lớp 4SGK Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Cánh diều SGK Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Chân trời sáng tạo SGK Toán – Cánh diều SGK Toán 4 – Bình Minh VBT Toán – Kết nối tri thức Vở thực hành Toán Bài tập phát triển năng lực Toán lớp 4 Xem thêmMôn Tiếng Anh Lớp 4Tiếng Anh – Global Sucess Đề thi, đề kiểm tra Tiếng Anh – Phonics Smart Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh – Explore Our World Tiếng Anh – iLearn Smart Start Chứng chỉ Cambridge Pre A1 Starters Tiếng Anh – Phonics Smart SBT Tiếng Anh lớp 4 Tiếng Anh – Explore Our World Xem thêmMôn Công nghệ Lớp 4SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 4SGK Hoạt động trải nghiệm – Kết nối tri thức SGK Hoạt động trải nghiệm – Cánh diều SGK Hoạt động trải nghiệm – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 4SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diều SGK Giáo dục thể chất – Chân trời sáng tạoMôn Lịch sử và Địa lí Lớp 4SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Chân trời sáng tạo SGK Lịch sử và Địa lí – Cánh diềuMôn Âm nhạc Lớp 4SGK Âm nhạc – Kết nối tri thức SGK Âm nhạc – Chân trời sáng tạo SGK Âm nhạc – Cánh diềuMôn Mỹ thuật Lớp 4SGK Mĩ thuật – Kết nối tri thức SGK Mĩ thuật – Cánh diều SGK Mĩ thuật – Chân trời sáng tạo bản 1 SGK Mĩ thuật – Chân trời sáng tạo bản 2Môn Tiếng việt Lớp 4Đề thi, đề kiểm tra Tiếng Việt – Kết nối tri thức Đề thi, đề kiểm tra Tiếng Việt – Chân trời sáng tạo Đề thi, đề kiểm tra Tiếng Việt – Cánh diều Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh diều VBT Tiếng Việt – Kết nối tri thức SGK Tiếng Việt 4 Cùng em học Tiếng Việt 4 Xem thêm HỌC NGAY
Môn Toán học Lớp 3Đề thi, đề kiểm tra Toán – Kết nối tri thức Bài tập cuối tuần môn Toán 3 Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Cùng em học Toán 3 Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Ôn tập hè Toán – Kết nối tri thức Xem thêmMôn Tiếng Anh Lớp 3Đề thi, đề kiểm tra Tiếng Anh – Phonics Smart Chứng chỉ Cambridge Pre A1 Starters Bài tập trắc nghiệm Tiếng Anh – iLearn Smart Start Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh – Explore Our World Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart Start Tiếng Anh – Global Success Tiếng Anh – Family and Friends Xem thêmMôn Tin học Lớp 3SGK Tin học – Kết nối tri thức SGK Tin học – Chân trời sáng tạo SGK Tin học – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 3SGK Hoạt động trải nghiệm- Kết nối tri thức SGK Hoạt động trải nghiệm- Chân trời sáng tạo SGK Hoạt động trải nghiệm – Cánh diềuMôn Tiếng việt Lớp 3Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh diều VBT Tiếng Việt – Kết nối tri thức VBT Tiếng Việt – Chân trời sáng tạo VBT Tiếng Việt – Cánh diều Văn mẫu – Kết nối tri thức Cùng em học Tiếng Việt 3 Văn mẫu lớp 3Môn Tự nhiên và xã hội Lớp 3Tự nhiên và xã hội – Kết nối tri thức Tự nhiên và xã hội – Chân trời sáng tạo Tự nhiên và xã hội – Cánh diều
HỌC NGAY
Môn Toán học Lớp 3Đề thi, đề kiểm tra Toán – Kết nối tri thức Bài tập cuối tuần môn Toán 3 Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Cùng em học Toán 3 Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Ôn tập hè Toán – Kết nối tri thức Xem thêmMôn Tiếng Anh Lớp 3Đề thi, đề kiểm tra Tiếng Anh – Phonics Smart Chứng chỉ Cambridge Pre A1 Starters Bài tập trắc nghiệm Tiếng Anh – iLearn Smart Start Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh – Explore Our World Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart Start Tiếng Anh – Global Success Tiếng Anh – Family and Friends Xem thêmMôn Tin học Lớp 3SGK Tin học – Kết nối tri thức SGK Tin học – Chân trời sáng tạo SGK Tin học – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 3SGK Hoạt động trải nghiệm- Kết nối tri thức SGK Hoạt động trải nghiệm- Chân trời sáng tạo SGK Hoạt động trải nghiệm – Cánh diềuMôn Tiếng việt Lớp 3Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh diều VBT Tiếng Việt – Kết nối tri thức VBT Tiếng Việt – Chân trời sáng tạo VBT Tiếng Việt – Cánh diều Văn mẫu – Kết nối tri thức Cùng em học Tiếng Việt 3 Văn mẫu lớp 3Môn Tự nhiên và xã hội Lớp 3Tự nhiên và xã hội – Kết nối tri thức Tự nhiên và xã hội – Chân trời sáng tạo Tự nhiên và xã hội – Cánh diều HỌC NGAY
Môn Toán học Lớp 2SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh Diều VBT Toán – KNTT VBT Toán – CTST Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Cùng em học Toán 2 Xem thêmMôn Tiếng Anh Lớp 2Đề thi, đề kiểm tra Tiếng Anh – Phonics Smart Đề thi, đề kiểm tra Tiếng Anh – English Discovery Chứng chỉ Cambridge Pre A1 Starters SBT Kết nối tri thức SBT Family and Friends SBT iLearn Smart Start SBT Phonics Smart SBT English Discovery SBT Explore Our World Xem thêmMôn HĐ trải nghiệm, hướng nghiệp Lớp 2VBT Hoạt động trải nghiệm – Chân trời sáng tạo VTH Hoạt động trải nghiệm – Cánh Diều VBT Hoạt động trải nghiệm – Kết nối tri thứcMôn Âm nhạc Lớp 2Âm nhạc 2 – Kết nối tri thức Âm nhạc 2 – Chân trời sáng tạo Âm nhạc 2 – Cánh diều VBT Âm nhạc – Kết nối tri thức VBT Âm nhạc – Chân trời sáng tạo VBT Âm nhạc – Cánh diềuMôn Tiếng việt Lớp 2Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh Diều Văn mẫu – Kết nối tri thức Văn mẫu – Chân trời sáng tạo Văn mẫu – Cánh diều VBT Tiếng Việt – Kết nối tri thức VBT Tiếng Việt – Chân trời sáng tạo VBT Tiếng Việt – Cánh diều Xem thêm
HỌC NGAY
Môn Toán học Lớp 2SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh Diều VBT Toán – KNTT VBT Toán – CTST Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Cùng em học Toán 2 Xem thêmMôn Tiếng Anh Lớp 2Đề thi, đề kiểm tra Tiếng Anh – Phonics Smart Đề thi, đề kiểm tra Tiếng Anh – English Discovery Chứng chỉ Cambridge Pre A1 Starters SBT Kết nối tri thức SBT Family and Friends SBT iLearn Smart Start SBT Phonics Smart SBT English Discovery SBT Explore Our World Xem thêmMôn HĐ trải nghiệm, hướng nghiệp Lớp 2VBT Hoạt động trải nghiệm – Chân trời sáng tạo VTH Hoạt động trải nghiệm – Cánh Diều VBT Hoạt động trải nghiệm – Kết nối tri thứcMôn Âm nhạc Lớp 2Âm nhạc 2 – Kết nối tri thức Âm nhạc 2 – Chân trời sáng tạo Âm nhạc 2 – Cánh diều VBT Âm nhạc – Kết nối tri thức VBT Âm nhạc – Chân trời sáng tạo VBT Âm nhạc – Cánh diềuMôn Tiếng việt Lớp 2Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh Diều Văn mẫu – Kết nối tri thức Văn mẫu – Chân trời sáng tạo Văn mẫu – Cánh diều VBT Tiếng Việt – Kết nối tri thức VBT Tiếng Việt – Chân trời sáng tạo VBT Tiếng Việt – Cánh diều Xem thêm HỌC NGAY
Môn Tiếng Anh Lớp 1Chứng chỉ Cambridge Pre A1 StartersMôn Tiếng việt Lớp 1Đề thi, đề kiểm tra Tiếng Việt 1 SGK Tiếng Việt – Kết nối tri thức SGK Tiếng Việt – Chân trời sáng tạo SGK Tiếng Việt – Cánh diềuMôn Đạo đức Lớp 1VBT Đạo Đức 1
HỌC NGAY
Môn Tiếng Anh Lớp 1Chứng chỉ Cambridge Pre A1 StartersMôn Tiếng việt Lớp 1Đề thi, đề kiểm tra Tiếng Việt 1 SGK Tiếng Việt – Kết nối tri thức SGK Tiếng Việt – Chân trời sáng tạo SGK Tiếng Việt – Cánh diềuMôn Đạo đức Lớp 1VBT Đạo Đức 1