1. Đề cương ôn tập học kì 1

A. NỘI DUNG ÔN TẬP

Đại số

1. Các phép toán cộng, trừ, nhân, chia đa thức nhiều biến.

– Phép cộng và phép trừ đa thức

– Phép nhân đa thức

– Phép chia đa thức cho đơn thức

2. Hằng đẳng thức đáng nhớ; phân tích đa thức thành nhân tử.

– Các hằng đẳng thức đáng nhớ

\(\begin{array}{l}1.{\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\\2.{\left( {A – B} \right)^2} = {A^2} – 2AB + {B^2}\\3.{A^2} – {B^2} = \left( {A – B} \right)\left( {A + B} \right)\\4.{\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\\5.\left( {A – {B^3}} \right) = {A^3} – 3{A^2}B + 3A{B^2} – {B^3}\\6.{A^3} + {B^3} = \left( {A + B} \right)\left( {{A^2} – AB + {B^2}} \right)\\7.{A^3} – {B^3} = \left( {A – B} \right)\left( {{A^2} + AB + {B^2}} \right)\end{array}\)

– Phân tích đa thức thành nhân tử

Hình học

1. Tứ giác: các định nghĩa, tính chất và dấu hiệu nhận biết.

– Tứ giác

– Hình thang cân

– Hình bình hành

– Hình chữ nhật

– Hình thoi

– Hình vuông

2. Định lí Thales trong tam giác.

– Định lí Thales

– Đường trung bình

– Đường phân giác

Dữ liệu – biểu đồ

– Thu thập và phân tích dữ liệu

– Biểu diễn dữ liệu bằng bảng, biểu đồ

– Phân tích dữ liệu thống kê dựa vào biểu đồ

B. BÀI TẬP

Đề bài

I. Phần trắc nghiệm

Câu 1: Tính giá trị biểu thức \(B = 5{x^2} – 3x – 18\) tại \(\left| x \right| = 3\).

A. \(B = 18\).

B. \(B = 18\) hoặc \(B = 36\).

C. \(B = 36\).

D. \(B = – 18\) hoặc \(B = 36\).

Câu 2: Cho \(A = 4{x^4} + 2{y^2}x – 3{z^3} + 5\) và \(B = – 4{z^3} + 8 + 3{y^2}x – 5{x^4}\). Kết quả của \(A – B\) là:

A. \(9{x^4} + {y^2}x + {z^3} – 3\).

B. \( – {x^4} + 5{y^2}x + {z^3} + 13\).

C. \(9{x^4} – {y^2}x + {z^3} – 3\).

D. \(9{x^4} – {y^2}x + {z^3} + 3\).

Câu 3: Thương \(\left( { – 12{x^4}y + 4{x^3} – 8{x^2}{y^2}} \right):\left( { – 4{x^2}} \right)\) bằng

A. \( – 3{x^2}y + x – 2{y^2}\).

B. \(3{x^4}y + {x^3} – 2{x^2}{y^2}\).

C. \( – 12{x^2}y + 4x – 2{y^2}\).

D. \(3{x^2}y – x + 2{y^2}\).

Câu 4: Kết quả của tích \(\left( {2x + y} \right)\left( {2x – y} \right)\) là:

A. \(4x – y\).

B. \(4x + y\).

C. \(4{x^2} – {y^2}\).

D. \(4{x^2} + {y^2}\).

Câu 5: Kết quả \(8{x^3} + 12{x^2}y + 6x{y^2} + {y^3}\) là:

A. \({\left( {2{x^3} + y} \right)^3}\).

B. \({\left( {2x + {y^3}} \right)^3}\).

C. \({\left( {2x + y} \right)^3}\).

D. \({\left( {2x – y} \right)^3}\).

Câu 6: Điền đơn thức vào chỗ trống: \(\left( {3x + y} \right)\left( {……. – 3xy + {y^2}} \right) = 27{x^3} + {y^3}\)

A. \(9x\).

B. \(6{x^2}\).

C. \(9xy\).

D. \(9{x^2}\).

Câu 7: Đa thức \(12x – 9 – 4{x^2}\) được phân tích thành

A. \(\left( {2x – 3} \right)\left( {2x + 3} \right)\).

B. \( – {\left( {2x – 3} \right)^2}\).

C. \({\left( {3 – 2x} \right)^2}\).

D. \( – {\left( {2x + 3} \right)^2}\).

Câu 8: Cho \(ab\left( {x – 5} \right) – {a^2}\left( {5 – x} \right) = a\left( {x – 5} \right)\left( {…} \right)\). Biểu thức thích hợp điền vào dấu … là

A. 2a + b.

B. 1 + b.

C. a² + ab.

D. a + b.

Câu 9: Hình bình hành là tứ giác có

A. hai cạnh song song.

B. các cạnh đối song song.

C. các góc bằng nhau.

D. các góc đối bù nhau.

Câu 10: Hai đường chéo của hình chữ nhật

A. song song với nhau.

B. bằng nhau.

C. vuông góc với nhau.

D. là các đường phân giác của các góc.

Câu 11: Một tứ giác là hình vuông nếu nó

A. có ba góc vuông.

B. là hình thoi có một góc vuông.

C. là hình bình hành có một góc vuông.

D. là hình thang có hai góc vuông.

Câu 12: Hình thang cân là hình thang

A. có hai cạnh bên bằng nhau.

B. có hai cạnh đáy bằng nhau.

C. có hai góc kề một cạnh bên bù nhau.

D. có hai góc kề một đáy bằng nhau.

Câu 13: Khẳng định nào sau đây là sai?

A. Hình thang cân có một góc vuông là hình chữ nhật.

B. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

C. Hình bình hành có hai đường chéo vuông góc với nhau là hình chữ nhật.

D. Tứ giác có bốn góc bằng nhau là hình chữ nhật.

Câu 14: Cho tam giác ABC có AM là đường trung tuyến, ta có:

A. \({S_{\Delta ABM}} = 2{S_{\Delta ABC}}\).

B. \({S_{\Delta ABM}} = {S_{\Delta ABC}}\).

C. \({S_{\Delta AMC}} = 2{S_{\Delta ABC}}\).

D. \({S_{\Delta ABC}} = 2{S_{\Delta ABM}}\).

Câu 15: Cho tam giác ABC, qua điểm D thuộc cạnh BC, kẻ các đường thẳng song song với AB và AC, cắt AC và AB theo thứ tự tại E và F. Tam giác ABC cần thêm điều kiện gì để AEDF là hình chữ nhật?

A. cân tại A.

B. vuông tại A.

C. \(\widehat B = {60^o}\).

D. \(\widehat B = {30^0}\).

Câu 16: Cho tam giác ABC, D là trung điểm của BC. Qua D kẻ các đường thẳng song song với AB và AC, cắt AC và AB theo thứ tự ở E và F. Tam giác ABC cần thêm điều kiện gì để AEDF là hình vuông?

A. cân tại A.

B. vuông tại A.

C. vuông cân tại A.

D. \(\widehat A = {60^0}\).

Câu 17: Hình bình hành cần thêm điều kiện gì để trở thành hình vuông?

A. Hai đường chéo bằng nhau.

B. Hai đường chéo cắt nhau tại trung điểm mỗi đường.

C. Hai cạnh kề bằng nhau.

D. Có một góc vuông và hai đường chéo vuông góc với nhau.

Câu 18: Cho tam giác ABC có ba đường trung tuyến AI, BD, CE đồng quy tại G. Gọi M và N lần lượt là trung điểm của GC và GB. Khi đó tứ giác MNED là hình gì?

A. Hình chữ nhật.

B. Hình bình hành.

C. Hình thang cân.

D. Hình thang vuông.

Câu 19: Viết tỉ số cặp đoạn thẳng có độ dài như sau: AB = 4dm, CD = 20dm.

A. \(\frac{{AB}}{{CD}} = \frac{1}{4}\).

B. \(\frac{{AB}}{{CD}} = \frac{1}{5}\).

C. \(\frac{{AB}}{{CD}} = \frac{1}{6}\).

D. \(\frac{{AB}}{{CD}} = \frac{1}{7}\).

Câu 20: Cho hình vẽ bên, biết DE // AC, tìm x.

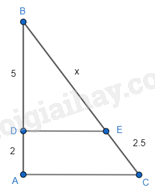
A. x = 6,5.

B. x = 6,25.

C. x = 5.

D. x = 8.

Câu 21: Cho \(\Delta ABC\) có AB = 9 cm; D \( \in \) AB sao cho AD = 6cm. Kẻ DE // BC (E \( \in \) AC); EF // CD (F \( \in \) AB). Tính độ dài AF.

A. 6cm.

B. 5cm.

C. 4cm.

D. 7cm.

Câu 22: Cho hình thang ABCD (AB // CD); BC = 15cm, E \( \in \) AD; \(\frac{{AE}}{{AD}} = \frac{1}{3}\). Qua E kẻ đường thẳng song song với CD cắt BC tại F. Tính độ dài BF.

A. 15cm.

B. 5cm.

C. 10cm.

D. 7cm.

Câu 23: Cho \(\Delta ABC\), AD là tia phân giác trong của góc A. Hãy chọn câu đúng.

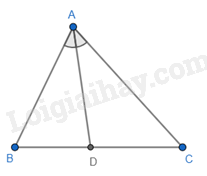
A. \(\frac{{DC}}{{DB}} = \frac{{AB}}{{AC}}\).

B. \(\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}}\).

C. \(\frac{{AB}}{{DB}} = \frac{{DC}}{{AC}}\).

D. \(\frac{{AD}}{{DB}} = \frac{{AC}}{{AD}}\).

Câu 24: Cho \(\Delta ABC\), AD là tia phân giác trong của góc A. Hãy chọn câu sai.

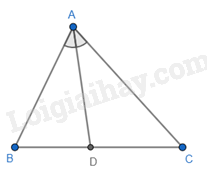
A. \(\frac{{DC}}{{DB}} = \frac{{AC}}{{AB}}\).

B. \(\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}}\).

C. \(\frac{{AB}}{{DB}} = \frac{{DC}}{{AC}}\).

D. \(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\).

Câu 25: Hãy chọn câu đúng. Tính độ dài x, y của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình cùng đơn vị đo là cm.

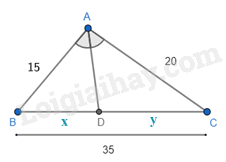
A. x = 12cm; y = 13cm.

B. x = 14cm; y = 11cm.

C. x = 14,3cm; y = 10,7cm.

D. x = 15cm; y = 20cm.

Câu 26: Cho \(\Delta ABC\), AC = 2AB, AD là tia phân giác của tam giác ABC, khi đó \(\frac{{BD}}{{CD}} = ?\)

A. \(\frac{{BD}}{{CD}} = 1\).

B. \(\frac{{BD}}{{CD}} = \frac{1}{3}\).

C. \(\frac{{BD}}{{CD}} = \frac{1}{4}\).

D. \(\frac{{BD}}{{CD}} = \frac{1}{2}\).

Câu 27: Cho \(\Delta ABC\) có chu vi 80cm. Gọi D, E, F là trung điểm của các cạnh AB, AC, BC. Chu vi của \(\Delta DEF\) là:

A. 40cm.

B. 160cm.

C. 80cm.

D. 20cm.

Câu 28: Cho \(\Delta ABC\) có D, E lần lượt là trung điểm của AB, AC và DE = 4cm. Biết đường cao AH = 6cm. Diện tích tam giác ABC là

A. \(S = 24c{m^2}\).

B. \(S = 48c{m^2}\).

C. \(S = 12c{m^2}\).

D. \(S = 32c{m^2}\).

Câu 29: Cho \(\Delta ABC\), các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K lần lượt là trung điểm của GB và GC. Tính EI, DK biết AG = 4cm.

A. EI = DK = 3cm.

B. EI = 3cm, DK = 2cm.

C. EI = DK = 2cm.

D. EI = 1cm, DK = 2cm.

Câu 30: Trong các dữ liệu sau dữ liệu nào là dữ liệu định tính?

A. Số huy chương vàng mà các động viên đã đạt được.

B. Danh sách các động viên tham dự Olympic 2021: Nguyễn Văn Hoàng,……

C. Số học sinh nữ của các tổ trong lớp 7A.

D. Năm sinh của các thành viên trong gia đình em.

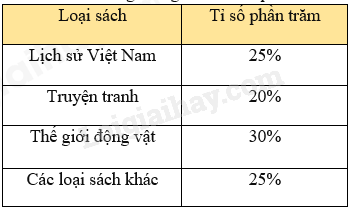
Câu 31: Cho bảng thống kê về tỉ số phần trăm các loại sách trong tủ sách của lớp 8A như sau:

Cho các phát biểu sau:

(I) Dữ liệu định lượng là các loại sách Lịch sử Việt Nam, Truyện tranh, thế giới động vật, các loại sách khác;

(II) Dữ liệu định tính là tỉ số phần trăm: 25%; 20%; 30%; 25%;

(III) Dữ liệu chưa hợp lí là tỉ số phần trăm.

Số phát biểu sai là:

A. 0.

B. 1.

C. 2.

D. 3.

Câu 32: Biểu đồ hình quạt tròn biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022.

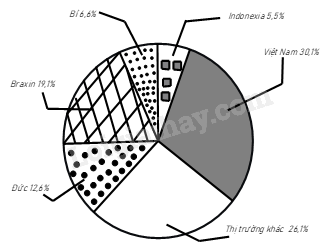
 (Nguồn: Eurostat)

a) Thị trường nào cung cấp cà phê cho Tây Ban Nha là nhiều nhất?

A. Việt Nam.

B. Đức.

C. Braxin.

D. Thị trường khác.

b) Thị trường Việt Nam cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022 gấp khoảng mấy lần thị trường Indonexia?

A. 5,5 lần.

B. 4 lần.

C. 3,2 lần.

D. Kết quả khác.

Câu 33: Biểu đồ cột ở hình vẽ bên biểu diễn tỉ lệ về giá trị đạt được của khoáng sản xuất khẩu nước ngoài của nước ta (tính theo tỉ số phần trăm).

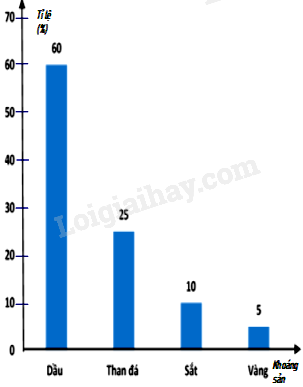
a) Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong biểu đồ cột ở hình bên?

A. Biểu đồ hình quạt tròn.

B. Biểu đồ cột kép.

C. Biểu đồ cột.

D. A; B; C đều đúng.

b) Loại khoáng sản nào có tỉ lệ về giá trị xuất khẩu nước ngoài cao nhất?

A. Dầu.

B. Than đá.

C. Sắt.

D. Vàng.

c) Dựa vào biểu đồ cho biết dữ liệu nào là dữ liệu định tính?

A. Các loại khoáng sản: Dầu, Than đá, Sắt, Vàng.

B. Tỉ lệ về giá trị đạt được của các loại khoáng sản xuất khẩu nước ngoài.

C. A & B đều đúng.

D. A & B đều sai.

Câu 34: Biểu đồ đoạn thẳng dưới đây biểu diễn lượng mưa trung bình các tháng trong năm 2019 tại Thành phố Hồ Chí Minh. Những tháng có lượng mưa trên 300mm là

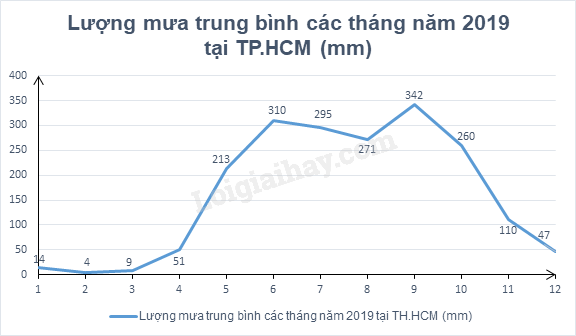
A. tháng 6, 7.

B. tháng 6, 9.

C. tháng 7, 8.

D. tháng 9, 10.

Câu 35: Biểu đồ cột kép dưới đây biểu diễn diện tích gieo trồng sắn của Bình Thuận và Bình Phước trong các năm 2018; 2019; 2020 (đơn vị: Nghìn ha).

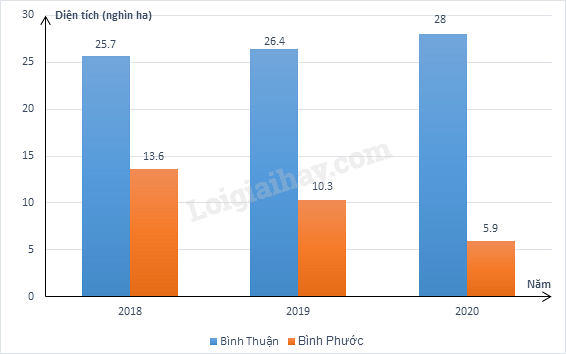
(Nguồn: Niên giám thống kê 2021, NXB Thống kê, 2021)

Diện tích nghìn hecta gieo trồng sắn của Bình Thuận trong năm 2019 là

A. 25,7.

B. 26,4.

C. 10,3.

D. 28.

II. Phần tự luận

Bài 1. Thực hiện các phép tính:

a) \(\left( {x + 3} \right)\left( {x – 3} \right)\).

b) \(\frac{1}{2}x{y^2}.\left( {6xy + \frac{3}{2}{x^3}y – 1} \right)\).

c) \(\left( {2x – y} \right)\left( {4{x^2} + 2xy + {y^2}} \right)\).

d) \(\left( {6{x^5}{y^2} – 9{x^4}{y^3} + 15{x^3}{y^4}} \right):3{x^3}{y^2}\).

Bài 2. Rút gọn các biểu thức:

a) \({\left( {x + y} \right)^2} – {\left( {x – y} \right)^2}\)

b) \({\left( {a + b} \right)^3} + {\left( {a – b} \right)^3} – 2{a^3}\)

c) \(\left( {x + 3} \right)\left( {x + 7} \right) – \left( {x + 1} \right)\left( {x – 1} \right)\)

d) \(\left( {x + 1} \right)\left( {{x^2} – x + 1} \right) – \left( {x – 1} \right)\left( {{x^2} + x + 1} \right)\)

e) \(\left( {2 + 1} \right)\left( {{2^2} + 1} \right)\left( {{2^4} + 1} \right)\left( {{2^8} + 1} \right)\left( {{2^{16}} + 1} \right)\)

Bài 3. Phân tích các đa thức sau thành nhân tử:

a) \(3{x^3} + 6{x^2} + 3x\)

b) \({x^2} – {y^2} – 2x + 2y\)

c) \({x^2} – 25 + {y^2} + 2xy\)

d) \({x^2}\left( {x – 1} \right) + 16\left( {1 – x} \right)\)

e) \(8a\left( {b – c} \right) + 6b\left( {c – b} \right)\)

f) \({x^2} + 8x + 15\)

g) \({x^2} – x – 12\)

h) \({\left( {{x^2} + x} \right)^2} + 3\left( {{x^2} + x} \right) + 2\)

Bài 4. Tìm x, biết:

a) \(2x\left( {x – 5} \right) – x\left( {3 + 2x} \right) = 26\)

b) \(\left( {4x – 1} \right)\left( {x + 3} \right) – {\left( {2x – 1} \right)^2} = 0\)

c) \(5x\left( {x – 1} \right) = x – 1\)

d) \(2\left( {x + 5} \right) – {x^2} – 5x = 0\)

e) \({\left( {2x – 3} \right)^2} – {\left( {x + 5} \right)^2} = 0\)

f) \(3{x^3} – 48x = 0\)

g) \({x^2} – 6x = – 9\)

h) \({x^2} – x – 6 = 0\)

Bài 5. Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến.

a) \(A = 2xy + \frac{1}{2}x.\left( {2x – 4y + 4} \right) – x\left( {x + 2} \right)\)

b) \(B = {\left( {x + 2} \right)^2} – {\left( {x – 3} \right)^2} – 10x\)

Bài 6. Thống kê trong lần kiểm tra cuối học kì I của lớp 8A vừa qua là:

a) Tính tổng số bài kiểm tra cuối học kì I của lớp 8A.

b) Số bài được điểm 10 chiếm bao nhiêu phần trăm so với tổng số bài kiểm tra cuối học kì I của lớp 8A?

Bài 7. Cho biểu đồ về lượng mưa và nhiệt độ trong năm 2022 của Hà Nội

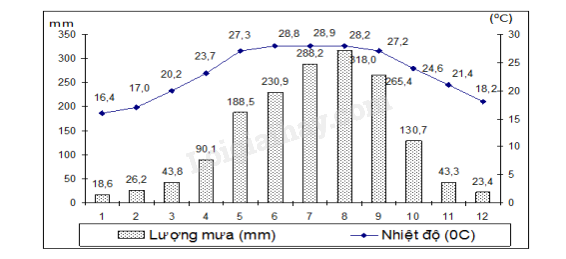
a) Tháng nào có nhiệt độ cao nhất, thấp nhất? Vì sao lại có sự khác biệt này?

b) Tháng nào có lượng mưa nhiều nhất, ít nhất?

c) Em thích tháng nào nhất trong năm và tháng đó có nhiệt độ và lượng mưa như thế nào?

Bài 8. Biểu đồ hình quạt tròn ở hình bên biểu diễn tỉ lệ các yếu tố ảnh hưởng đến sinh trưởng của cây trồng như: Phân bón; Nước tưới; Giống; Kiểm soát dịch hại; Kiểm soát cỏ dại; Yếu tố khác.

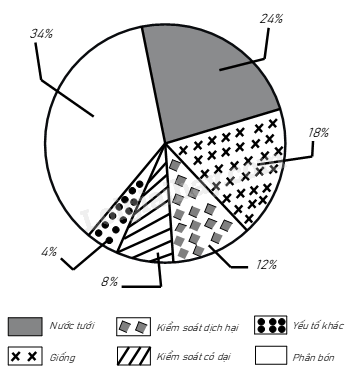
a) Cho biết yếu tố nào ảnh hưởng đến sinh trưởng của cây trồng nhiều nhất?

b) Trong các yếu tố ảnh hưởng đến sinh trưởng của cây thì yếu tố kiểm soát dịch hại gấp mấy lần yếu tố khác?

Bài 9. Cho hình thang ABCD (AB // CD), M là trung điểm của CD. Gọi E là giao điểm của AC và BM, F là giao điểm của BD và AM. Đường thẳng EF cắt BC và AD lần lượt tại G và H.

a) Chứng minh rằng \(\frac{{EA}}{{EC}} = \frac{{2AB}}{{CD}}\).

b) Chứng minh rằng EF // CD.

c) Chứng minh rằng GE = EF = FH.

Bài 10. Cho hình bình hành ABCD, M là trung điểm của AB. Gọi G là giao điểm của AC và DM. Lấy điểm E thuộc đoạn thẳng AM. Các đường thẳng GE và CD cắt nhau tại F.

a) Chứng minh rằng G là trọng tâm của tam giác ABD.

b) Chứng minh rằng GC = 2GA.

c) Kẻ đường thẳng qua G cắt các cạnh AD và BC lần lượt tại I và K. Chứng minh rằng EI // KF.

d) Gọi N là trung điểm của AD. Chứng minh rằng BF = 2EN.

Bài 11. Cho hình vuông ABCD có tâm O, gọi E là trung điểm của AB, DE cắt AC tại F, BF cắt CD tại I.

a) Chứng minh D là trung điểm của IC.

b) Chứng minh ABDI là hình bình hành.

c) Gọi H là trung điểm của AI, CH cắt BD tại L. Chứng minh L là trung điểm của OD.

Bài 12. Để làm cây thông noel, người thợ sẽ dùng một cái khung sắt hình tam giác cân như hình vẽ bên, sau đó gắn mô hình cây thông lên. Cho biết thanh BC = 120cm. Tính độ dài các thanh GF; HE; ID.

Bài 13*. Tính GTNN của biểu thức \(B = {x^2} + 2{y^2} + 3{z^2} – 2xy + 2xz – 2x – 2y – 8z + 2000\).

Bài 14*. Cho a + b = 1. Tính giá trị của biểu thức sau:

\(M = {a^3} + {b^3} + 3ab\left( {{a^2} + {b^2}} \right) + 6{a^2}{b^2}\left( {a + b} \right)\).

——– Hết ——–

Lời giải chi tiết

I. Trắc nghiệm

II. Phần tự luận

Bài 1. Thực hiện các phép tính:

a) \(\left( {x + 3} \right)\left( {x – 3} \right)\).

b) \(\frac{1}{2}x{y^2}.\left( {6xy + \frac{3}{2}{x^3}y – 1} \right)\).

c) \(\left( {2x – y} \right)\left( {4{x^2} + 2xy + {y^2}} \right)\).

d) \(\left( {6{x^5}{y^2} – 9{x^4}{y^3} + 15{x^3}{y^4}} \right):3{x^3}{y^2}\).

Phương pháp

Sử dụng các phép tính với đa thức và các hằng đẳng thức đáng nhớ.

Lời giải

a) \(\left( {x + 3} \right)\left( {x – 3} \right) = {x^2} – {3^2} = {x^2} – 9\)

b) \(\frac{1}{2}x{y^2}.\left( {6xy + \frac{3}{2}{x^3}y – 1} \right)\)

\(\begin{array}{l} = \frac{1}{2}x{y^2}.6xy + \frac{1}{2}x{y^2}.\frac{3}{2}{x^3}y – \frac{1}{2}x{y^2}\\ = 3{x^2}{y^3} + \frac{3}{4}{x^4}.{y^3} – \frac{1}{2}x{y^2}\end{array}\)

c) \(\left( {2x – y} \right)\left( {4{x^2} + 2xy + {y^2}} \right) = {\left( {2x} \right)^3} – {y^3} = 8{x^3} – {y^3}\)

d) \(\left( {6{x^5}{y^2} – 9{x^4}{y^3} + 15{x^3}{y^4}} \right):3{x^3}{y^2}\)

\(\begin{array}{l} = 6{x^5}{y^2}:3{x^3}{y^2} – 9{x^4}{y^3}:3{x^3}{y^2} + 15{x^3}{y^4}:3{x^3}{y^2}\\ = 2{x^2} – 3xy + 5{y^3}\end{array}\)

Bài 2. Rút gọn các biểu thức:

a) \({\left( {x + y} \right)^2} – {\left( {x – y} \right)^2}\)

b) \({\left( {a + b} \right)^3} + {\left( {a – b} \right)^3} – 2{a^3}\)

c) \(\left( {x + 3} \right)\left( {x + 7} \right) – \left( {x + 1} \right)\left( {x – 1} \right)\)

d) \(\left( {x + 1} \right)\left( {{x^2} – x + 1} \right) – \left( {x – 1} \right)\left( {{x^2} + x + 1} \right)\)

e) \(\left( {2 + 1} \right)\left( {{2^2} + 1} \right)\left( {{2^4} + 1} \right)\left( {{2^8} + 1} \right)\left( {{2^{16}} + 1} \right)\)

Phương pháp

Sử dụng các phép tính với đa thức và các hằng đẳng thức đáng nhớ.

Lời giải

a) \({\left( {x + y} \right)^2} – {\left( {x – y} \right)^2}\)\( = \left( {x + y – x + y} \right)\left( {x + y + x – y} \right)\)\( = 2y.2x = 4xy\)

b) \({\left( {a + b} \right)^3} + {\left( {a – b} \right)^3} – 2{a^3}\)\( = {\left( {a + b} \right)^3} – {a^3} + {\left( {a – b} \right)^3} – {a^3}\) \(\begin{array}{l} = \left( {a + b – a} \right)\left[ {{{\left( {a + b} \right)}^2} + a\left( {a + b} \right) + {a^2}} \right] + \left( {a – b – a} \right)\left[ {{{\left( {a – b} \right)}^2} + a\left( {a – b} \right) + {a^2}} \right]\\ = b\left( {{a^2} + 2ab + {b^2} + {a^2} + ab + {a^2}} \right) + \left( { – b} \right)\left( {{a^2} – 2ab + {b^2} + {a^2} – ab + {a^2}} \right)\\ = b\left( {3{a^2} + 3ab + {b^2}} \right) – b\left( {3{a^2} – 3ab + {b^2}} \right)\\ = 3{a^2}b + 3a{b^2} + {b^3} – 3{a^2}b + 3a{b^2} – {b^3}\\ = 6a{b^2}\end{array}\)

c) \(\left( {x + 3} \right)\left( {x + 7} \right) – \left( {x + 1} \right)\left( {x – 1} \right)\)\( = {x^2} + 3x + 7x + 21 – \left( {{x^2} – 1} \right)\)\( = {x^2} + 10x + 21 – {x^2} + 1\)\( = 10x + 22\)

d) \(\left( {x + 1} \right)\left( {{x^2} – x + 1} \right) – \left( {x – 1} \right)\left( {{x^2} + x + 1} \right)\)\( = {x^3} + 1 – \left( {{x^3} – 1} \right)\)\( = {x^3} + 1 – {x^3} + 1\)\( = 2\)

e) \(\left( {2 + 1} \right)\left( {{2^2} + 1} \right)\left( {{2^4} + 1} \right)\left( {{2^8} + 1} \right)\left( {{2^{16}} + 1} \right)\)\( = \frac{{\left( {2 – 1} \right)\left( {2 + 1} \right)\left( {{2^2} + 1} \right)\left( {{2^4} + 1} \right)\left( {{2^8} + 1} \right)\left( {{2^{16}} + 1} \right)}}{{2 – 1}}\)\( = \frac{{\left( {{2^2} – 1} \right)\left( {{2^2} + 1} \right)\left( {{2^4} + 1} \right)\left( {{2^8} + 1} \right)\left( {{2^{16}} + 1} \right)}}{{2 – 1}}\)\( = \frac{{\left( {{2^4} – 1} \right)\left( {{2^4} + 1} \right)\left( {{2^8} + 1} \right)\left( {{2^{16}} + 1} \right)}}{{2 – 1}}\)\( = \frac{{\left( {{2^8} – 1} \right)\left( {{2^8} + 1} \right)\left( {{2^{16}} + 1} \right)}}{{2 – 1}}\)\( = \frac{{\left( {{2^{16}} – 1} \right)\left( {{2^{16}} + 1} \right)}}{{2 – 1}}\)\( = \frac{{{2^{32}} – 1}}{{2 – 1}}\)\( = {2^{32}} – 1\)

Bài 3. Phân tích các đa thức sau thành nhân tử:

a) \(3{x^3} + 6{x^2} + 3x\)

b) \({x^2} – {y^2} – 2x + 2y\)

c) \({x^2} – 25 + {y^2} + 2xy\)

d) \({x^2}\left( {x – 1} \right) + 16\left( {1 – x} \right)\)

e) \(8a\left( {b – c} \right) + 6b\left( {c – b} \right)\)

f) \({x^2} + 8x + 15\)

g) \({x^2} – x – 12\)

h) \({\left( {{x^2} + x} \right)^2} + 3\left( {{x^2} + x} \right) + 2\)

Phương pháp

Sử dụng các phương pháp phân tích đa thức thành nhân tử để phân tích

Lời giải

a) \(3{x^3} + 6{x^2} + 3x\)\( = 3x\left( {{x^2} + 2x + 1} \right)\) \( = 3x{\left( {x + 1} \right)^2}\)

b) \({x^2} – {y^2} – 2x + 2y\)\( = \left( {x – y} \right)\left( {x + y} \right) – 2\left( {x – y} \right)\)\( = \left( {x – y} \right)\left( {x + y – 2} \right)\)

c) \({x^2} – 25 + {y^2} + 2xy\)\( = \left( {{x^2} + 2xy + {y^2}} \right) – 25\)\( = {\left( {x + y} \right)^2} – 25\)\( = \left( {x + y – 5} \right)\left( {x + y + 5} \right)\)

d) \({x^2}\left( {x – 1} \right) + 16\left( {1 – x} \right)\)\( = {x^2}\left( {x – 1} \right) – 16\left( {x – 1} \right)\)\( = \left( {{x^2} – 16} \right)\left( {x – 1} \right)\)\( = \left( {x – 4} \right)\left( {x + 4} \right)\left( {x – 1} \right)\)

e) \(8a\left( {b – c} \right) + 6b\left( {c – b} \right)\)\( = 8a\left( {b – c} \right) – 6b\left( {b – c} \right)\)\( = \left( {b – c} \right)\left( {8a – 6b} \right)\)

f) \({x^2} + 8x + 15\)\( = {x^2} + 3x + 5x + 15\)\( = x\left( {x + 3} \right) + 5\left( {x + 3} \right)\)\( = \left( {x + 5} \right)\left( {x + 3} \right)\)

g) \({x^2} – x – 12\)\( = {x^2} – 4x + 3x – 12\)\( = x\left( {x – 4} \right) + 3\left( {x – 4} \right)\)\( = \left( {x + 3} \right)\left( {x – 4} \right)\)

h) \({\left( {{x^2} + x} \right)^2} + 3\left( {{x^2} + x} \right) + 2\)\( = {\left( {{x^2} + x} \right)^2} + \left( {{x^2} + x} \right) + 2\left( {{x^2} + x} \right) + 2\)\( = \left( {{x^2} + x} \right)\left( {{x^2} + x + 1} \right) + 2\left( {{x^2} + x + 1} \right)\)\( = \left( {{x^2} + x + 1} \right)\left( {{x^2} + x + 2} \right)\)

Bài 4. Tìm x, biết:

a) \(2x\left( {x – 5} \right) – x\left( {3 + 2x} \right) = 26\)

b) \(\left( {4x – 1} \right)\left( {x + 3} \right) – {\left( {2x – 1} \right)^2} = 0\)

c) \(5x\left( {x – 1} \right) = x – 1\)

d) \(2\left( {x + 5} \right) – {x^2} – 5x = 0\)

e) \({\left( {2x – 3} \right)^2} – {\left( {x + 5} \right)^2} = 0\)

f) \(3{x^3} – 48x = 0\)

g) \({x^2} – 6x = – 9\)

h) \({x^2} – x – 6 = 0\)

Phương pháp

Biến đổi biểu thức để tìm x.

Lời giải

a) \(2x\left( {x – 5} \right) – x\left( {3 + 2x} \right) = 26\)

\(\begin{array}{l}2{x^2} – 10x – 3x – 2{x^2} = 26\\ – 13x = 26\\x = – 2\end{array}\)

Vậy x = -2.

b) \(\left( {4x – 1} \right)\left( {x + 3} \right) – {\left( {2x – 1} \right)^2} = 0\)

\(\begin{array}{l}4{x^2} – x + 12x – 3 – \left( {4{x^2} – 4x + 1} \right) = 0\\4{x^2} + 11x – 3 – 4{x^2} + 4x – 1 = 0\\15x – 4 = 0\\15x = 4\\x = \frac{4}{{15}}\end{array}\)

Vậy \(x = \frac{4}{{15}}\).

c) \(5x\left( {x – 1} \right) = x – 1\)

\(\begin{array}{l}5x\left( {x – 1} \right) – \left( {x – 1} \right) = 0\\\left( {5x – 1} \right)\left( {x – 1} \right) = 0\\\left[ \begin{array}{l}5x – 1 = 0\\x – 1 = 0\end{array} \right.\\\left[ \begin{array}{l}x = \frac{1}{5}\\x = 1\end{array} \right.\end{array}\)

Vậy nghiệm của phương trình là \(x \in \left\{ {\frac{1}{5};1} \right\}\).

d) \(2\left( {x + 5} \right) – {x^2} – 5x = 0\)

\(\begin{array}{l}2\left( {x + 5} \right) – x\left( {x + 5} \right) = 0\\\left( {2 – x} \right)\left( {x + 5} \right) = 0\\\left[ \begin{array}{l}2 – x = 0\\x + 5 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 2\\x = – 5\end{array} \right.\end{array}\)

Vậy nghiệm của phương trình là \(x \in \left\{ {2; – 5} \right\}\).

e) \({\left( {2x – 3} \right)^2} – {\left( {x + 5} \right)^2} = 0\)

\(\begin{array}{l}\left( {2x – 3 – x – 5} \right)\left( {2x – 3 + x + 5} \right) = 0\\\left( {x – 8} \right)\left( {3x + 2} \right) = 0\\\left[ \begin{array}{l}x – 8 = 0\\3x + 2 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 8\\x = \frac{{ – 2}}{3}\end{array} \right.\end{array}\)

Vậy nghiệm của phương trình là \(x \in \left\{ {\frac{{ – 2}}{3};8} \right\}\).

f) \(3{x^3} – 48x = 0\)

\(\begin{array}{l}3x\left( {{x^2} – 16} \right) = 0\\3x\left( {x – 4} \right)\left( {x + 4} \right) = 0\\\left[ \begin{array}{l}x = 0\\x = 4\\x = – 4\end{array} \right.\end{array}\)

Vậy nghiệm của phương trình là \(x \in \left\{ { \pm 4;0} \right\}\).

g) \({x^2} – 6x = – 9\)

\(\begin{array}{l}{x^2} – 6x + 9 = 0\\{\left( {x – 3} \right)^2} = 0\\x – 3 = 0\\x = 3\end{array}\)

Vậy x = 3.

h) \({x^2} – x – 6 = 0\)

\(\begin{array}{l}{x^2} + 2x – 3x – 6 = 0\\x\left( {x + 2} \right) – 3\left( {x + 2} \right) = 0\\\left( {x – 3} \right)\left( {x + 2} \right) = 0\\\left[ \begin{array}{l}x = 3\\x = – 2\end{array} \right.\end{array}\)

Vậy nghiệm của phương trình là \(x \in \left\{ {3; – 2} \right\}\).

Bài 5. Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến.

a) \(A = 2xy + \frac{1}{2}x.\left( {2x – 4y + 4} \right) – x\left( {x + 2} \right)\)

b) \(B = {\left( {x + 2} \right)^2} – {\left( {x – 3} \right)^2} – 10x\)

Phương pháp

Sử dụng các phép tính với đa thức và các hằng đẳng thức đáng nhớ biến đổi biểu thức sao cho không còn ẩn.

Lời giải

a) \(A = 2xy + \frac{1}{2}x.\left( {2x – 4y + 4} \right) – x\left( {x + 2} \right)\)

\(\begin{array}{l}A = 2xy + {x^2} – 2xy + 2x – {x^2} – 2x\\A = \left( {2xy – 2xy} \right) + \left( {{x^2} – {x^2}} \right) + \left( {2x – 2x} \right)\\A = 0\end{array}\)

Vì A = 0 nên A không phụ thuộc vào biến x, y.

b) \(B = {\left( {x + 2} \right)^2} – {\left( {x – 3} \right)^2} – 10x\)

\(\begin{array}{l}B = \left( {x + 2 – x + 3} \right)\left( {x + 2 + x – 3} \right) – 10x\\B = 5\left( {2x – 1} \right) – 10x\\B = 10x – 5 – 10x\\B = – 5\end{array}\)

Vì B = -5 nên B không phụ thuộc vào biến x, y.

Bài 6. Thống kê trong lần kiểm tra cuối học kì I của lớp 8A vừa qua là:

a) Tính tổng số bài kiểm tra cuối học kì I của lớp 8A.

b) Số bài được điểm 10 chiếm bao nhiêu phần trăm so với tổng số bài kiểm tra cuối học kì I của lớp 8A?

Phương pháp

a) Tính tổng số bài.

b) Tính số phần trăm bài được điểm 10 = số bài được điểm 10 : tổng số bài . 100

Lời giải

a) Tổng số bài kiểm tra cuối học kì I của lớp 8A là:

6 + 7 + 6 + 7 + 4 + 7 + 5 = 42 (bài)

Vậy lớp 8A có 42 bài kiểm tra cuối học kì I.

b) Số bài được điểm 10 chiếm số phần trăm là:

\(\frac{5}{{42}}.100\% \approx 12\% \)

Vậy số bài được điểm 10 chiếm khoảng 12% so với tổng số bài kiểm tra cuối học kì I của lớp 8A.

Bài 7. Cho biểu đồ về lượng mưa và nhiệt độ trong năm 2022 của Hà Nội

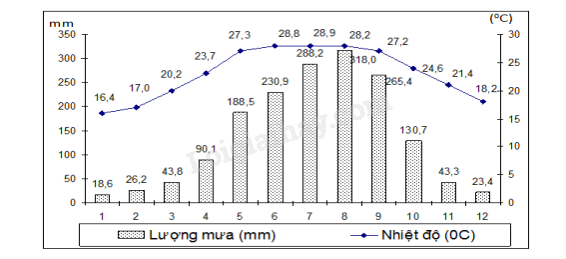
a) Tháng nào có nhiệt độ cao nhất, thấp nhất? Vì sao lại có sự khác biệt này?

b) Tháng nào có lượng mưa nhiều nhất, ít nhất?

c) Em thích tháng nào nhất trong năm và tháng đó có nhiệt độ và lượng mưa như thế nào?

Phương pháp

Quan sát biểu đồ để trả lời.

Lời giải

a) Quan sát biểu đồ, ta thấy:

– Tháng có nhiệt độ cao nhất là tháng 7 (28,9⁰C).

– Tháng có nhiệt độ thấp nhất là tháng 1 (16,4⁰C).

Sự khác biệt về nhiệt độ này có vì Hà Nội nằm ở miền Bắc, có sự thay đổi thời tiết rõ ràng mùa nóng và mùa lạnh.

b) Quan sát biểu đồ, ta thấy:

– Tháng có lượng mưa nhiều nhất là tháng 8 (318,0mm)

– Tháng có lượng mưa ít nhất là tháng 1 (18,6mm)

c) Học sinh tự lựa chọn tháng mình thích và liệt kê nhiệt độ và lượng mưa của tháng đó.

Bài 8. Biểu đồ hình quạt tròn ở hình bên biểu diễn tỉ lệ các yếu tố ảnh hưởng đến sinh trưởng của cây trồng như: Phân bón; Nước tưới; Giống; Kiểm soát dịch hại; Kiểm soát cỏ dại; Yếu tố khác.

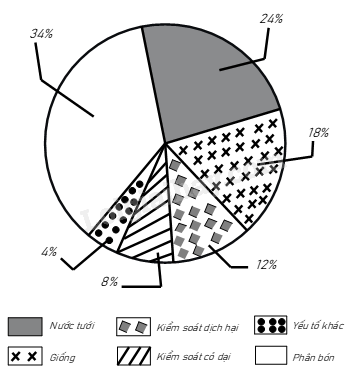
a) Cho biết yếu tố nào ảnh hưởng đến sinh trưởng của cây trồng nhiều nhất?

b) Trong các yếu tố ảnh hưởng đến sinh trưởng của cây thì yếu tố kiểm soát dịch hại gấp mấy lần yếu tố khác?

Phương pháp

Quan sát biểu đồ để trả lời.

Lời giải

a) Quan sát biểu đồ, ta thấy yếu tố ảnh hưởng đến sinh trưởng của cây trồng nhiều nhất là phân bón (34%).

b) Ta có tỉ lệ phần trăm của yếu tố kiểm soát dịch hại là 12%.

Tỉ lệ phần trăm của yếu tố khác là 4%.

Yếu tố kiểm soát dịch hại gấp yếu tố khác là: \(\frac{{12\% }}{{4\% }} = 3\) (lần)

Bài 9. Cho hình thang ABCD (AB // CD), M là trung điểm của CD. Gọi E là giao điểm của AC và BM, F là giao điểm của BD và AM. Đường thẳng EF cắt BC và AD lần lượt tại G và H.

a) Chứng minh rằng \(\frac{{EA}}{{EC}} = \frac{{2AB}}{{CD}}\).

b) Chứng minh rằng EF // CD.

c) Chứng minh rằng GE = EF = FH.

Phương pháp

Sử dụng định lí Thales để chứng minh.

Lời giải

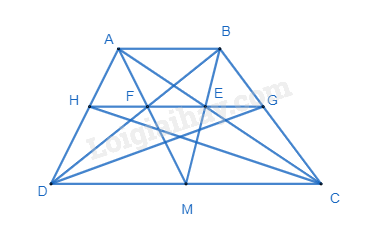
a) Vì AB // CM nên \(\frac{{AE}}{{EC}} = \frac{{AB}}{{CM}}\) (theo định lí Thales)

\( \Leftrightarrow \frac{{AE}}{{EC}} = \frac{{AB}}{{\frac{1}{2}CD}}\)(vì M là trung điểm của CD)

\( \Leftrightarrow \frac{{AE}}{{EC}} = \frac{{2AB}}{{CD}}\) (đpcm). (1)

b) Chứng minh tương tự như phần a, ta có: \(\frac{{AF}}{{FM}} = \frac{{AB}}{{DM}} = \frac{{2AB}}{{CD}}\)(2)

Từ (1) và (2) suy ra \(\frac{{AE}}{{EC}} = \frac{{AF}}{{FM}} \Rightarrow EF//CM\) hay EF // CD (đpcm).

c) Ta có EF // CD => EF // AB (vì AB // CD)

Áp dụng định lí Thales, ta có:

\(\left. \begin{array}{l}HF//DM \Rightarrow \frac{{AF}}{{AM}} = \frac{{HF}}{{DM}}\\EF//CM \Rightarrow \frac{{AF}}{{AM}} = \frac{{EF}}{{CM}}\\CM = DM\end{array} \right\} \Rightarrow HF = EF\)

Áp dụng định lí Thales, ta có:

\(\left. \begin{array}{l}EG//CM \Rightarrow \frac{{BE}}{{BM}} = \frac{{EG}}{{CM}}\\EF//DM \Rightarrow \frac{{BE}}{{BM}} = \frac{{EF}}{{DM}}\\CM = DM\end{array} \right\} \Rightarrow EG = EF\)

Suy ra GE = EF = FH. (đpcm)

Bài 10. Cho hình bình hành ABCD, M là trung điểm của AB. Gọi G là giao điểm của AC và DM. Lấy điểm E thuộc đoạn thẳng AM. Các đường thẳng GE và CD cắt nhau tại F.

a) Chứng minh rằng G là trọng tâm của tam giác ABD.

b) Chứng minh rằng GC = 2GA.

c) Kẻ đường thẳng qua G cắt các cạnh AD và BC lần lượt tại I và K. Chứng minh rằng EI // KF.

d) Gọi N là trung điểm của AD. Chứng minh rằng BF = 2EN.

Phương pháp

a) Chứng minh G là giao điểm của các đường trung tuyến trong tam giác ABD.

b) Sử dụng tính chất của trọng tâm trong tam giác.

c) \(\frac{{IG}}{{GK}} = \frac{{EG}}{{GF}} \Rightarrow IE//FK\)

d) Sử dụng tính chất đường trung tuyến, chứng minh GB = 2NG.

Chứng minh \(\frac{{NG}}{{GB}} = \frac{{EG}}{{GF}} \Rightarrow NE//BF \Rightarrow BF = 2NE\)

Lời giải

a) Gọi O là giao điểm của AC và BD. Khi đó O là trung điểm của AC và BD.

Ta có O và M lần lượt là giao điểm của BD và AB. Xét tam giác ABD, ta có:

AO và DM là các đường trung tuyến và G là giao điểm cua AO và DM. Suy ra G là trọng tâm của tam giác ABD (đpcm).

b) Ta có G là trọng tâm của tam giác ABD nên \(AG = \frac{2}{3}AO\).

Mà O là trung điểm của AC nên \(AO = \frac{1}{2}AC\).

Suy ra \(AG = \frac{2}{3}AO = \frac{2}{3}.\frac{1}{2}AC = \frac{1}{3}AC\)

\( \Rightarrow GC = AC – AG = AC – \frac{1}{3}AC = \frac{2}{3}AC\)

\( \Rightarrow \frac{{GC}}{{AG}} = \frac{{\frac{2}{3}AC}}{{\frac{1}{3}AC}} = 2\) hay \(GC = 2AG\)(đpcm).

c) Ta có:

+) AI // CK (Do AD // BC) \( \Rightarrow \frac{{AG}}{{GC}} = \frac{{IG}}{{GK}}\) (Theo định lí Thales)

+) AE // CF (Do AB // CD) \( \Rightarrow \frac{{AG}}{{GC}} = \frac{{EG}}{{GF}}\) (Theo định lí Thales)

Suy ra \(\frac{{IG}}{{GK}} = \frac{{EG}}{{GF}} \Rightarrow IE//FK\) (Định lí Thales đảo) (đpcm)

d) Ta có N là trung điểm của AD nên BN là đường trung tuyến của tam giác ABD suy ra \(BG = \frac{2}{3}BN,NG = \frac{1}{3}BN\).

Do đó: \(\frac{{GB}}{{NG}} = \frac{{\frac{2}{3}BN}}{{\frac{1}{3}BN}} = 2\).

Tương tự phần c, ta chứng minh:

AN // BC \( \Rightarrow \frac{{AG}}{{GC}} = \frac{{NG}}{{GB}}\)

\(\frac{{AG}}{{GC}} = \frac{{EG}}{{GF}}\) (cmt)

\( \Rightarrow \frac{{NG}}{{GB}} = \frac{{EG}}{{GF}} \Rightarrow NE//BF\)(Định lí Thales đảo)

\( \Rightarrow \frac{{BF}}{{NE}} = \frac{{GB}}{{GN}} = 2\) hay \(BF = 2NE\)(đpcm)

Bài 11. Cho hình vuông ABCD có tâm O, gọi E là trung điểm của AB, DE cắt AC tại F, BF cắt CD tại I.

a) Chứng minh D là trung điểm của IC.

b) Chứng minh ABDI là hình bình hành.

c) Gọi H là trung điểm của AI, CH cắt BD tại L. Chứng minh L là trung điểm của OD.

Phương pháp

a) Để chứng minh D là trung điểm của IC, ta cần chứng minh DI = IC. Chứng minh các tam giác bằng nhau để suy ra DI = IC.

b) Chứng minh ABDI là tứ giác có cặp cạnh đối song song và bằng nhau.

c) Dựa vào tính chất của đường trung bình, chứng minh OD là đường trung bình của tam giác ACI, OL là đường trung bình của tam giác ACH suy ra OL = \(\frac{1}{2}\) OD hay L là trung điểm của OD.

Lời giải

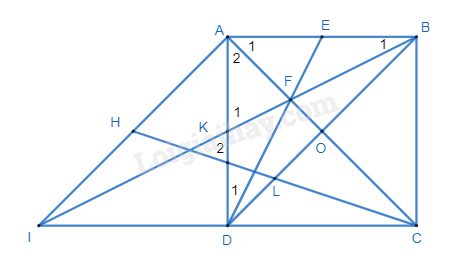
a) Gọi K là giao điểm của BF và AD.

Xét tam giác ABF và tam giác ADF có:

AB = AD (ABCD là hình vuông)

\(\widehat {{A_1}} = \widehat {{A_2}}\)(Vì AF là tia phân giác của góc BAD)

AF chung

\( \Rightarrow \Delta ABF = \Delta ADF\left( {c.g.c} \right)\)

\( \Rightarrow \widehat {{B_1}} = \widehat {{D_1}}\) (hai góc tương ứng)

Xét tam giác ABK và tam giác ADE có:

\(\widehat A\) chung

AB = AD

\(\widehat {{B_1}} = \widehat {{D_1}}\)(cmt)

\( \Rightarrow \Delta ABK = \Delta ADE\)(g.c.g)

\( \Rightarrow AE = AK\)(hai cạnh tương ứng).

Mà E là trung điểm của AB nên AE = EB = \(\frac{1}{2}\)AB

\( \Rightarrow AK = \frac{1}{2}AB = \frac{1}{2}AD\) (vì AB = AD), mà \(K \in AD\)nên K là trung điểm của AD \( \Rightarrow AK = KD\)

Xét tam giác ABK và tam giác DIK có:

\(\widehat A = \widehat D\left( { = {{90}^0}} \right)\)

AK = KD

\(\widehat {{K_1}} = \widehat {{K_2}}\)

\( \Rightarrow \Delta ABK = \Delta DIK\)(g.c.g)

\( \Rightarrow ID = AB\)(2 cạnh tương ứng)

Mà AB = DC

\( \Rightarrow ID = DC\) hay D là trung điểm của IC. (đpcm)

b) Xét tứ giác ABDI có:

AB // ID (do AB // CD)

AB = DI (cmt)

=> ABDI là hình bình hành (đpcm)

c) Xét tam giác ACI có:

O là trung điểm của AC (O là giao điểm của hai đường chéo trong hình vuông)

D là trung điểm của IC (cmt)

=> OD là đường trung bình của tam giác ACI

\( \Rightarrow OD = \frac{1}{2}AI = AH\)(1)

Xét tam giác ACH có:

O là trung điểm của của AC

OL // AH

=> OL là đường trung bình của tam giác ACH

\( \Rightarrow OL = \frac{1}{2}AH\)(2)

Từ (1) và (2) suy ra \(OL = \frac{1}{2}OD\) hay L là trung điểm của OD (đpcm)

Bài 12. 

Để làm cây thông noel, người thợ sẽ dùng một cái khung sắt hình tam giác cân như hình vẽ bên, sau đó gắn mô hình cây thông lên. Cho biết thanh BC = 120cm. Tính độ dài các thanh GF; HE; ID.

Phương pháp

Sử dụng tính chất của đường trung bình trong tam giác, định lí thales đảo để tính.

Lời giải

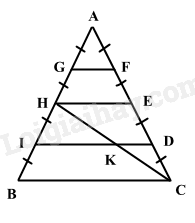
Ta có: AG = GH = HI = IB = AF = FE = ED = DC

Suy ra AH = HB = AE = EC hay H là trung điểm của AB; E là trung điểm của AC.

Xét tam giác ABC có: AH = HB (vì AG + GH = HI + BI), AE = EC (vì AF + FE = ED + DC) suy ra HE là đường trung bình của tam giác ABC.

\( \Rightarrow HE = \frac{1}{2}BC = \frac{1}{2}.120 = 60\left( {cm} \right)\)

Xét tam giác AHE có AG = GH; AF = FE suy ra GF là đường trung bình của tam giác AHE.

\( \Rightarrow GF = \frac{1}{2}HE = \frac{1}{2}.60 = 30\left( {cm} \right)\)

Xét tam giác ABC có: \(\frac{{AI}}{{IB}} = \frac{{AD}}{{DC}}\left( {AG + GH + HI = AF + FE + ED} \right) \Rightarrow ID//BC\) (định lí Thales đảo)

Gọi K là giao điểm của CH và ID.

Xét tam giác HBC có: HI = IB (gt), IK // BC nên IK là đường trung bình của tam giác HBC

\( \Rightarrow IK = \frac{1}{2}BC = \frac{1}{2}.120 = 60\left( {cm} \right)\)

Xét tam giác CEH có: ED = DC (gt), DK // HE nên DK là đường trung bình của tam giác CEH

\( \Rightarrow DK = \frac{1}{2}HE = \frac{1}{2}.60 = 30\left( {cm} \right)\)

\( \Rightarrow DI = DK + KI = 30 + 60 = 90\left( {cm} \right)\)

Vậy độ dài thanh GF 30cm; HE = 60cm; ID = 90cm. 

Bài 13*. Tính GTNN của biểu thức \(B = {x^2} + 2{y^2} + 3{z^2} – 2xy + 2xz – 2x – 2y – 8z + 2000\).

Phương pháp

Sử dụng hằng đẳng thức đáng nhớ nâng cao.

Lời giải

Ta có:

\(\begin{array}{l}B = {x^2} + 2{y^2} + 3{z^2} – 2xy + 2xz – 2x – 2y – 8z + 2000\\ = \left( {{x^2} + {y^2} + {z^2} + 1 + 2z – 2y – 2z – 2xy + 2xz – 2yz} \right) + \left( {{y^2} + {z^2} + 4 + 2yz – 2y – 4z} \right) + \left( {{z^2} – 2z + 1} \right) + 1996\\ = {\left( {x + y + z – 1} \right)^2} + {\left( {y + z – 2} \right)^2} + {\left( {z – 1} \right)^2} + 1996 \ge 1996\,\,\forall x,y,z\end{array}\)

vì \(\left\{ \begin{array}{l}{\left( {x – y + z – 1} \right)^2} \ge 0\,\,\forall x,y,z\\{\left( {y + z – 2} \right)^2} \ge 0\,\forall y,z\\{\left( {z – 1} \right)^2} \ge 0\,\forall z\end{array} \right.\)

Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}{\left( {x – y + z – 1} \right)^2} = 0\\{\left( {y + z – 2} \right)^2} = 0\\{\left( {z – 1} \right)^2} = 0\end{array} \right.\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x – y + z = 1\\y + z = 2\\z = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x – y + 1 = 1\\y + 1 = 2\\z = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1\\z = 1\end{array} \right.\end{array}\)

Vậy MinB = 1996 khi x = 1; y = 1; z = 1.

Bài 14*. Cho a + b = 1. Tính giá trị của biểu thức sau:

\(M = {a^3} + {b^3} + 3ab\left( {{a^2} + {b^2}} \right) + 6{a^2}{b^2}\left( {a + b} \right)\).

Phương pháp

Biến đổi biểu thức thành biểu thức chứa a + b để rút gọn.

Lời giải

Ta có:

Thay a + b = 1 và biến đổi M, ta được:

\(M = {a^3} + {b^3} + 3ab\left( {{a^2} + {b^2}} \right) + 6{a^2}{b^2}\left( {a + b} \right)\)

\(\begin{array}{l} = \left( {a + b} \right)\left( {{a^2} – ab + {b^2}} \right) + 3ab\left( {{a^2} + {b^2}} \right) + 6{a^2}{b^2}.1\\ = {a^2} – ab + {b^2} + 3ab\left( {{a^2} + {b^2}} \right) + 6{a^2}{b^2}\\ = {a^2} + {b^2} – ab + 3ab\left( {{a^2} + {b^2} + 2ab} \right)\\ = {a^2} + {b^2} – ab + 3ab{\left( {a + b} \right)^2}\\ = {a^2} + {b^2} – ab + 3ab\\ = {a^2} + {b^2} + 2ab\\ = {\left( {a + b} \right)^2} = 1\end{array}\)

Vậy với a + b = 1 thì M = 1.