Đề bài
Câu 1: Tìm điều kiện xác định của biểu thức \(\dfrac{1}{{\sqrt[3]{{x – 3}}}}\)
A. \(x \ne 3.\) B. \(x \ge 3.\) C. \(x\, > 3\). D. \(x < 3.\)
Câu 2: Cho hàm số \(y = 3{x^2}.\) Kết luận nào sau đây đúng?
A. Hàm số đồng biến khi \(x < 0,\) nghịch biến khi \(x > 0.\)
B. Hàm số luôn nghịch biến trên \(\mathbb{R}\).
C. Hàm số đồng biến trên \(\mathbb{R}\).
D. Hàm số nghịch biến khi \(x < 0\), đồng biến khi \(x > 0.\)
Câu 3: Phương trình \(2x + 3y = 5\) nhận cặp số nào sau đây là một nghiệm?
A. \(\left( { – 1;1} \right)\). B. \(\left( {1; – 1} \right)\). C. \(\left( { – 1; – 1} \right)\). D. \(\left( {1;1} \right)\).
Câu 4: Trong đường tròn \(\left( {O;\,4cm} \right)\), dây lớn nhất có độ dài bằng
A. \(10cm.\) B. \(8cm.\) C. \(4cm.\) D. \(6cm.\)
Câu 5: Cho \(\Delta MNP\) vuông tại \(M\), đường cao \(MH\). Khẳng định nào sau đây đúng?
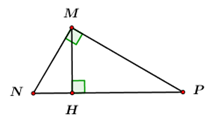
A. \(\dfrac{1}{{M{H^2}}} = \dfrac{1}{{M{N^2}}}.\dfrac{1}{{M{P^2}}}.\) B. \(\dfrac{1}{{M{H^2}}} = \dfrac{1}{{M{N^2}}} – \dfrac{1}{{M{P^2}}}.\)
C. \(\dfrac{1}{{M{H^2}}} = \dfrac{1}{{M{N^2}}} + \dfrac{1}{{M{P^2}}}.\) D. \(\dfrac{1}{{M{H^2}}} = \dfrac{1}{{MN}} + \dfrac{1}{{MP}}.\)
Câu 6: Cho hai đường tròn \(\left( {O;\,R} \right)\) và \(\left( {I;\,r} \right)\) với \(\left( {R > r} \right)\) tiếp xúc trong với nhau khi đó ta có:
A. \(OI = R – r\). B. \(OI = R + r\). C. \(R – r < OI < R + r\). D. \(OI > R + r\).
Câu 7: Trong hình vẽ bên, \(\sin C\) bằng
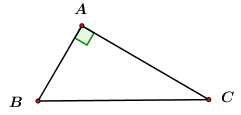
A. \(\dfrac{{AC}}{{BC}}\). B. \(\dfrac{{AC}}{{AB}}\). C. \(\dfrac{{AB}}{{BC}}\). D. \(\dfrac{{AB}}{{AC}}\).
Câu 8: Tìm \(m\) và \(n\) để \(\left( {x;y} \right) = \left( {1;1} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x + my = 3\\nx + 2y = 5\end{array} \right..\)
A. \(m = 1;n = 1.\) B. \(m = 1;n = 3.\) C. \(m = – 1;n = 3.\) D. \(m = – 1;n = 1.\)
Câu 9: Có bao nhiêu tứ giác nội tiếp được đường tròn trong các hình vẽ dưới đây?
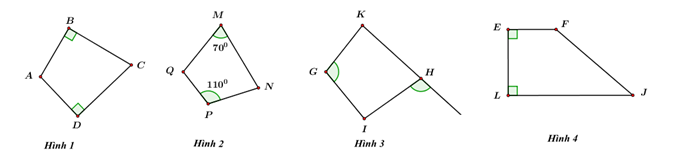
A. \(3.\) B. \(4.\) C. \(1.\) D. \(2.\)
Câu 10: Trong các hàm số sau, hàm số nào là hàm số bậc nhất?
A. \(y = – 4x + 3.\) B. \(y = 2 + \dfrac{1}{x}.\) C. \(y = \sqrt x + 3.\) D. \(y = 2{x^2}.\)
Câu 11: Tìm \(m\) để phương trình \({x^2} + 2\left( {m – 2} \right)x + m – 3 = 0\) có hai nghiệm trái dấu.
A. \(m \le 3.\) B. \(m \ge 3.\) C. \(m > 3.\) D. \(m < 3.\)
Câu 12: Gọi \(\left( {{x_0};{y_0}} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + 3y = – 7\\x + 2y = – 4\end{array} \right.\). Tính \(S = {x_0} + {y_0}.\)
A. \(S = – 5.\) B. \(S = – 1.\) C. \(S = 1.\) D. \(S = 5.\)
Câu 13: Trong hình vẽ bên, với đường tròn \(\left( O \right)\) thì \(\angle ABC\) là
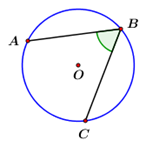
A. góc nội tiếp. B. góc có đỉnh ở bên trong đường tròn.
C. góc tạo bởi tia tiếp tuyến và dây cung. D. góc ở tâm.
Câu 14: Tổng hai nghiệm của phương trình \({x^2} – 5x – 7 = 0\) bằng
A. \( – 7\) B. \(5.\) C. \(7.\) D. \( – 5.\)
Câu 15: Thể tích hình cầu có bán kính \(r = 5cm\) là
A. \(100\,\pi c{m^2}\). B. \(25\pi c{m^2}.\) C. \(\dfrac{{500\pi }}{3}c{m^2}.\) D. \(\dfrac{{100\pi }}{3}c{m^2}.\)
Câu 16: Tìm \(m\) để hàm số \(y = \left( {m + 2} \right)x – 5\) đồng biến trên \(\mathbb{R}\).
A. \(m > – 2.\) B. \(m = – 2.\) C. \(m \ne – 2.\) D. \(m < – 2.\)
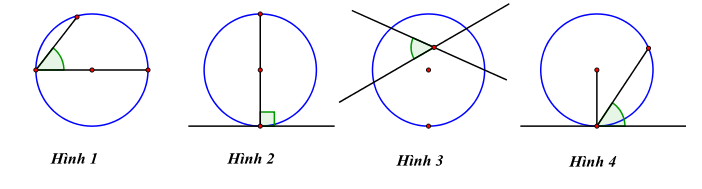
Câu 17: Trong các hình vẽ dưới đấy, hình nào vẽ góc có đỉnh bên trong đường tròn?
Câu 18: Hình trụ có bán kính đáy \(r,\) chiều cao \(h\) thì diện tích xung quanh là
A. \(\pi rh.\) B. \(\frac{1}{3}\pi {r^2}h.\) C. \(2\pi rh.\) D. \(\pi {r^2}h.\)
Câu 19: Giá trị của hàm số \(y = 2{x^2}\) tại \(x = 3\) là
A. \(9\) B. \(12\) C. \(18\) D. \(6\)
Câu 20: Với \(a > b\), biểu thức \(\frac{1}{{a – b}}.\sqrt {{4^2}{{\left( {a – b} \right)}^2}} \) có kết quả rút gọn là
A. \( – 2\). B. \(4.\) C. \(2.\) D. \( – 4.\)
Câu 21: Trong hình vẽ bên, biết sđ và sđ. Số đo \(\angle AED\) bằng
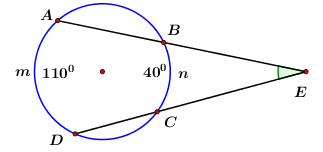
A. \({55^0}\). B. \({75^0}.\) C. \({35^0}.\) D. \({70^0}.\)
Câu 22: Gọi \({x_1};\,{x_2}\) là hai nghiệm của phương trình \({x^2} – 2x – 2 = 0\). Tính \(T = {x_1} + {x_2} + 2{x_1}{x_2}.\)
A. \(T = – 5.\) B. \(T = – 6.\) C. \(T = – 2.\) D. \(T = – 3.\)
Câu 23: Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\), biết \(\angle DBC = {80^0}\), khi đó \(\angle DAC\) bằng
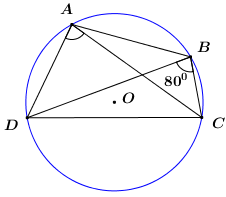
A. \({50^0}\). B. \({160^0}.\) C. \({40^0}.\) D. \({80^0}.\)
Câu 24: Tìm điều kiện xác định của biểu thức \(\sqrt {x – 2} .\)
A. \(x \ge – 2\). B. \(x < 2.\) C. \(x \le 2.\) D. \(x \ne 2.\)
Câu 25: Trong các hệ phương trình sau đây, hệ phương trình nào có vô số nghiệm?
A. \(\left\{ \begin{array}{l}x – y = 1\\3x – 3y = 2\end{array} \right.\). B. \(\left\{ \begin{array}{l}5x – 3y = 1\\5x + 2y = 2\end{array} \right.\) C. \(\left\{ \begin{array}{l}3x – 2y = 5\\6x – 4y = 10\end{array} \right.\) D. \(\left\{ \begin{array}{l}3x – 2y = 5\\5x – 3y = 1\end{array} \right.\)
Câu 26: Nếu \(\sqrt {3 + \sqrt x } = 4\) thì \(x\) bằng
A. \(1\). B. \(13.\) C. \(169.\) D. \(\sqrt {13} .\)
Câu 27: Có bao nhiêu đường tròn đi qua 3 điểm phân biệt không thẳng hàng?
A. Vô số đường tròn. B. Một đường tròn.
C. Hai đường tròn. D. Không có đường tròn nào.
Câu 28: Tìm \(a\) để điểm \(M\left( { – 1;2} \right)\) thuộc đồ thị hàm số \(y = a{x^2}\,\left( {a \ne 0} \right).\)
A. \(a = \frac{{ – 1}}{4}.\). B. \(a = 2.\) C. \(a = \frac{{ – 1}}{2}.\) D. \(a = – 2.\)
Câu 29: Với góc nhọn \(\alpha \) tùy ý, khẳng định nào sau đây là Sai?
A. \(\tan \,\alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\) B. \(\tan \,\alpha .\cot \alpha = 1.\) C. \(\cot \,\alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\) D. \({\sin ^2}\alpha + \cos {\,^2}\alpha = 1.\)
Câu 30: Thể tích hình nón có chiều cao \(h = 5cm,\) bán kính đáy \(r = 3cm\) bằng
A. \(45\pi c{m^2}.\). B. \(9\pi c{m^2}.\) C. \(15\pi c{m^2}.\) D. \(60\pi c{m^2}.\)
Câu 31: Trong các hàm số sau, hàm số nào nghịch biến trên \(\mathbb{R}\)?
A. \(y = 2x – 7.\) B. \(y = – 3x + 5.\) C. \(y = – 2{x^2}.\) D. \(y = 5{x^2}.\)
Câu 32: Biệt thức \(\Delta ‘\) của phương trình \(3{x^2} – 2mx – 1 = 0\) là
A. \({m^2} + 3.\) B. \(4{m^2} + 12\). C. \({m^2} – 3.\) D. \(4{m^2} – 12.\)
Câu 33: Phương trình nào sau đây là phương trình bậc nhất hai ẩn \(x,y?\)
A. \(2x – 5y = 3.\) B. \(2x + 3\sqrt y = 0.\) C. \(2{x^2} – 4xy + {y^2} = 0\) D. \(4x + \frac{1}{y} = 3.\)
Câu 34: Đường thẳng nào sau đây song song với đường thẳng \(y = – 2x + 3?\)
A. \(y = – 2x + 7\). B. \(y = – 3x + 2\) C. \(y = 3x + 8\) D. \(y = 2x + 1\)
Câu 35: Giá tị của biểu thức \(A = 3\sqrt {80} – 2\sqrt {20} \) bằng
A. \(2\sqrt 5 .\) B. \(8\sqrt 5 .\) C. \(\sqrt {60} .\) D. \(16\sqrt 5 .\)
Câu 36: Cho \(a > 0;\,b > 0\) và \(S = \,2{a^2} + {b^2} + \frac{4}{a} + \frac{{54}}{b}.\) Khi biểu thức \(S\) đạt giá trị nhỏ nhất thì \(T = a + 2b\) có giá trị bằng
A. \(7.\) B. \(3.\) C. \(6.\) D. \(5.\)
Câu 37: Tìm \(m\) để hệ phương trình \(\left\{ \begin{array}{l}2x + y = 3m\\x – y = – 9\end{array} \right.\) có nghiệm \(\left( {x;y} \right)\) thỏa mãn \(x > 0\) và \(y > 0\).
A. \(m < – 6.\) B. \(m < – 3\). C. \(m > 3.\) D. \(m > – 6.\)
Câu 38: Giá trị nhỏ nhất của \(y = 4 + \sqrt {3{x^2} – 6x + 7} \) bằng
A. \(4\). B. \(4 + \sqrt 7 \). C. \(6\). D. \(4 + \sqrt 6 \).
Câu 39: Một bồn cây có dạng hình tròn bán kính \(1m\). Do yêu cầu mở rộng diện tích mà bồn cây được mở rộng bằng cách tăng bán kính thêm \(0,6m.\) Tính diện tích tăng thêm của bồn cây đó (lấy \(\pi \approx 3,14\) và kết quả làm tròn đến một chữ số thập phân).
A. \(4,8{m^2}.\) B. \(3,8{m^2}.\) C. \(1,9{m^2}.\) D. \(4,9{m^2}.\)
Câu 40: Gọi \(A,\,B\) lần lượt là giao điểm của đường thẳng \(y = 2x + 4\) với hai trục tọa độ \(Ox,\,Oy.\) Diện tích tam giác \(AOB\) bằng
A. \(6.\) B. \(2.\) C. \(4.\) D. \(8.\)
Câu 41: Khoảng cách lớn nhất từ gốc tọa độ \(O\) đến đường thẳng \(\left( d \right):y = \left( {m – 1} \right)x + 4m\) là
A. \(2\sqrt 2 .\) B. \(8\sqrt 2 .\) C. \(4\sqrt 2 \). D. \(4.\)
Câu 42: Một người mua hai thùng hàng \(A\) và \(B\). Nếu thùng hàng \(A\) tăng giá \(20\% \) và thùng hàng \(B\) tăng \(30\% \) thì người đó phải trả \(302\) nghìn đồng. Nếu thùng hàng \(A\) giảm giá \(10\% \) và thùng hàng \(B\) giảm giá \(20\% \) thì người đó phải trả \(202\) nghìn đồng. Giá tiền thùng hàng \(A\) và thùng hàng \(B\) lúc đầu lần lượt là
A. 20 nghìn đồng, 230 nghìn đồng. B. 100 nghìn đồng, 140 nghìn đồng.
C. 140 nghìn đồng, 100 nghìn đồng. D. 230 nghìn đồng, 20 nghìn đồng.
Câu 43: Có bao nhiêu giá trị của \(x\) để \(A = \frac{{4\sqrt x + 16}}{{\sqrt x + 2}}\) (với \(x \ge 0\)) nhận giá trị nguyên?
A. \(6.\) B. \(4.\) C. \(8.\) D. \(3.\)
Câu 44: Cho hai nửa đường tròn đường kính \(AB\) và \(BC\) tiếp xúc nhau tại \(B\) (xem hình vẽ bên), biết \(AB = BC = 18,\,CD\) cắt nửa đường tròn \(\left( {O’} \right)\) tại \(E,\) gọi \(H\) là trung điểm của \(CE,\,F\) là điểm chính giữa của cung . Tính \(HF.\)
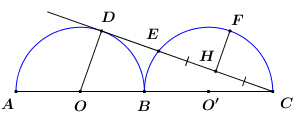
A. \(HF = 2.\) B. \(HF = 6.\) C. \(HF = 12.\) D. \(HF = 3.\)
Câu 45: Cho tam giác \(MNP\) cân tại \(M,\) đường cao \(MI\) và \(NK\) cắt nhau tại \(O.\) Đường tròn \(\left( {O;\,OK} \right)\) cắt \(MI\) tại \(G\) và \(E\) (tham khảo hình vẽ bên). Biết \(MN = MP = \sqrt 3 \) và \(MG = EI.\) Tính \(OK.\)
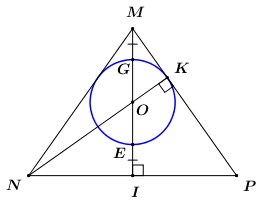
A. \(OK = \frac{{\sqrt 6 }}{3}.\) B. \(OK = \frac{{\sqrt 6 }}{6}.\) C. \(OK = \frac{{\sqrt 6 }}{2}.\) D. \(OK = \sqrt 6 .\)
Câu 46: Trong hình vẽ bên, tam giác \(ABC\) vuông tại \(A,\) cạnh \(AB = 5cm,\) đường cao \(AH = 3cm.\) Độ dài cạnh \(BC\)bằng
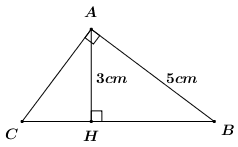
A. \(\frac{4}{{15}}\,cm.\) B. \(4cm.\) C. \(\frac{{25}}{4}cm.\) D. \(\frac{{25}}{{16}}cm.\)
Câu 47: Một học sinh dùng kế giác, đứng cách chân cột cờ \(10m\) rồi chỉnh mặt thước ngắm cao bằng mắt của mình để xác định góc “nâng” (góc tạo bởi tia sáng đi thẳng từ đỉnh cột cờ với mắt tạo với phương nằm ngang). Khi đó, góc “nâng” đo được \({31^0}\). Biết khoảng cách từ mặt sân đến mắt học sinh đó bằng \(1,5m\). Tính chiều cao cột cờ (kết quả làm tròn đến một chữ số thập phân).
A. \(6,0m.\) B. \(16,6m.\) C. \(7,5m.\) D. \(5,0m.\)
Câu 48: Gọi \(S\) là tập các giá trị của \(m\) để đường thẳng \(y = mx + 3\) cắt trục \(Ox\) và trục \(Oy\) lần lượt tại \(A\) và \(B\) sao cho tam giác \(AOB\) cân. Tính tổng các phần tử của \(S.\)
A. \(1.\) B. \(3.\) C. \( – 1.\) D. \(0.\)
Câu 49: Tìm \(m\) để đường thẳng \(\left( d \right):y = x + m – 1\) cắt parabol \(\left( P \right):y = \frac{1}{2}{x^2}\) tại 2 điểm \(A\) và \(B\) sao cho \(\Delta AOB\) vuông tại \(O\) (với \(O\) là gốc tọa độ).
A. \(m = 3.\) B. \(m = 1;m = 3.\) C. \(m = – 1;m = – 3.\) D. \(m = 1\)
Câu 50: Cho đường tròn \(\left( {O;\,10cm} \right)\), dây \(CD\) cách tâm \(O\) một khoảng bằng \(8cm\). Khi đó độ dài đáy \(CD\) là
A. \(6cm.\) B. \(2\sqrt {41} cm.\) C. \(12cm.\) D. \(2\sqrt {21} cm.\)
Lời giải chi tiết
|
1. A
|
2. D
|
3. D
|
4. B
|
5. C
|
6. A
|
7. C
|
8. B
|
9. A
|
10. A
|
|
11. D
|
12. B
|
13. A
|
14. B
|
15. C
|
16. A
|
17. D
|
18. C
|
19. C
|
20. B
|
|
21. C
|
22. C
|
23. D
|
24. A
|
25. C
|
26. C
|
27. B
|
28. B
|
29. A
|
30. C
|
|
31. B
|
32. A
|
33. A
|
34. A
|
35. B
|
36. A
|
37. C
|
38. C
|
39. D
|
40. C
|
|
41. C
|
42. B
|
43. B
|
44. B
|
45. B
|
46. C
|
47. C
|
48. D
|
49. A
|
50. C
|
Câu 1 – Căn bậc ba
Phương pháp:
– Biểu thức \(\dfrac{1}{A}\) xác định khi \(A \ne 0\).
– Biểu thức \(\sqrt[3]{A}\) xác định với mọi \(A\).
Cách giải:
Biểu thức \(\dfrac{1}{{\sqrt[3]{{x – 3}}}}\) xác định khi và chỉ khi \(x – 3 \ne 0 \Leftrightarrow x \ne 3\).
Chọn A.
Câu 2 – Hàm số y = ax^2 (a ≠ 0)
Phương pháp:
Hàm số \(y = a{x^2}\,\,\left( {a \ne 0} \right)\).
– Nếu \(a > 0\) thì hàm số đồng biến khi \(x > 0\), nghịch biến khi \(x < 0\).
– Nếu \(a < 0\) thì hàm số đồng biến khi \(x < 0\), nghịch biến khi \(x > 0\).
Cách giải:
Hàm số \(y = 3{x^2}\) có \(a = 3 > 0\) nên hàm số nghịch biến khi \(x < 0\), đồng biến khi \(x > 0\).
Chọn D.
Câu 3 – Phương trình bậc nhất hai ẩn
Phương pháp:
Thay các cặp số ở các đáp án vào phương trình \(2x + 3y = 5\).
Cách giải:
– Đáp án A: \(2.\left( { – 1} \right) + 3.1 = 1 \ne 5\).
– Đáp án B: \(2.1 + 3.\left( { – 1} \right) = – 1 \ne 5\).
– Đáp án C: \(2.\left( { – 1} \right) + 3.\left( { – 1} \right) = – 5 \ne 5\).
– Đáp án D: \(2.1 + 3.1 = 5\).
Vậy cặp số \(\left( {1;1} \right)\) là một nghiệm của phương trình \(2x + 3y = 5\).
Chọn D.
Câu 4 – Đường kính và dây của đường tròn
Phương pháp:
Trong một đường tròn, đường kính là dây cung lớn nhất.
Cách giải:
Đường tròn \(\left( {O;4cm} \right)\) có đường kính bằng \(8cm\).
Vì trong một đường tròn, đường kính là dây cung lớn nhất nên dây lớn nhất của \(\left( {O;4cm} \right)\) bằng \(8cm\).
Chọn B.
Câu 5 – Một số hệ thức về cạnh và đường cao trong tam giác vuông
Phương pháp:
Sử dụng hệ thức lượng trong tam giác vuông.
Cách giải:
Xét tam giác \(MNP\) vuông tại \(M\), đường cao \(MH\) ta có: \(\dfrac{1}{{M{H^2}}} = \dfrac{1}{{M{N^2}}} + \dfrac{1}{{M{P^2}}}\).
Vậy khẳng định C đúng.
Chọn C.
Câu 6 – Vị trí tương đối của hai đường tròn
Phương pháp:
Hai đường tròn \(\left( {O;R} \right)\) và \(\left( {I;r} \right)\) tiếp xúc trong khi và chỉ khi \(OI = \left| {R – r} \right|\).
Cách giải:
Hai đường tròn \(\left( {O;R} \right)\) và \(\left( {I;r} \right)\) (với \(R > r\)) tiếp xúc trong với nhau thì ta có \(OI = \left| {R – r} \right| = R – r\) (do \(R > r\)).
Chọn A.
Câu 7 – Tỉ số lượng giác của góc nhọn
Phương pháp:
Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông: \(\sin = \dfrac{{doi}}{{huyen}}\).
Cách giải:
Ta có: \(\sin C = \dfrac{{AB}}{{BC}}\).
Chọn C.
Câu 8 – Hệ hai phương trình bậc nhất hai ẩn
Phương pháp:
Thay nghiệm \(\left( {x;y} \right) = \left( {1;1} \right)\) vào hệ phương trình và tìm \(m,\,\,n\).
Cách giải:
Vì \(\left( {x;y} \right) = \left( {1;1} \right)\) là nghiệm của hệ phương trình nên ta có: \(\left\{ \begin{array}{l}2.1 + m.1 = 3\\n.1 + 2.1 = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2 + m = 3\\n + 2 = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 1\\n = 3\end{array} \right.\).
Chọn B.
Câu 9 – Tứ giác nội tiếp
Phương pháp:
Sử dụng định lí:
– Tứ giác có tổng hai góc đối diện bằng \({180^0}\) là tứ giác nội tiếp.
– Tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện là tứ giác nội tiếp.
Cách giải:
– Hình 1: Ta có: \(\angle ABC = \angle ADC = {90^0}\) \( \Rightarrow \angle ABC + \angle ADC = {90^0} + {90^0} = {180^0}\).
\( \Rightarrow ABCD\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối diện bằng \({180^0}\)).
– Hình 2: Ta có: \(\angle QMN + \angle QPN = {70^0} + {110^0} = {180^0}\).
\( \Rightarrow MNPQ\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối diện bằng \({180^0}\)).
– Hình 3: Ta có: \(\angle GKI = \angle IHx\).
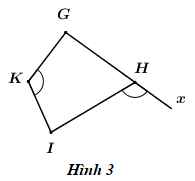
\( \Rightarrow GHIK\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối diện bằng \({180^0}\)).
– Hình 3: Ta có: \(\angle EFJ > {90^0},\,\,\angle ELJ = {90^0}\) \( \Rightarrow \angle EFJ + \angle ELJ > {180^0}\).
\( \Rightarrow EFJL\) không là tứ giác nội tiếp.
Vậy có 3 tứ giác nội tiếp.
Chọn A.
Câu 10 – Hàm số bậc nhất
Phương pháp:
Hàm số bậc nhất là hàm số có dạng \(y = ax + b\,\,\left( {a \ne 0} \right)\).
Cách giải:
Hàm số \(y = – 4x + 3\) là hàm số bậc nhất.
Chọn A.
Câu 11 – Phương trình bậc hai một ẩn số
Phương pháp:
Phương trình \(a{x^2} + bx + c = 0\,\,\left( {a \ne 0} \right)\) có hai nghiệm trái dấu \( \Leftrightarrow ac < 0\).
Cách giải:
Phương trình \({x^2} + 2\left( {m – 2} \right)x + m – 3 = 0\) có hai nghiệm trái dấu khi và chỉ khi \(1.\left( {m – 3} \right) < 0 \Leftrightarrow m < 3\).
Chọn D.
Câu 12 – Giải hệ phương trình bằng phương pháp cộng đại số
Phương pháp:
– Giải hệ phương trình bằng phương pháp cộng đại số.
– Xác định nghiệm của hệ phương trình, suy ra \({x_0},\,\,{y_0}\) và tính \(S = {x_0} + {y_0}\).
Cách giải:
Ta có:
\(\left\{ \begin{array}{l}x + 3y = – 7\\x + 2y = – 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = – 3\\x + 2y = – 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = – 3\\x + 2.\left( { – 3} \right) = – 4\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}y = – 3\\x – 6 = – 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = – 3\\x = 2\end{array} \right.\).
\( \Rightarrow \left( {2; – 3} \right)\) là nghiệm duy nhất của hệ phương trình đã cho.
\( \Rightarrow {x_0} = 2,\,\,{y_0} = – 3\).
Vậy \(S = {x_0} + {y_0} = 2 + \left( { – 3} \right) = – 1\).
Chọn B.
Câu 13 – Góc nội tiếp
Phương pháp:
Góc nội tiếp là góc của đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
Cách giải:
Ta thấy: \(\angle ABC\) là góc có đỉnh \(B\) nằm trên đường tròn, hai cạnh của góc chứa hai dây cung \(BA,\,\,BC\) của đường tròn. Do đó \(\angle ABC\) là góc nội tiếp của đường tròn \(\left( O \right)\).
Chọn A.
Câu 14 – Hệ thức Vi-ét và ứng dụng
Phương pháp:
Sử dụng định lí Vi-ét: Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\,\,\left( {a \ne 0} \right)\) có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) thì \({x_1} + {x_2} = – \dfrac{b}{a}\).
Cách giải:
Phương trình \({x^2} – 5x – 7 = 0\) có 2 nghiệm trái dấu (do \(ac = – 7 < 0\)).
Áp dụng định lí Vi-et ta có: Tổng hai nghiệm của phương trình bằng \(\dfrac{{ – b}}{a} = \dfrac{{ – \left( { – 5} \right)}}{1} = 5\).
Chọn B.
Câu 15 – Hình cầu – Diện tích mặt cầu và thể tích mặt cầu
Phương pháp:
Thể tích khối cầu bán kính \(r\) là \(V = \dfrac{4}{3}\pi {r^3}\).
Cách giải:
Thể tích khối cầu có bán kính \(r = 5\,\,cm\) là \(V = \dfrac{4}{3}\pi {.5^3} = \dfrac{{500\pi }}{3}\,\,\left( {c{m^3}} \right)\).
Chọn C.
Câu 16 – Hàm số bậc nhất
Phương pháp:
Cho hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\):
– Hàm số đồng biến trên \(\mathbb{R}\) khi \(a > 0\).
– Hàm số đồng biến trên \(\mathbb{R}\) khi \(a < 0\).
Cách giải:
Hàm số \(y = \left( {m + 2} \right)x – 5\) đồng biến trên \(\mathbb{R}\) khi và chỉ khi \(m + 2 > 0 \Leftrightarrow m > – 2\).
Chọn A.
Câu 17 – Góc có đỉnh ở bên trong đường tròn
Phương pháp:
Góc có đỉnh nằm bên trong đường tròn là góc có đỉnh nằm bên trong đường tròn, hai cạnh của góc chứa hai dây cung của đường tròn đó.
Cách giải:
Góc có đỉnh nằm bên trong đường tròn là hình 3.
Chọn D.
Câu 18 – Hình trụ – Diện tích xung quanh và thể tích của Hình trụ
Phương pháp:
Diện tích xung quanh của hình trụ có chiều cao \(h\), bán kính đáy \(r\) là \({S_{xq}} = 2\pi rh\).
Cách giải:
Diện tích xung quanh của hình trụ có chiều cao \(h\), bán kính đáy \(r\) là \({S_{xq}} = 2\pi rh\).
Chọn C.
Câu 19 – Hàm số y = ax^2 (a ≠ 0)
Phương pháp:
Thay \(x = 3\) vào hàm số để tính giá trị của hàm số tại \(x = 3\).
Cách giải:
Thay \(x = 3\) vào hàm số \(y = 2{x^2}\) ta có: \(y = {2.3^2} = 18\).
Vậy giá trị của hàm số \(y = 2{x^2}\) tại \(x = 3\) là \(18\).
Chọn C.
Câu 20 – Căn thức bậc hai và hằng đẳng thức √A^(2)=|A|
Phương pháp:
– Sử dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\).
– Phá trị tuyệt đối: \(\left| A \right| = \left[ \begin{array}{l}\,\,A\,\,\,khi\,\,A \ge 0\\ – A\,\,khi\,\,A < 0\end{array} \right.\).
Cách giải:
Ta có:
\(\begin{array}{l}\,\,\,\,\dfrac{1}{{a – b}}.\sqrt {{4^2}{{\left( {a – b} \right)}^2}} \\ = \dfrac{1}{{a – b}}.4\left| {a – b} \right|\\ = \dfrac{1}{{a – b}}.4\left( {a – b} \right)\,\,\,\left( {Do\,\,a > b \Rightarrow a – b > 0} \right)\\ = 4.\end{array}\)
Chọn B.
Câu 21 – Góc có đỉnh ở bên trong đường tròn
Phương pháp:
Sử dụng định lí: Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
Cách giải:
Vì \(\angle AED\) là góc có đỉnh ở bên ngoài đường tròn nên
\(\begin{array}{l}\angle AED = \dfrac{{sd\,cung\,AmD – sd\,cung\,CnB}}{2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{{{110}^0} – {{40}^0}}}{2} = \dfrac{{{{70}^0}}}{2} = {35^0}\end{array}\)
Chọn C.
Câu 22 – Hệ thức Vi-ét và ứng dụng
Phương pháp:
Cho phương trình bậc hai \(a{x^2} + bx + c = 0\,\,\left( {a \ne 0} \right)\) có hai nghiệm, áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = – \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\).
Cách giải:
Vì \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \({x^2} – 2x – 2 = 0\) nên ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ – \left( { – 2} \right)}}{1} = 2\\{x_1}{x_2} = \dfrac{{ – 2}}{1} = – 2\end{array} \right.\).
Vậy \(T = {x_1} + {x_2} + 2{x_1}{x_2} = 2 + 2.\left( { – 2} \right) = – 2\).
Chọn C.
Câu 23 – Góc nội tiếp
Phương pháp:
Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.
Cách giải:
Xét đường tròn \(\left( O \right)\) ta có: \(\angle DAC = \angle DBC = {80^0}\) (hai góc nội tiếp cùng chắn cung \(CD\))
Chọn D.
Câu 24 – Căn thức bậc hai và hằng đẳng thức √A^(2)=|A|
Phương pháp:
Biểu thức \(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0.\)
Cách giải:
Biểu thức \(\sqrt {x – 2} \) xác định \( \Leftrightarrow x – 2 \ge 0 \Leftrightarrow x \ge 2.\)
Chọn A.
Câu 25 – Hệ hai phương trình bậc nhất hai ẩn
Phương pháp:
Hệ phương trình \(\left\{ \begin{array}{l}{a_1}x + {b_1}y = {c_1}\\{a_2}x + {b_2}y = {c_2}\end{array} \right.\) có vô số nghiệm \( \Leftrightarrow \dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} = \dfrac{{{c_1}}}{{{c_2}}}.\)
Cách giải:
Xét đáp án C: \(\left\{ \begin{array}{l}3x – 2y = 5\\6x – 4y = 10\end{array} \right.\) ta có: \(\dfrac{3}{6} = \dfrac{{ – 2}}{{ – 4}} = \dfrac{5}{{10}} = \dfrac{1}{2}\)
\( \Rightarrow \) Hệ phương trình có vô số nghiệm.
Chọn C.
Câu 26 – Ôn tập chương 1: Căn bậc hai. Căn bậc ba
Phương pháp:
Giải phương trình: \(\sqrt {f\left( x \right)} = a\,\,\left( {a \ge 0} \right) \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \ge 0\\f\left( x \right) = {a^2}\end{array} \right..\)
Cách giải:
\(\sqrt {3 + \sqrt x } = 4 \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\3 + \sqrt x = 16\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\\sqrt x = 13\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x = 169\end{array} \right. \Leftrightarrow x = 169\)
Vậy \(x = 169.\)
Chọn C.
Câu 27 – Sự xác định đường tròn. Tính chất đối xứng của đường tròn
Phương pháp:
Có một và chỉ một đường tròn đi qua 3 điểm phân biệt không thẳng hàng.
Cách giải:
Có một và chỉ một đường tròn đi qua 3 điểm phân biệt không thẳng hàng.
Chọn B.
Câu 28 – Đồ thị hàm số y = ax^2 (a ≠ 0)
Phương pháp:
Thay tọa độ điểm \(M\) vào hàm số đã cho để tìm \(a.\)
Cách giải:
Thay tọa độ điểm \(M\left( { – 1;\,\,2} \right)\) vào hàm số \(y = a{x^2}\,\,\left( {a \ne 0} \right)\) ta được: \(2 = a.{\left( { – 1} \right)^2} \Leftrightarrow a = 2\,\,\left( {tm} \right).\)
Vậy \(a = 2.\)
Chọn B.
Câu 29 – Tỉ số lượng giác của góc nhọn
Phương pháp:
Sử dụng các công thức tỉ số lượng giác của góc nhọn trong tam giác vuông.
Cách giải:
Ta có các công thức: \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }};\) \(\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }};\) \(\tan \alpha .\cot \alpha = 1;\) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1.\)
Vậy chỉ có đáp án A sai.
Chọn A.
Câu 30 – Hình nón – Hình nón cụt – Diện tích xung quanh và thể tích của hình nón, hình nón cụt
Phương pháp:
Thể tích của hình nón có bán kính đáy \(R\) và chiều cao \(h\) là: \(V = \dfrac{1}{3}\pi {R^2}h.\)
Cách giải:
Thể tích của hình nón đã cho là: \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {.3^2}.5 = 15\pi \,\,c{m^3}.\)
Chọn C.
Câu 31 – Hàm số bậc nhất
Phương pháp:
Hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\) nghịch biến trên \(\mathbb{R}\) khi \(a < 0.\)
Cách giải:
Trong các đáp án, chỉ có hàm số \(y = – 3x + 5\) là hàm số nghịch biến trên \(\mathbb{R}.\)
Chọn B.
Câu 32 – Công thức nghiệm thu gọn
Phương pháp:
Phương trình \(a{x^2} + 2b’x + c = 0\,\,\,\left( {a \ne 0} \right)\) có: \(\Delta ‘ = b{‘^2} – ac.\)
Cách giải:
Phương trình \(3{x^2} – 2mx – 1 = 0\) có \(\Delta ‘ = b{‘^2} – ac = {m^2} + 3.\)
Chọn A.
Câu 33 – Phương trình bậc nhất hai ẩn
Phương pháp:
Phương trình bậc nhất hai ẩn có dạng: \(ax + by = c\,\,\,\left( {ab \ne 0} \right).\)
Cách giải:
Trong các đáp án, chỉ có phương trình \(2x – 5y = 3\) là phương trình bậc nhất hai ẩn.
Chọn A.
Câu 34 – Đường thẳng song song và đường thẳng cắt nhau
Phương pháp:
Hai đường thẳng \({d_1}:\,\,\,y = {a_1}x + {b_1}\) và \({d_2}:\,\,\,y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\)
Cách giải:
Đường thẳng song song với đường thẳng \(y = – 2x + 3\) có dạng: \(y = – 2x + b\,\,\,\,\left( {b \ne 3} \right).\)
\( \Rightarrow \) Chỉ có đáp án A: \(y = – 2x + 7\) thỏa mãn.
Chọn A.
Câu 35 – Căn thức bậc hai và hằng đẳng thức √A^(2)=|A|
Phương pháp:
Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ – A\sqrt B \,\,\,khi\,\,\,\,A < 0\end{array} \right.,\,\,\,B \ge 0.\)
Cách giải:
Ta có: \(A = 3\sqrt {80} – 2\sqrt {20} \) \( = 3\sqrt {{4^2}.5} – 2\sqrt {{2^2}.5} \)\( = 3.4\sqrt 5 – 2.2\sqrt 5 = 8\sqrt 5 \)
Chọn B.
Câu 36 – Bất đẳng thức
Phương pháp:
Áp dụng BĐT Cô-si với 3 số thực không âm \(a,\,\,b,\,\,c\): \(a + b + c \ge 3\sqrt[3]{{abc}}\). Dấu “=” xảy ra khi và chỉ khi \(a = b = c\)
Cách giải:
Ta có:
\(\begin{array}{l}S = 2{a^2} + {b^2} + \dfrac{4}{a} + \dfrac{{54}}{b}\\S = \left( {2{a^2} + \dfrac{2}{a} + \dfrac{2}{a}} \right) + \left( {{b^2} + \dfrac{{27}}{b} + \dfrac{{27}}{b}} \right)\end{array}\)
Áp dụng BĐT Cô-si ta có:
\(\begin{array}{l}2{a^2} + \dfrac{2}{a} + \dfrac{2}{a} \ge 3\sqrt[3]{{2{a^2}.\dfrac{2}{a}.\dfrac{2}{a}}} = 6\\{b^2} + \dfrac{{27}}{b} + \dfrac{{27}}{b} \ge 3\sqrt[3]{{{b^2}.\dfrac{{27}}{b}.\dfrac{{27}}{b}}} = 27\end{array}\)
Khi đó ta có \(S \ge 6 + 27 = 33\).
\( \Rightarrow {S_{\min }} = 33\). Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}2{a^2} = \dfrac{2}{a}\\{b^2} = \dfrac{{27}}{b}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^3} = 1\\{b^3} = 27\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 3\end{array} \right.\).
Vậy khi đó \(T = a + 2b = 1 + 2.3 = 7\).
Chọn A.
Câu 37 – Ôn tập chương 3: Hệ hai phương trình bậc nhất một ẩn
Phương pháp:
Giải hệ phương trình bằng phương pháp cộng đại số để tìm \(x,\,\,y.\)
Sau đó giải hệ bất phương trình \(\left\{ \begin{array}{l}x > 0\\y > 0\end{array} \right.\) để tìm \(m.\)
Cách giải:
Ta có: \(\left\{ \begin{array}{l}2x + y = 3m\\x – y = – 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 3m – 9\\y = x + 9\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = m – 3\\y = m – 3 + 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = m – 3\\y = m + 6\end{array} \right.\)
Hệ phương trình có nghiệm \(\left( {x;\,\,y} \right)\) thỏa mãn \(\left\{ \begin{array}{l}x > 0\\y > 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m – 3 > 0\\m + 6 > 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m > 3\\m > – 6\end{array} \right. \Leftrightarrow m > 3.\)
Chọn C.
Câu 38 – Tìm giá trị lớn nhất, giá trị nhỏ nhất
Phương pháp:
Biến đổi biểu thức trong dấu căn bậc hai để tìm GTNN của biểu thức.
Cách giải:
Ta có:
\(\begin{array}{l}y = 4 + \sqrt {3{x^2} – 6x + 7} \\\,\,\,\,\, = 4 + \sqrt {3\left( {{x^2} – 2x} \right) + 7} \\\,\,\,\,\, = 4 + \sqrt {3\left( {{x^2} – 2x + 1} \right) + 4} \\\,\,\,\,\,\, = 4 + \sqrt {3{{\left( {x – 1} \right)}^2} + 4} \end{array}\)
Vì \({\left( {x – 1} \right)^2} \ge 0\,\,\forall x \Rightarrow 3{\left( {x – 1} \right)^2} \ge 0\,\,\forall x\) \( \Rightarrow 3{\left( {x – 1} \right)^2} + 4 \ge 4\,\,\forall x\)\( \Rightarrow \sqrt {3{{\left( {x – 1} \right)}^2} + 4} \ge 2\,\,\forall x\)
\( \Rightarrow y = 4 + \sqrt {3{{\left( {x – 1} \right)}^2} + 4} \ge 4 + 2 = 6\)
Dấu “=” xảy ra \( \Leftrightarrow x – 1 = 0 \Leftrightarrow x = 1.\)
Vậy \(Min\,\,y = 6\) khi \(x = 1.\)
Chọn C.
Câu 39 – Hình cầu – Diện tích mặt cầu và thể tích mặt cầu
Phương pháp:
Diện tích đường tròn bán kính \(R\) là: \(S = \pi {R^2}.\)
Diện tích phần bồn cây tăng thêm là: \(S = \pi {R^2} – \pi {r^2}.\)
Cách giải:
Diện tích của bồn cây ban đầu là: \({S_1} = \pi {r^2} = \pi \,\,\left( {{m^2}} \right).\)
Bán kính của bồn cây sau khi mở rộng là: \(R = 1 + 0,6 = 1,6\,\,m.\)
Diện tích của bồn cây sau khi mở rộng là: \({S_2} = \pi {R^2} = \pi .1,{6^2}\,\,\left( {{m^2}} \right).\)
\( \Rightarrow \) Diện tích của phần bồn cây mở rộng thêm là: \(S = \pi .1,{6^2} – \pi = \left( {1,{6^2} – 1} \right).3,14 \approx 4,9\,\,{m^2}.\)
Chọn D.
Câu 40 – Ôn tập tổng hợp chương 2, 3, 4 – Đại số
Phương pháp:
– Cho lần lượt \(x = 0,\,\,y = 0\) tìm tọa độ giao điểm của đường thẳng với các trục \(Ox,\,\,Oy\).
– Sử dụng công thức \(A\left( {a;0} \right) \Rightarrow OA = \left| a \right|,\,\,B\left( {0;b} \right) \Rightarrow OB = \left| b \right|\).
– Tính diện tích tam giác vuông \(OAB:\,\,{S_{\Delta OAB}} = \dfrac{1}{2}OA.OB\).
Cách giải:
Gọi \(A = d \cap Ox\).
Cho \(y = 0 \Rightarrow 2x + 4 = 0 \Leftrightarrow x = – 2\).
\( \Rightarrow A\left( { – 2;0} \right) \Rightarrow OA = \left| { – 2} \right| = 2\).
Gọi \(B = d \cap Oy\).
Cho \(x = 0 \Rightarrow y = 2.0 + 4 = 4\).
Tam giác \(OAB\) vuông tại \(O\) nên \({S_{\Delta OAB}} = \dfrac{1}{2}OA.OB = \dfrac{1}{2}.2.4 = 4\).
Chọn C.
Câu 41 – Đồ thị của hàm số y = ax + b (a ≠ 0)
Phương pháp:
– Đưa hàm số về dạng phương trình bậc nhất ẩn \(m\): \(Am + B = 0\), tìm điều kiện để phương trình nghiệm đúng \(A = B = 0\), từ đó xác định điểm cố định \(M\) mà đường thẳng \(d\) đi qua.
– Sử dụng định lí đường vuông góc và đường xiên, chứng minh \(d\left( {O;d} \right) \le OM\). Dấu “=” xảy ra \( \Leftrightarrow OM \bot d\).
Cách giải:
Ta có:
\(\begin{array}{l}\,\,\,\,\,y = \left( {m – 1} \right)x + 4m\\ \Leftrightarrow mx – x + 4m – y = 0\\ \Leftrightarrow \left( {x – 4} \right)m – x – y = 0\end{array}\)
Phương trình trên đúng với mọi \(m\) khi và chỉ khi \(\left\{ \begin{array}{l}x – 4 = 0\\ – x – y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = – 4\end{array} \right.\).
\( \Rightarrow \) Đường thẳng \(\left( d \right)\) đi qua điểm \(M\left( {4; – 4} \right)\,\,\forall m\).
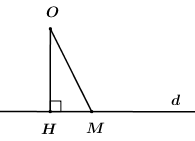
Gọi \(H\) là hình chiếu vuông góc của \(O\) lên đường thẳng \(d\), ta có \(d\left( {O;d} \right) = OH \le OM\) (quan hệ vuông góc giữa đường kính và dây cung).
Do đó khoảng cách từ \(O\) đến đường thẳng \(d\) đạt GTLN khi và chỉ khi
\(d\left( {O;d} \right) = OM = \sqrt {{{\left( {4 – 0} \right)}^2} + {{\left( { – 4 – 0} \right)}^2}} = 4\sqrt 2 \).
Chọn C.
Câu 42 – Giải bài toán bằng cách lập hệ phương trình
Phương pháp:
Gọi giá tiền thùng hàng A là \(x\) (nghìn đồng) (ĐK: \(x > 0\))
giá tiền thùng hàng B là \(y\) (nghìn đồng) (ĐK: \(y > 0\)).
– Tính giá tiền thùng hàng A sau khi tăng giá 20% và tiền thùng hàng B sau khi tăng giá 30%, dựa vào dữ kiện thùng A tăng giá 20% và thùng B tăng giá 30% thì người đó phải trả 302 nghìn đồng lập phương trình.
– Tương tự dựa vào dữ kiện thùng A giảm giá 10% và thùng B giảm giá 20% thì người đó phải trả 202 nghìn đồng để lập phương trình thứ hai.
– Suy ra hệ phương trình. Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số. Đối chiếu điều kiện và kết luận.
Cách giải:
Gọi giá tiền thùng hàng A là \(x\) (nghìn đồng) (ĐK: \(x > 0\))
giá tiền thùng hàng B là \(y\) (nghìn đồng) (ĐK: \(y > 0\)).
Giá tiền thùng hàng A sau khi tăng giá 20% là \(x + 20\% x = 1,2x\) (nghìn đồng).
Giá tiền thùng hàng B sau khi tăng giá 30% là \(y + 30\% y = 1,3y\) (nghìn đồng).
Vì thùng A tăng giá 20% và thùng B tăng giá 30% thì người đó phải trả 302 nghìn đồng nên ta có phương trình: \(1,2x + 1,3y = 302\).
Tương tự: khi thùng A giảm giá 10% và thùng B giảm giá 20% thì người đó phải trả 202 nghìn đồng nên ta có phương trình \(0,9x + 0,8y = 202\).
Khi đó ta có hệ phương trình:
\(\left\{ \begin{array}{l}1,2x + 1,3y = 302\\0,9x + 0,8y = 202\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}12x + 13y = 3020\\9x + 8y = 2020\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}36x + 39y = 9060\\36x + 32y = 8080\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}7y = 980\\9x + 8y = 2020\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}y = 140\,\,\,\left( {tm} \right)\\9x + 8.140 = 2020\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}y = 140\\x = 100\end{array} \right.\,\,\,\left( {tm} \right)\).
Vậy giá tiền thùng hàng A là 100 nghìn đồng, giá tiền thùng hàng B là 140 nghìn đồng.
Chọn B.
Câu 43 – Ôn tập chương 1: Căn bậc hai. Căn bậc ba
Phương pháp:
– Đánh giá, chặn khoảng giá trị của biểu thức A.
– Tìm các giá trị nguyên của A trong khoảng hoặc đoạn bị chặn, từ đó tìm \(x\) và đối chiếu điều kiện.
Cách giải:
Với \(x \ge 0\), ta có: \(A = \dfrac{{4\sqrt x + 16}}{{\sqrt x + 2}} = \dfrac{{4\left( {\sqrt x + 2} \right) + 8}}{{\sqrt x + 2}} = 4 + \dfrac{8}{{\sqrt x + 2}}\).
Vì \(\sqrt x + 2 \ge 2\) nên \(\dfrac{8}{{\sqrt x + 2}} \le 4\) \( \Rightarrow A = 4 + \dfrac{8}{{\sqrt x + 2}} \le 8\).
Lại có \(\dfrac{8}{{\sqrt x + 2}} > 0\) nên \(A = 4 + \dfrac{8}{{\sqrt x + 2}} > 4\).
\( \Rightarrow 4 < A \le 8\).
Mà \(A\) nhận giá trị nguyên \( \Rightarrow A \in \left\{ {5;6;7;8} \right\}\) \( \Rightarrow \dfrac{8}{{\sqrt x + 2}} \in \left\{ {1;2;3;4} \right\}\).
Ta có bảng sau:
|
\(\dfrac{8}{{\sqrt x + 2}}\)
|
1
|
2
|
3
|
4
|
|
\(\sqrt x + 2\)
|
8
|
4
|
\(\dfrac{8}{3}\)
|
2
|
|
\(\sqrt x \)
|
6
|
2
|
\(\dfrac{2}{3}\)
|
0
|
|
\(x\)
|
36
|
4
|
\(\dfrac{4}{9}\)
|
0
|
|
|
TM
|
TM
|
TM
|
TM
|
Vậy có 4 giá trị của \(x\) để biểu thức A nhận giá trị nguyên.
Chọn B.
Chú ý khi giải: Nhiều học sinh có cách giải sai lầm như sau:
Để \(A = 4 + \dfrac{8}{{\sqrt x + 2}} \in \mathbb{Z}\) thi \(\sqrt x + 2 \in \) Ư(8) \( = \left\{ { \pm 1; \pm 2; \pm 4; \pm 8} \right\}\).
Do \(\sqrt x + 2 \ge 2\) \( \Rightarrow \sqrt x + 2 \in \left\{ {2;4;8} \right\}\) \( \Rightarrow \sqrt x \in \left\{ {0;2;6} \right\} \Rightarrow x \in \left\{ {0;4;36} \right\}\).
Cách giải này sai do \(x\) không hẳn là số nguyên.
Câu 44 – Vị trí tương đối của hai đường tròn
Phương pháp:
– Tính độ dài \(CD\).
– Sử dụng định lí đường trung bình của hình thang, chứng minh \(E\) là trung điểm của \(HD\), từ đó tính độ dài \(HC\), từ đó áp dụng định lí Pytago tính \(O’H\).
– Chứng minh \(O’,\,\,H,\,\,F\) thẳng hàng, sử dụng quan hệ vuông góc giữa đường kính và dây cung và tiên đề Ơ-clit.
– Tính \(HF = O’F – O’H\).
Cách giải:
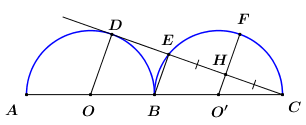
Vì \(CD\) là tiếp tuyến của \(\left( O \right)\) nên \(\angle ODC = {90^0}\) \( \Rightarrow \Delta OCD\) vuông tại \(D\).
Ta có \(OB = \dfrac{1}{2}AB = 9\) \( \Rightarrow OC = OB + BC = 9 + 18 = 27\).
Áp dụng định lí Pytago trong tam giác vuông \(OCD\) ta có:
\(\begin{array}{l}C{D^2} = O{C^2} – O{D^2}\\C{D^2} = {27^2} – {9^2}\\C{D^2} = 648\\ \Rightarrow CD = 18\sqrt 2 \end{array}\)
Vì \(AB = BC = 18 \Rightarrow OB = O’B = 9\)
\( \Rightarrow O\) là trung điểm của \(OO’\) (1).
Ta có: \(OD \bot CD\,\,\,\left( {cmt} \right)\)
\(O’H \bot EC \Rightarrow O’H \bot CD\) (quan hệ vuông góc giữa đường kính và dây cung).
\(BE \bot CE \Rightarrow BE \bot CD\) (\(\angle BEC = {90^0}\) do là góc nội tiếp chắn nửa đường tròn \(\left( {O’} \right)\)).
\( \Rightarrow OD\parallel O’H\parallel BE\,\,\left( 2 \right)\).
Từ (1) và (2) \( \Rightarrow E\) là trung điểm của \(HD\) (định lí đường trung bình của hình thang).
\( \Rightarrow DE = EH = CH\).
\( \Rightarrow CH = \frac{1}{3}CD = \frac{1}{3}.18\sqrt 2 = 6\sqrt 2 \).
Áp dụng định lí Pytago trong tam giác vuông \(O’HC\) có:
\(\begin{array}{l}O'{H^2} = O'{C^2} – H{C^2}\\O'{H^2} = {9^2} – {\left( {6\sqrt 2 } \right)^2}\\O'{H^2} = 9\\ \Rightarrow O’H = 3\end{array}\)
Vì \(F\) là điểm chính giữa của chung \(CE\) nên \(cungCF = cungEF \Rightarrow CF = EF\) (hai cung bằng nhau căng hai dây bằng nhau), do đó tam giác \(EFC\) cân tại \(F\), suy ra \(FH \bot CE\) (đường trung tuyến đồng thời là đường cao).
Lại có \(O’H \bot CE\,\,\left( {cmt} \right)\) \( \Rightarrow O’H \equiv FH\) (tiên đề Ơ-clit) hay \(O’,\,\,H,\,\,F\) thẳng hàng.
Vậy \(HF = O’F – O’H = 9 – 3 = 6\).
Chọn B.
Câu 45 (VDC) – Ôn tập chương 2: Đường tròn
Phương pháp:
– Đặt \(NP = 2x\) (ĐK: \(x > 0\)). Tính \(MI\) theo \(x\).
– Chứng minh \(O\) là trung điểm của \(MI\), tính \(OM,\,\,OI\) theo \(x\). Từ đó tính \(ON\) theo \(x\).
– Chứng minh \(\Delta ONI\) và \(\Delta PNK\) đồng dạng, từ đó tính \(NK\) theo \(x\).
– Chứng minh \(MI.NP = NK.MP\), giải phương trình tìm \(x\).
– Tính \(OK = NK – ON\).
Cách giải:
Đặt \(NP = 2x\) (ĐK: \(x > 0\)).
Vì \(\Delta MNP\) cân tại \(M\,\,\left( {gt} \right)\) nên \(I\) là trung điểm của \(NP\) (đường cao đồng thời là đường trung tuyến).
\( \Rightarrow NI = IP = x\).
Áp dụng định lí Pytago trong tam giác vuông \(MIP\) ta có: \(M{I^2} = M{P^2} – I{P^2} = 3 – {x^2}\) \( \Rightarrow MI = \sqrt {3 – {x^2}} \).
Ta có: \(MG = EI\,\,\left( {gt} \right),\,\,OG = OE\) (= bán kính của \(\left( O \right)\)) \( \Rightarrow OM = OI\).
\( \Rightarrow OM = OI = \frac{1}{2}MI = \frac{{\sqrt {3 – {x^2}} }}{2}\).
Áp dụng định lí Pytago trong tam giác vuông \(OIN\) có:
\(\begin{array}{l}O{N^2} = N{I^2} + O{I^2}\\O{N^2} = {x^2} + \frac{{3 – {x^2}}}{4} = \frac{{3{x^2} + 3}}{4}\\ \Rightarrow ON = \frac{{\sqrt 3 }}{2}.\sqrt {{x^2} + 1} \end{array}\)
Xét \(\Delta ONI\) và \(\Delta PNK\) có \(\angle KNP\) chung; \(\angle OIN = \angle PKN = {90^0}\).
\( \Rightarrow \Delta ONI \sim \Delta PNK\,\,\left( {g.g} \right)\)
\(\begin{array}{l} \Rightarrow \frac{{ON}}{{PN}} = \frac{{NI}}{{NK}}\\ \Rightarrow \frac{{\sqrt 3 .\sqrt {{x^2} + 1} }}{{2.2x}} = \frac{x}{{NK}}\\ \Rightarrow NK = \frac{{4{x^2}}}{{\sqrt 3 .\sqrt {{x^2} + 1} }}\end{array}\)
Ta có: \({S_{\Delta MNP}} = \frac{1}{2}MI.NP = \frac{1}{2}NK.MP\)
\(\begin{array}{l} \Rightarrow MI.NP = NK.MP\\ \Rightarrow \sqrt {3 – {x^2}} .2x = \frac{{4{x^2}}}{{\sqrt 3 .\sqrt {{x^2} + 1} }}.\sqrt 3 \\ \Leftrightarrow \sqrt {3 – {x^2}} .\sqrt {{x^2} + 1} = 2x\\ \Leftrightarrow \left( {3 – {x^2}} \right)\left( {{x^2} + 1} \right) = 4{x^2}\\ \Leftrightarrow – {x^4} + 2{x^2} + 3 = 4{x^2}\\ \Leftrightarrow {x^4} + 2{x^2} – 3 = 0\\ \Leftrightarrow {x^4} – {x^2} + 3{x^2} – 3 = 0\\ \Leftrightarrow {x^2}\left( {{x^2} – 1} \right) + 3\left( {{x^2} – 1} \right) = 0\\ \Leftrightarrow \left( {{x^2} – 1} \right)\left( {{x^2} + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} = 1\\{x^2} = 3\,\,\,\left( {Vo\,\,nghiem} \right)\end{array} \right.\\ \Leftrightarrow x = 1\,\,\left( {Do\,\,x > 0} \right)\end{array}\)
Với \(x = 1\) ta có \(NK = \frac{4}{{\sqrt 3 .\sqrt 2 }} = \frac{{2\sqrt 6 }}{3}\), \(ON = \frac{{\sqrt 3 }}{2}.\sqrt 2 = \frac{{\sqrt 6 }}{2}\).
Vậy \(OK = NK – ON = \frac{{2\sqrt 6 }}{3} – \frac{{\sqrt 6 }}{2} = \frac{{\sqrt 6 }}{6}\).
Chọn B.
Câu 46 (TH) – Một số hệ thức về cạnh và đường cao trong tam giác vuông
Phương pháp:
– Áp dụng định lý Pytago trong tam giác vuông \(AHB\) tính \(BH\).
– Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) tính \(BC\): \(A{B^2} = BH.BC\).
Cách giải:
Áp dụng định lý Pytago trong tam giác vuông \(AHB\) ta có:
\(\begin{array}{l}B{H^2} = A{B^2} – A{H^2}\\B{H^2} = {5^2} – {3^2}\\B{H^2} = 16\\ \Rightarrow BH = 4\,\,\left( {cm} \right)\end{array}\)
Áp dụng hệ thức lượng trong tam giác vuông \(ABC\), đường cao \(AH\) ta có:
\(A{B^2} = BH.BC\) \( \Rightarrow BC = \frac{{A{B^2}}}{{BH}} = \frac{{{5^2}}}{4} = \frac{{25}}{4}\,\,\left( {cm} \right)\).
Chọn C.
Câu 47 (VD) – Tỉ số lượng giác của góc nhọn
Phương pháp:
– Áp dụng định lý Pytago trong tam giác vuông \(AHB\) tính \(BH\).
– Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) tính \(BC\): \(A{B^2} = BH.BC\).
Cách giải:
Ta có hình vẽ như sau:
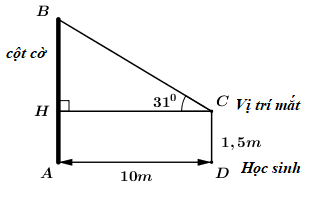
Theo bài ra ta có: \(AD = 10m,\,\,\,CD = 1,5m\), góc “nâng” \(\angle BCH = {31^0}\) (với \(H\) là hình chiếu vuông góc của \(C\) lên \(AB\)).
Vì \(ADCH\) là hình chữ nhật nên \(CH = AD = 10m\), \(AH = CD = 1,5m\).
Xét tam giác vuông \(BCH\) có: \(BH = CH.\tan {31^0} = 10.\tan {31^0}\,\,\left( m \right)\).
Vậy chiều cao cột cờ là \(AB = AH + BH = 1,5 + 10.tan{31^0} \approx 7,5\,\,\left( m \right)\).
Chọn C.
Câu 48 (VD) – Hệ số góc của đường thẳng y = ax + b (a ≠ 0)
Phương pháp:
– Tam giác \(OAB\) cân nên sẽ vuông cân tại \(O\).
– Sử dụng định nghĩa hệ số góc của đường thẳng \(y = ax + b\) là \(a = \tan \alpha \), với \(\alpha \) là góc tạo bởi đường thẳng và chiều dương của trục \(Ox\).
Cách giải:
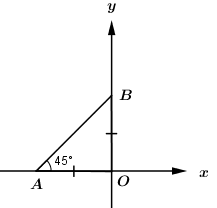 hoặc
hoặc 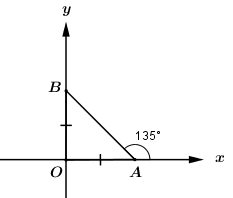
Tam giác \(OAB\) cân (gt), lại có \(\Delta OAB\) vuông tại \(O\), suy ra \(\Delta OAB\) vuông cân tại \(O\), do đó đường thẳng \(y = mx + 3\) tạo với chiều dương trục \(Ox\) hoặc góc \({45^0}\), hoặc góc \({135^0}\).
\( \Rightarrow \left[ \begin{array}{l}m = \tan {45^0}\\m = \tan {135^0}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = – 1\end{array} \right.\) \( \Rightarrow S = \left\{ { – 1;1} \right\}\).
Vậy tổng các phần tử của \(S\) là \( – 1 + 1 = 0\).
Chọn D.
Câu 49 (VDC) – Ôn tập tổng hợp chương 2, 3, 4 – Đại số
Phương pháp:
– Xét phương trình hoành độ giao điểm, tìm điều kiện để phương trình có 2 nghiệm phân biệt khác 0.
– Gọi \(A\left( {a;a + m – 1} \right),\,\,B\left( {b;b + m – 1} \right)\,\,\,\left( {a < 0,\,\,b > 0} \right)\). Tính \(\tan \angle AOM,\,\,\tan \angle BON\).
– Gọi \(M,\,\,N\) lần lượt là hình chiếu của \(A,\,\,B\) lên trục \(Ox\), chứng minh \(\angle AOM + \angle BON = {90^0}\) \( \Rightarrow \tan \angle AOM.\tan \angle BON = 1\).
– Áp dụng định lí Vi-ét. Sau đó giải phương trình tìm \(m\) và đối chiếu điều kiện.
Cách giải:
Xét phương trình hoành độ giao điểm \(\frac{1}{2}{x^2} = x + m – 1 \Leftrightarrow {x^2} – 2x – 2m + 2 = 0\,\,\left( * \right)\).
Để đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại 2 điểm phân biệt và ba điểm \(O,\,\,A,\,\,B\) tạo thành 1 tam giác thì phương trình (*) phải có 2 nghiệm phân biệt khác 0.
\( \Rightarrow \left\{ \begin{array}{l}\Delta ‘ > 0\\{0^2} – 2.0 – 2m + 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 + 2m – 2 > 0\\ – 2m + 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m – 1 > 0\\m \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > \frac{1}{2}\\m \ne 1\end{array} \right.\).
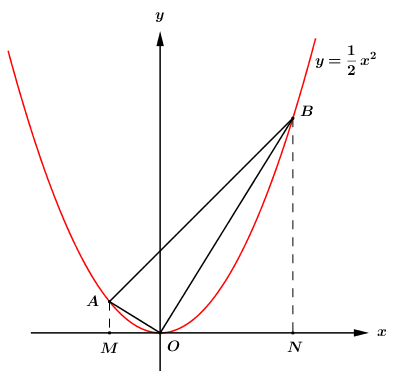
Gọi \(A\left( {a;a + m – 1} \right),\,\,B\left( {b;b + m – 1} \right)\,\,\,\left( {a < 0,\,\,b > 0} \right)\).
Gọi \(M,\,\,N\) là hình chiếu vuông góc của \(A,\,\,B\) lên trục \(Ox\). Khi đó ta có \(OM = \left| {} \right|\)
\(OM = \left| {{x_A}} \right| = – a,\,\,AM = \left| {{y_A}} \right| = a + m – 1\) (do \({y_A} = \frac{1}{2}x_A^2 \ge 0\)).
\(ON = \left| {{x_B}} \right| = b,\,\,BN = \left| {{y_B}} \right| = b + m – 1\) (do \({y_B} = \frac{1}{2}x_B^2 \ge 0\)).
Xét tam giác vuông \(OAM\) có: \(\tan \angle AOM = \frac{{AM}}{{OM}} = \frac{{a + m – 1}}{{ – a}}\).
Xét tam giác vuông \(OBM\) có: \(\tan \angle BON = \frac{{BN}}{{ON}} = \frac{{b + m – 1}}{b}\).
Vì \(\angle AOM + \angle BON = {90^0}\) nên \(\tan \angle AOM.\tan \angle BON = 1\).
\(\begin{array}{l} \Rightarrow \frac{{a + m – 1}}{{ – a}}.\frac{{b + m – 1}}{b} = 1\\ \Leftrightarrow ab + \left( {m – 1} \right)\left( {a + b} \right) + {\left( {m – 1} \right)^2} = – ab\\ \Leftrightarrow 2ab + \left( {m – 1} \right)\left( {a + b} \right) + {\left( {m – 1} \right)^2} = 0\,\,\,\,(**)\end{array}\)
Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}a + b = 2\\ab = – 2m + 2\end{array} \right.\).
Thay vào (**) ta có:
\(\begin{array}{l}2\left( { – 2m + 2} \right) + \left( {m – 1} \right).2 + {\left( {m – 1} \right)^2} = 0\\ \Leftrightarrow – 4m + 4 + 2m – 2 + {m^2} – 2m + 1 = 0\\ \Leftrightarrow {m^2} – 4m + 3 = 0\\ \Leftrightarrow {m^2} – m – 3m + 3 = 0\\ \Leftrightarrow m\left( {m – 1} \right) – 3\left( {m – 1} \right) = 0\\ \Leftrightarrow \left( {m – 1} \right)\left( {m – 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m – 1 = 0\\m – 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\,\,\,\,\left( {ktm} \right)\\m = 3\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy \(m = 3\).
Chọn A.
Chú ý khi giải: Các em học sinh cần lưu ý, để \(OAB\) là tam giác thì phương trình (*) cần có hai nghiệm phân biệt khác 0. Tránh chọn nhầm đáp án B do không loại nghiệm triệt để.
Câu 50 (VD) – Liên hệ giữa dây và khoảng cách từ tâm đến dây
Phương pháp:
Gọi \(H\) là hình chiếu của \(O\) trên \(CD\) \( \Rightarrow OH = 8cm\) và \(H\) là trung điểm của \(CD.\)
Áp dụng định lý Pitago cho \(\Delta OCH\) vuông tại \(H\) để tính \(AH \Rightarrow CD = 2AH.\)
Cách giải:
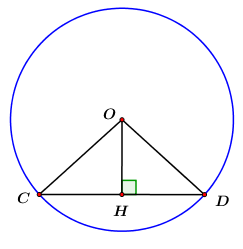
Gọi \(H\) là hình chiếu của \(O\) trên \(CD\) \( \Rightarrow OH = 8cm\) và \(H\) là trung điểm của \(CD.\)
Áp dụng định lý Pitago cho \(\Delta OCH\) vuông tại \(H\) ta có:
\(\begin{array}{l}CH = \sqrt {O{C^2} – O{H^2}} = \sqrt {{{10}^2} – {8^2}} = 6\,\,cm.\\ \Rightarrow CD = 2CH = 12\,\,cm.\end{array}\)
Chọn C.
 HỌC NGAY
Môn Toán học Lớp 12Đề thi, đề kiểm tra Toán lớp 12 SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SGK Toán lớp 12 SGK Toán 12 Nâng cao SBT Toán lớp 12 SBT Toán lớp 12 Nâng caoMôn Ngữ văn Lớp 12Luyện dạng đọc hiểu Đề thi, đề kiểm tra Ngữ Văn 12 mới Bài tập trắc nghiệm Văn 12 Soạn văn – Kết nối tri thức Soạn văn – Cánh diều Soạn văn – Chân trời sáng tạo Soạn văn 12 siêu ngắn Soạn văn 12 chi tiết Tác giả – Tác phẩm lớp 12 Xem thêmMôn Tiếng Anh Lớp 12Bài tập trắc nghiệm Tiếng Anh 12 Đề thi, đề kiểm tra Tiếng Anh 12 mới Tiếng Anh – Global Success Tiếng Anh – Friends Global Tiếng Anh – iLearn Smart World Tiếng Anh – Bright Tiếng Anh – English Discovery Bài tập trắc nghiệm Tiếng Anh 12 mới SGK Tiếng Anh 12 Mới Xem thêmMôn Vật lí Lớp 12Đề thi, kiểm tra Lí lớp 12 SGK Vật Lí – Kết nối tri thức SGK Vật Lí – Cánh diều SGK Vật Lí – Chân trời sáng tạo SGK Vật lí lớp 12 SGK Vật lí lớp 12 Nâng cao SBT Vật lí lớp 12 Bài tập trắc nghiệm Lí 12Môn Hóa học Lớp 12Đề thi, đề kiểm tra Hóa lớp 12 SGK Hóa – Kết nối tri thức SGK Hóa – Cánh diều SGK Hóa – Chân trời sáng tạo SGK Hóa lớp 12 SGK Hóa học lớp 12 Nâng cao SBT Hóa lớp 12 Bài tập trắc nghiệm Hóa 12Môn Sinh học Lớp 12Đề thi, đề kiểm tra Sinh lớp 12 SGK Sinh – Kết nối tri thức SGK Sinh – Cánh diều SGK Sinh – Chân trời sáng tạo SGK Sinh lớp 12 SGK Sinh lớp 12 Nâng cao SBT Sinh lớp 12 Bài tập trắc nghiệm Sinh 12Môn Lịch sử Lớp 12Tập bản đồ Lịch sử lớp 12 Đề thi, đề kiểm tra Lịch sử 12 SGK Lịch sử lớp 12 SBT Lịch sử lớp 12Môn Địa lí Lớp 12SGK Địa lí lớp 12 SBT Địa lí lớp 12 Tập bản đồ Địa lí lớp 12 Đề thi, kiểm tra Địa lí lớp 12Môn GDCD Lớp 12SGK GDCDMôn Công nghệ Lớp 12SGK Công nghệ 12Môn Tin học Lớp 12SGK Tin học lớp 12
HỌC NGAY
Môn Toán học Lớp 12Đề thi, đề kiểm tra Toán lớp 12 SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SGK Toán lớp 12 SGK Toán 12 Nâng cao SBT Toán lớp 12 SBT Toán lớp 12 Nâng caoMôn Ngữ văn Lớp 12Luyện dạng đọc hiểu Đề thi, đề kiểm tra Ngữ Văn 12 mới Bài tập trắc nghiệm Văn 12 Soạn văn – Kết nối tri thức Soạn văn – Cánh diều Soạn văn – Chân trời sáng tạo Soạn văn 12 siêu ngắn Soạn văn 12 chi tiết Tác giả – Tác phẩm lớp 12 Xem thêmMôn Tiếng Anh Lớp 12Bài tập trắc nghiệm Tiếng Anh 12 Đề thi, đề kiểm tra Tiếng Anh 12 mới Tiếng Anh – Global Success Tiếng Anh – Friends Global Tiếng Anh – iLearn Smart World Tiếng Anh – Bright Tiếng Anh – English Discovery Bài tập trắc nghiệm Tiếng Anh 12 mới SGK Tiếng Anh 12 Mới Xem thêmMôn Vật lí Lớp 12Đề thi, kiểm tra Lí lớp 12 SGK Vật Lí – Kết nối tri thức SGK Vật Lí – Cánh diều SGK Vật Lí – Chân trời sáng tạo SGK Vật lí lớp 12 SGK Vật lí lớp 12 Nâng cao SBT Vật lí lớp 12 Bài tập trắc nghiệm Lí 12Môn Hóa học Lớp 12Đề thi, đề kiểm tra Hóa lớp 12 SGK Hóa – Kết nối tri thức SGK Hóa – Cánh diều SGK Hóa – Chân trời sáng tạo SGK Hóa lớp 12 SGK Hóa học lớp 12 Nâng cao SBT Hóa lớp 12 Bài tập trắc nghiệm Hóa 12Môn Sinh học Lớp 12Đề thi, đề kiểm tra Sinh lớp 12 SGK Sinh – Kết nối tri thức SGK Sinh – Cánh diều SGK Sinh – Chân trời sáng tạo SGK Sinh lớp 12 SGK Sinh lớp 12 Nâng cao SBT Sinh lớp 12 Bài tập trắc nghiệm Sinh 12Môn Lịch sử Lớp 12Tập bản đồ Lịch sử lớp 12 Đề thi, đề kiểm tra Lịch sử 12 SGK Lịch sử lớp 12 SBT Lịch sử lớp 12Môn Địa lí Lớp 12SGK Địa lí lớp 12 SBT Địa lí lớp 12 Tập bản đồ Địa lí lớp 12 Đề thi, kiểm tra Địa lí lớp 12Môn GDCD Lớp 12SGK GDCDMôn Công nghệ Lớp 12SGK Công nghệ 12Môn Tin học Lớp 12SGK Tin học lớp 12 HỌC NGAY
Môn Toán học Lớp 11Chuyên đề học tập Toán – Kết nối tri thức Chuyên đề học tập Toán – Cánh diều Chuyên đề học tập Toán – Chân trời sáng tạo SBT Toán – Kết nối tri thức SBT Toán – Cánh diều SBT Toán – Chân trời sáng tạo SGK Toán 11 Nâng cao Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Xem thêmMôn Ngữ văn Lớp 11Đề thi, đề kiểm tra Văn – Kết nối tri thức Đề thi, đề kiểm tra Văn – Cánh diều Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Tóm tắt, bố cục Văn – Kết nối tri thức Tóm tắt, bố cục Văn – Cánh diều Tóm tắt, bố cục Văn – Chân trời sáng tạo Văn mẫu – Kết nối tri thức Văn mẫu – Cánh diều Văn mẫu – Chân trời sáng tạo Xem thêmMôn Tiếng Anh Lớp 11Lý thuyết Tiếng Anh 11 Bài tập trắc nghiệm Tiếng Anh – Friends Global Bài tập trắc nghiệm Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Global Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Bright Đề thi, đề kiểm tra Tiếng Anh – English Discovery SBT Tiếng Anh lớp 11 mới Xem thêmMôn Vật lí Lớp 11Chuyên đề học tập Lí – Cánh diều Chuyên đề học tập Lí – Chân trời sáng tạo SBT Vật lí – Kết nối tri thức SBT Vật lí – Cánh diều SBT Vật lí – Chân trời sáng tạo Lý thuyết Vật lí 11 Đề thi, đề kiểm tra Vật lí – Kết nối tri thức Đề thi, đề kiểm tra Vật lí – Cánh diều Đề thi, đề kiểm tra Vật lí – Chân trời sáng tạo Xem thêmMôn Hóa học Lớp 11SBT Hóa – Chân trời sáng tạo Lý thuyết Hóa 11 Đề thi, kiểm tra Hóa – Kết nối tri thức Đề thi, kiểm tra Hóa – Cánh diều Đề thi, kiểm tra Hóa – Chân trời sáng tạo Bài tập trắc nghiệm Hóa – Kết nối tri thức Bài tập trắc nghiệm Hóa – Cánh diều Bài tập trắc nghiệm Hóa – Chân trời sáng tạo Chuyên đề học tập Hóa – Cánh diều Xem thêmMôn Sinh học Lớp 11Chuyên đề học tập Sinh – Cánh diều Chuyên đề học tập Sinh – Chân trời sáng tạo SBT Sinh – Kết nối tri thức SBT Sinh – Cánh diều SBT Sinh – Chân trời sáng tạo Lý thuyết Sinh học 11 Đề thi, kiểm tra Sinh – Kết nối tri thức Đề thi, kiểm tra Sinh – Chân trời sáng tạo Đề thi, kiểm tra Sinh – Cánh diều Xem thêmMôn Lịch sử Lớp 11SGK Lịch sử – Kết nối tri thức SGK Lịch sử – Chân trời sáng tạo SGK Lịch sử – Cánh diều Đề thi, kiểm tra Lịch sử lớp 11Môn Địa lí Lớp 11SGK Địa lí – Kết nối tri thức SGK Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Địa lí lớp 11 SGK Địa lí – Cánh diềuMôn GD kinh tế và pháp luật Lớp 11SGK Giáo dục kinh tế và pháp luật – Kết nối tri thức SGK Giáo dục kinh tế và pháp luật – Chân trời sáng tạo SGK Giáo dục kinh tế và pháp luật – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 11SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 11SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diềuMôn GD Quốc phòng và An ninh Lớp 11SGK Giáo dục quốc phòng và an ninh – Kết nối tri thức SGK Giáo dục quốc phòng và an ninh – Cánh diều
HỌC NGAY
Môn Toán học Lớp 11Chuyên đề học tập Toán – Kết nối tri thức Chuyên đề học tập Toán – Cánh diều Chuyên đề học tập Toán – Chân trời sáng tạo SBT Toán – Kết nối tri thức SBT Toán – Cánh diều SBT Toán – Chân trời sáng tạo SGK Toán 11 Nâng cao Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Xem thêmMôn Ngữ văn Lớp 11Đề thi, đề kiểm tra Văn – Kết nối tri thức Đề thi, đề kiểm tra Văn – Cánh diều Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Tóm tắt, bố cục Văn – Kết nối tri thức Tóm tắt, bố cục Văn – Cánh diều Tóm tắt, bố cục Văn – Chân trời sáng tạo Văn mẫu – Kết nối tri thức Văn mẫu – Cánh diều Văn mẫu – Chân trời sáng tạo Xem thêmMôn Tiếng Anh Lớp 11Lý thuyết Tiếng Anh 11 Bài tập trắc nghiệm Tiếng Anh – Friends Global Bài tập trắc nghiệm Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Global Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Bright Đề thi, đề kiểm tra Tiếng Anh – English Discovery SBT Tiếng Anh lớp 11 mới Xem thêmMôn Vật lí Lớp 11Chuyên đề học tập Lí – Cánh diều Chuyên đề học tập Lí – Chân trời sáng tạo SBT Vật lí – Kết nối tri thức SBT Vật lí – Cánh diều SBT Vật lí – Chân trời sáng tạo Lý thuyết Vật lí 11 Đề thi, đề kiểm tra Vật lí – Kết nối tri thức Đề thi, đề kiểm tra Vật lí – Cánh diều Đề thi, đề kiểm tra Vật lí – Chân trời sáng tạo Xem thêmMôn Hóa học Lớp 11SBT Hóa – Chân trời sáng tạo Lý thuyết Hóa 11 Đề thi, kiểm tra Hóa – Kết nối tri thức Đề thi, kiểm tra Hóa – Cánh diều Đề thi, kiểm tra Hóa – Chân trời sáng tạo Bài tập trắc nghiệm Hóa – Kết nối tri thức Bài tập trắc nghiệm Hóa – Cánh diều Bài tập trắc nghiệm Hóa – Chân trời sáng tạo Chuyên đề học tập Hóa – Cánh diều Xem thêmMôn Sinh học Lớp 11Chuyên đề học tập Sinh – Cánh diều Chuyên đề học tập Sinh – Chân trời sáng tạo SBT Sinh – Kết nối tri thức SBT Sinh – Cánh diều SBT Sinh – Chân trời sáng tạo Lý thuyết Sinh học 11 Đề thi, kiểm tra Sinh – Kết nối tri thức Đề thi, kiểm tra Sinh – Chân trời sáng tạo Đề thi, kiểm tra Sinh – Cánh diều Xem thêmMôn Lịch sử Lớp 11SGK Lịch sử – Kết nối tri thức SGK Lịch sử – Chân trời sáng tạo SGK Lịch sử – Cánh diều Đề thi, kiểm tra Lịch sử lớp 11Môn Địa lí Lớp 11SGK Địa lí – Kết nối tri thức SGK Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Địa lí lớp 11 SGK Địa lí – Cánh diềuMôn GD kinh tế và pháp luật Lớp 11SGK Giáo dục kinh tế và pháp luật – Kết nối tri thức SGK Giáo dục kinh tế và pháp luật – Chân trời sáng tạo SGK Giáo dục kinh tế và pháp luật – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 11SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 11SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diềuMôn GD Quốc phòng và An ninh Lớp 11SGK Giáo dục quốc phòng và an ninh – Kết nối tri thức SGK Giáo dục quốc phòng và an ninh – Cánh diều HỌC NGAY
Môn Toán học Lớp 10SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Chuyên đề học tập Toán – Kết nối tri thức Chuyên đề học tập Toán – Chân trời sáng tạo Chuyên đề học tập Toán – Cánh diều Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Lý thuyết Toán 10 Xem thêmMôn Ngữ văn Lớp 10Soạn văn – Cánh Diều – siêu ngắn Bài tập trắc nghiệm Văn – Kết nối tri thức Soạn văn – Cánh Diều – chi tiết Bài tập trắc nghiệm Văn – Cánh diều Tác giả tác phẩm lớp 10 Bài tập trắc nghiệm Văn – Chân trời sáng tạo Văn mẫu – Kết nối tri thức Văn mẫu – Chân trời sáng tạo Văn mẫu – Cánh diều Xem thêmMôn Tiếng Anh Lớp 10Tiếng Anh – Bright Tiếng Anh – Explore New Worlds SBT Global Success SBT Friends Global SBT iLearn Smart World SBT Bright SBT English Discovery Bài tập trắc nghiệm Tiếng Anh – Global Success Bài tập trắc nghiệm Tiếng Anh – Friends Global Xem thêmMôn Vật lí Lớp 10SBT Vật lí – Chân trời sáng tạo SBT Vật lí – Cánh diều Bài tập trắc nghiệm Lí – Kết nối tri thức Bài tập trắc nghiệm Lí – Chân trời sáng tạo Bài tập trắc nghiệm Lí – Cánh diều Đề thi, đề kiểm tra Vật lí – Chân trời sáng tạo Đề thi, đề kiểm tra Vật lí – Kết nối tri thức Đề thi, đề kiểm tra Vật lí – Cánh diều Chuyên đề học tập Lí – Kết nối tri thức Xem thêmMôn Hóa học Lớp 10SBT Hóa – Chân trời sáng tạo SBT Hóa 10 – Cánh diều Chuyên đề học tập Hóa – Kết nối tri thức Chuyên đề học tập Hóa 10 – Chân trời sáng tạo Chuyên đề học tập Hóa 10 – Cánh diều Bài tập trắc nghiệm Hóa – Kết nối tri thức Bài tập trắc nghiệm Hóa – Chân trời sáng tạo Bài tập trắc nghiệm Hóa – Cánh diều Đề thi, kiểm tra Hóa – Kết nối tri thức Xem thêmMôn Sinh học Lớp 10SBT Sinh – Chân trời sáng tạo SBT Sinh – Cánh diều Chuyên đề học tập Sinh – Kết nối tri thức Chuyên đề học tập Sinh – Chân trời sáng tạo Bài tập trắc nghiệm Sinh – Kết nối tri thức Bài tập trắc nghiệm Sinh – Chân trời sáng tạo Bài tập trắc nghiệm Sinh – Cánh diều Đề thi, kiểm tra Sinh – Kết nối tri thức Đề thi, kiểm tra Sinh – Chân trời sáng tạo Xem thêmMôn Lịch sử Lớp 10SBT Lịch sử – Chân trời sáng tạo SBT Lịch sử – Cánh Diều Chuyên đề học tập Lịch sử – Kết nối tri thức Đề thi, đề kiểm tra Lịch sử – Kết nối tri thức Đề thi, đề kiểm tra Lịch sử lớp 10 – Chân trời sáng tạo Đề thi, đề kiểm tra Lịch sử – Cánh diều SGK Lịch sử – Kết nối tri thức SGK Lịch sử – Chân trời sáng tạo SGK Lịch sử – Cánh Diều Xem thêmMôn Địa lí Lớp 10SBT Địa lí – Chân trời sáng tạo Đề thi, đề kiểm tra Địa lí – Kết nối tri thức Đề thi, đề kiểm tra Địa lí lớp 10 – Chân trời sáng tạo Đề thi, đề kiểm tra Địa lí – Kết nối tri thức SGK Địa lí – Kết nối tri thức SGK Địa lí – Cánh Diều SGK Địa lí – Chân trời sáng tạo SBT Địa lí – Kết nối tri thứcMôn GDCD Lớp 10SGK Giáo dục kinh tế và pháp luật – KNTT SGK Giáo dục kinh tế và pháp luật – CTST SGK Giáo dục kinh tế và pháp luật – Cánh diềuMôn Tin học Lớp 10SGK Tin học – Kết nối tri thức SGK Tin học – Cánh Diều SBT Tin học – Kết nối tri thứcMôn HĐ trải nghiệm, hướng nghiệp Lớp 10SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh DiềuMôn Giáo dục thể chất Lớp 10SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diềuMôn GD Quốc phòng và An ninh Lớp 10SGK Giáo dục quốc phòng và an ninh – Kết nối tri thức SGK Giáo dục quốc phòng và an ninh – Cánh diều
HỌC NGAY
Môn Toán học Lớp 10SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Chuyên đề học tập Toán – Kết nối tri thức Chuyên đề học tập Toán – Chân trời sáng tạo Chuyên đề học tập Toán – Cánh diều Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Lý thuyết Toán 10 Xem thêmMôn Ngữ văn Lớp 10Soạn văn – Cánh Diều – siêu ngắn Bài tập trắc nghiệm Văn – Kết nối tri thức Soạn văn – Cánh Diều – chi tiết Bài tập trắc nghiệm Văn – Cánh diều Tác giả tác phẩm lớp 10 Bài tập trắc nghiệm Văn – Chân trời sáng tạo Văn mẫu – Kết nối tri thức Văn mẫu – Chân trời sáng tạo Văn mẫu – Cánh diều Xem thêmMôn Tiếng Anh Lớp 10Tiếng Anh – Bright Tiếng Anh – Explore New Worlds SBT Global Success SBT Friends Global SBT iLearn Smart World SBT Bright SBT English Discovery Bài tập trắc nghiệm Tiếng Anh – Global Success Bài tập trắc nghiệm Tiếng Anh – Friends Global Xem thêmMôn Vật lí Lớp 10SBT Vật lí – Chân trời sáng tạo SBT Vật lí – Cánh diều Bài tập trắc nghiệm Lí – Kết nối tri thức Bài tập trắc nghiệm Lí – Chân trời sáng tạo Bài tập trắc nghiệm Lí – Cánh diều Đề thi, đề kiểm tra Vật lí – Chân trời sáng tạo Đề thi, đề kiểm tra Vật lí – Kết nối tri thức Đề thi, đề kiểm tra Vật lí – Cánh diều Chuyên đề học tập Lí – Kết nối tri thức Xem thêmMôn Hóa học Lớp 10SBT Hóa – Chân trời sáng tạo SBT Hóa 10 – Cánh diều Chuyên đề học tập Hóa – Kết nối tri thức Chuyên đề học tập Hóa 10 – Chân trời sáng tạo Chuyên đề học tập Hóa 10 – Cánh diều Bài tập trắc nghiệm Hóa – Kết nối tri thức Bài tập trắc nghiệm Hóa – Chân trời sáng tạo Bài tập trắc nghiệm Hóa – Cánh diều Đề thi, kiểm tra Hóa – Kết nối tri thức Xem thêmMôn Sinh học Lớp 10SBT Sinh – Chân trời sáng tạo SBT Sinh – Cánh diều Chuyên đề học tập Sinh – Kết nối tri thức Chuyên đề học tập Sinh – Chân trời sáng tạo Bài tập trắc nghiệm Sinh – Kết nối tri thức Bài tập trắc nghiệm Sinh – Chân trời sáng tạo Bài tập trắc nghiệm Sinh – Cánh diều Đề thi, kiểm tra Sinh – Kết nối tri thức Đề thi, kiểm tra Sinh – Chân trời sáng tạo Xem thêmMôn Lịch sử Lớp 10SBT Lịch sử – Chân trời sáng tạo SBT Lịch sử – Cánh Diều Chuyên đề học tập Lịch sử – Kết nối tri thức Đề thi, đề kiểm tra Lịch sử – Kết nối tri thức Đề thi, đề kiểm tra Lịch sử lớp 10 – Chân trời sáng tạo Đề thi, đề kiểm tra Lịch sử – Cánh diều SGK Lịch sử – Kết nối tri thức SGK Lịch sử – Chân trời sáng tạo SGK Lịch sử – Cánh Diều Xem thêmMôn Địa lí Lớp 10SBT Địa lí – Chân trời sáng tạo Đề thi, đề kiểm tra Địa lí – Kết nối tri thức Đề thi, đề kiểm tra Địa lí lớp 10 – Chân trời sáng tạo Đề thi, đề kiểm tra Địa lí – Kết nối tri thức SGK Địa lí – Kết nối tri thức SGK Địa lí – Cánh Diều SGK Địa lí – Chân trời sáng tạo SBT Địa lí – Kết nối tri thứcMôn GDCD Lớp 10SGK Giáo dục kinh tế và pháp luật – KNTT SGK Giáo dục kinh tế và pháp luật – CTST SGK Giáo dục kinh tế và pháp luật – Cánh diềuMôn Tin học Lớp 10SGK Tin học – Kết nối tri thức SGK Tin học – Cánh Diều SBT Tin học – Kết nối tri thứcMôn HĐ trải nghiệm, hướng nghiệp Lớp 10SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh DiềuMôn Giáo dục thể chất Lớp 10SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diềuMôn GD Quốc phòng và An ninh Lớp 10SGK Giáo dục quốc phòng và an ninh – Kết nối tri thức SGK Giáo dục quốc phòng và an ninh – Cánh diều HỌC NGAY
Môn Toán học Lớp 9Tài liệu Dạy – học Toán 9 Đề thi, đề kiểm tra Toán lớp 9 Đề thi vào 10 môn Toán SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SGK Toán 9 – Cùng khám phá SGK Toán lớp 9 SBT Toán lớp 9 Xem thêmMôn Ngữ văn Lớp 9Vở bài tập Ngữ văn lớp 9 Bài tập trắc nghiệm Văn 9 Đề thi vào 10 môn Văn Đề thi, đề kiểm tra Văn 9 Soạn văn – Kết nối tri thức Soạn văn – Cánh diều Soạn văn – Chân trời sáng tạo Soạn văn 9 siêu ngắn Soạn văn 9 chi tiết Xem thêmMôn Tiếng Anh Lớp 9Tiếng Anh – Friends Plus Tiếng Anh – iLearn Smart World Tiếng Anh – Right on! Tiếng Anh – English Discovery Bài tập trắc nghiệm Tiếng Anh 9 mới Đề thi vào 10 môn Anh Đề thi, đề kiểm tra Tiếng Anh 9 mới Tiếng Anh – Global Success SGK Tiếng Anh lớp 9 Mới Xem thêmMôn Vật lí Lớp 9Tài liệu Dạy – Học Vật lí 9 Đề thi, kiểm tra Lí lớp 9 SGK Vật lí lớp 9 SBT Vật lí lớp 9 Vở bài tập Vật lí 9 Bài tập trắc nghiệm Lí 9Môn Hóa học Lớp 9Tài liệu Dạy – học Hóa học 9 Đề thi, đề kiểm tra Hóa lớp 9 SGK Hóa lớp 9 SBT Hóa lớp 9 Vở bài tập Hoá học 9 Bài tập trắc nghiệm Hóa 9Môn Sinh học Lớp 9Bài tập trắc nghiệm Sinh 9 Đề thi, đề kiểm tra Sinh lớp 9 SGK Sinh lớp 9 SBT Sinh lớp 9 Vở bài tập Sinh học 9 Đề thi, đề kiểm tra Sinh lớp 9Môn Lịch sử Lớp 9Đề thi, kiểm tra Lịch sử lớp 9 SGK Lịch sử lớp 9 VBT Lịch sử lớp 9 Tập bản đồ Lịch sử lớp 9 SBT Lịch sử lớp 9Môn Địa lí Lớp 9Đề thi, kiểm tra Địa lí lớp 9 SGK Địa lí lớp 9 SBT Địa lí lớp 9 VBT Địa lí lớp 9 Tập bản đồ Địa lí lớp 9Môn Công nghệ Lớp 9SGK Công nghệ 9Môn Tin học Lớp 9SGK Tin học lớp 9Môn Khoa học tự nhiên Lớp 9SGK Khoa học tự nhiên – Cánh diều SGK Khoa học tự nhiên – Chân trời sáng tạo SGK Khoa học tự nhiên – Kết nối tri thứcMôn Âm nhạc và mỹ thuật Lớp 9Âm nhạc và mỹ thuật lớp 9
HỌC NGAY
Môn Toán học Lớp 9Tài liệu Dạy – học Toán 9 Đề thi, đề kiểm tra Toán lớp 9 Đề thi vào 10 môn Toán SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SGK Toán 9 – Cùng khám phá SGK Toán lớp 9 SBT Toán lớp 9 Xem thêmMôn Ngữ văn Lớp 9Vở bài tập Ngữ văn lớp 9 Bài tập trắc nghiệm Văn 9 Đề thi vào 10 môn Văn Đề thi, đề kiểm tra Văn 9 Soạn văn – Kết nối tri thức Soạn văn – Cánh diều Soạn văn – Chân trời sáng tạo Soạn văn 9 siêu ngắn Soạn văn 9 chi tiết Xem thêmMôn Tiếng Anh Lớp 9Tiếng Anh – Friends Plus Tiếng Anh – iLearn Smart World Tiếng Anh – Right on! Tiếng Anh – English Discovery Bài tập trắc nghiệm Tiếng Anh 9 mới Đề thi vào 10 môn Anh Đề thi, đề kiểm tra Tiếng Anh 9 mới Tiếng Anh – Global Success SGK Tiếng Anh lớp 9 Mới Xem thêmMôn Vật lí Lớp 9Tài liệu Dạy – Học Vật lí 9 Đề thi, kiểm tra Lí lớp 9 SGK Vật lí lớp 9 SBT Vật lí lớp 9 Vở bài tập Vật lí 9 Bài tập trắc nghiệm Lí 9Môn Hóa học Lớp 9Tài liệu Dạy – học Hóa học 9 Đề thi, đề kiểm tra Hóa lớp 9 SGK Hóa lớp 9 SBT Hóa lớp 9 Vở bài tập Hoá học 9 Bài tập trắc nghiệm Hóa 9Môn Sinh học Lớp 9Bài tập trắc nghiệm Sinh 9 Đề thi, đề kiểm tra Sinh lớp 9 SGK Sinh lớp 9 SBT Sinh lớp 9 Vở bài tập Sinh học 9 Đề thi, đề kiểm tra Sinh lớp 9Môn Lịch sử Lớp 9Đề thi, kiểm tra Lịch sử lớp 9 SGK Lịch sử lớp 9 VBT Lịch sử lớp 9 Tập bản đồ Lịch sử lớp 9 SBT Lịch sử lớp 9Môn Địa lí Lớp 9Đề thi, kiểm tra Địa lí lớp 9 SGK Địa lí lớp 9 SBT Địa lí lớp 9 VBT Địa lí lớp 9 Tập bản đồ Địa lí lớp 9Môn Công nghệ Lớp 9SGK Công nghệ 9Môn Tin học Lớp 9SGK Tin học lớp 9Môn Khoa học tự nhiên Lớp 9SGK Khoa học tự nhiên – Cánh diều SGK Khoa học tự nhiên – Chân trời sáng tạo SGK Khoa học tự nhiên – Kết nối tri thứcMôn Âm nhạc và mỹ thuật Lớp 9Âm nhạc và mỹ thuật lớp 9 HỌC NGAY
Môn Toán học Lớp 8SBT Toán – Kết nối tri thức SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Vở thực hành Toán Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Lý thuyết Toán 8 Bài tập trắc nghiệm Toán – Kết nối tri thức Xem thêmMôn Ngữ văn Lớp 8Soạn văn chi tiết – Cánh diều Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Soạn văn siêu ngắn – Cánh diều Tóm tắt, bố cục Văn – Kết nối tri thức SBT Văn – Kết nối tri thức Tóm tắt, bố cục Văn – Cánh diều SBT Văn – Chân trời sáng tạo Tóm tắt, bố cục Văn – Chân trời sáng tạo SBT Văn – Cánh diều Xem thêmMôn Tiếng Anh Lớp 8Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Đề thi, đề kiểm tra Tiếng Anh 8 mới Lý thuyết Tiếng Anh 8 Tiếng Anh – English Discovery SBT Global Success SBT Friends Plus Xem thêmMôn GDCD Lớp 8Giáo dục công dân – Kết nối tri thức Giáo dục công dân – Chân trời sáng tạo Giáo dục công dân – Cánh diềuMôn Công nghệ Lớp 8SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 8SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 8SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diều SGK Giáo dục thể chất – Chân trời sáng tạoMôn Khoa học tự nhiên Lớp 8Vở thực hành Khoa học tự nhiên Đề thi, đề kiểm tra KHTN – Kết nối tri thức Đề thi, đề kiểm tra KHTN – Cánh diều Lý thuyết Khoa học tự nhiên 8 Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Bài tập trắc nghiệm Khoa học tự nhiên – Cánh diều SGK Khoa học tự nhiên – Kết nối tri thức SGK Khoa học tự nhiên – Cánh diều SBT KHTN – Kết nối tri thức Xem thêmMôn Lịch sử và Địa lí Lớp 8Đề thi, kiểm tra Lịch sử và Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Lịch Sử và Địa lí – Cánh diều SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Cánh diều SGK Lịch sử và Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Lịch Sử và Địa lí – Kết nối tri thức
HỌC NGAY
Môn Toán học Lớp 8SBT Toán – Kết nối tri thức SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Vở thực hành Toán Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Lý thuyết Toán 8 Bài tập trắc nghiệm Toán – Kết nối tri thức Xem thêmMôn Ngữ văn Lớp 8Soạn văn chi tiết – Cánh diều Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Soạn văn siêu ngắn – Cánh diều Tóm tắt, bố cục Văn – Kết nối tri thức SBT Văn – Kết nối tri thức Tóm tắt, bố cục Văn – Cánh diều SBT Văn – Chân trời sáng tạo Tóm tắt, bố cục Văn – Chân trời sáng tạo SBT Văn – Cánh diều Xem thêmMôn Tiếng Anh Lớp 8Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Đề thi, đề kiểm tra Tiếng Anh 8 mới Lý thuyết Tiếng Anh 8 Tiếng Anh – English Discovery SBT Global Success SBT Friends Plus Xem thêmMôn GDCD Lớp 8Giáo dục công dân – Kết nối tri thức Giáo dục công dân – Chân trời sáng tạo Giáo dục công dân – Cánh diềuMôn Công nghệ Lớp 8SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 8SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 8SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diều SGK Giáo dục thể chất – Chân trời sáng tạoMôn Khoa học tự nhiên Lớp 8Vở thực hành Khoa học tự nhiên Đề thi, đề kiểm tra KHTN – Kết nối tri thức Đề thi, đề kiểm tra KHTN – Cánh diều Lý thuyết Khoa học tự nhiên 8 Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Bài tập trắc nghiệm Khoa học tự nhiên – Cánh diều SGK Khoa học tự nhiên – Kết nối tri thức SGK Khoa học tự nhiên – Cánh diều SBT KHTN – Kết nối tri thức Xem thêmMôn Lịch sử và Địa lí Lớp 8Đề thi, kiểm tra Lịch sử và Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Lịch Sử và Địa lí – Cánh diều SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Cánh diều SGK Lịch sử và Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Lịch Sử và Địa lí – Kết nối tri thức HỌC NGAY
Môn Toán học Lớp 7SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Lý thuyết Toán 7 Xem thêmMôn Ngữ văn Lớp 7Lý thuyết Văn 7 SBT Văn – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Kết nối tri thức Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Cánh diều Bài tập trắc nghiệm Văn – Kết nối tri thức Bài tập trắc nghiệm Văn – Chân trời sáng tạo Bài tập trắc nghiệm Văn – Cánh diều Vở thực hành văn Xem thêmMôn Tiếng Anh Lớp 7Bài tập trắc nghiệm Tiếng Anh – Friends Plus Bài tập trắc nghiệm Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Lý thuyết Tiếng Anh 7 Tiếng Anh – Right on! Xem thêmMôn Công nghệ Lớp 7SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn Tin học Lớp 7SGK Tin học – Kết nối tri thức SGK Tin học – Cánh Diều SGK Tin học – Chân trời sáng tạo SBT Tin học – Kết nối tri thứcMôn HĐ trải nghiệm, hướng nghiệp Lớp 7SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh Diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạoMôn Khoa học tự nhiên Lớp 7SBT KHTN – Chân trời sáng tạo SBT KHTN – Cánh diều Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Bài tập trắc nghiệm Khoa học tự nhiên – Chân trời sáng tạo Bài tập trắc nghiệm Khoa học tự nhiên – Cánh diều Đề thi, đề kiểm tra KHTN – Kết nối tri thức Đề thi, đề kiểm tra KHTN – Chân trời sáng tạo Đề thi, đề kiểm tra KHTN – Cánh Diều Vở thực hành Khoa học tự nhiên 7 Xem thêmMôn Lịch sử và Địa lí Lớp 7SBT Lịch sử và Địa lí – Chân trời sáng tạo SBT Lịch sử và Địa lí – Cánh diều Đề thi, kiểm tra Lịch sử và Địa lí lớp 7 – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí lớp 7 – Chân trời sáng tạo SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Chân trời sáng tạo SGK Lịch sử và Địa lí – Cánh Diều SBT Lịch sử và Địa lí – Kết nối tri thức
HỌC NGAY
Môn Toán học Lớp 7SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Lý thuyết Toán 7 Xem thêmMôn Ngữ văn Lớp 7Lý thuyết Văn 7 SBT Văn – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Kết nối tri thức Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Cánh diều Bài tập trắc nghiệm Văn – Kết nối tri thức Bài tập trắc nghiệm Văn – Chân trời sáng tạo Bài tập trắc nghiệm Văn – Cánh diều Vở thực hành văn Xem thêmMôn Tiếng Anh Lớp 7Bài tập trắc nghiệm Tiếng Anh – Friends Plus Bài tập trắc nghiệm Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Lý thuyết Tiếng Anh 7 Tiếng Anh – Right on! Xem thêmMôn Công nghệ Lớp 7SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn Tin học Lớp 7SGK Tin học – Kết nối tri thức SGK Tin học – Cánh Diều SGK Tin học – Chân trời sáng tạo SBT Tin học – Kết nối tri thứcMôn HĐ trải nghiệm, hướng nghiệp Lớp 7SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh Diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạoMôn Khoa học tự nhiên Lớp 7SBT KHTN – Chân trời sáng tạo SBT KHTN – Cánh diều Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Bài tập trắc nghiệm Khoa học tự nhiên – Chân trời sáng tạo Bài tập trắc nghiệm Khoa học tự nhiên – Cánh diều Đề thi, đề kiểm tra KHTN – Kết nối tri thức Đề thi, đề kiểm tra KHTN – Chân trời sáng tạo Đề thi, đề kiểm tra KHTN – Cánh Diều Vở thực hành Khoa học tự nhiên 7 Xem thêmMôn Lịch sử và Địa lí Lớp 7SBT Lịch sử và Địa lí – Chân trời sáng tạo SBT Lịch sử và Địa lí – Cánh diều Đề thi, kiểm tra Lịch sử và Địa lí lớp 7 – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí lớp 7 – Chân trời sáng tạo SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Chân trời sáng tạo SGK Lịch sử và Địa lí – Cánh Diều SBT Lịch sử và Địa lí – Kết nối tri thức HỌC NGAY
Môn Toán học Lớp 6SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Tài liệu Dạy – học Toán 6 Ôn tập hè Toán lớp 6 Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Xem thêmMôn Ngữ văn Lớp 6Ôn tập hè Văn lớp 6 Vở thực hành văn Soạn văn siêu ngắn – Cánh diều Soạn văn chi tiết – Cánh diều Tác giả – Tác phẩm văn 6 SBT Văn – Kết nối tri thức SBT Văn – Chân trời sáng tạo SBT Văn – Cánh diều Bài tập trắc nghiệm Văn – Kết nối tri thức Xem thêmMôn Tiếng Anh Lớp 6Đề thi, đề kiểm tra Tiếng Anh – English Discovery Ôn tập hè Tiếng Anh lớp 6 Bài tập trắc nghiệm Tiếng Anh 6 – English Discovery Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Right on! Tiếng Anh – English Discovery Tiếng Anh – Explore English Xem thêmMôn GDCD Lớp 6SBT GDCD – Chân trời sáng tạo SBT GDCD – Cánh diều SGK GDCD – CTST SGK GDCD – Cánh Diều SBT GDCD – Kết nối tri thức SGK GDCD – KNTTMôn Công nghệ Lớp 6SBT Công nghệ – Cánh diều SBT Công nghệ – Chân trời sáng tạo Công nghệ – Kết nối tri thức Công nghệ – Cánh Diều Công nghệ – Chân trời sáng tạo SBT Công nghệ – Kết nối tri thứcMôn Tin học Lớp 6Tin học – Kết nối tri thức + chân trời sáng tạo Tin học – Cánh Diều SBT Tin học – Kết nối tri thức SBT Tin học – Cánh DiềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 6SBT Trải nghiệm, hướng nghiệp – Chân trời sáng tạo Thực hành Trải nghiệm, hướng nghiệp – Cánh diều SGK Trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Trải nghiệm, hướng nghiệp – Chân trời sáng tạo SGK Trải nghiệm, hướng nghiệp – Cánh diều SBT Trải nghiệm, hướng nghiệp – Kết nối tri thứcMôn Khoa học tự nhiên Lớp 6SBT KHTN – Chân trời sáng tạo SBT KHTN – Cánh Diều Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Bài tập trắc nghiệm Khoa học tự nhiên – Chân trời sáng tạo Bài tập trắc nghiệm Khoa học tự nhiên – Cánh diều Đề thi, đề kiểm tra KHTN – Kết nối tri thức Đề thi, đề kiểm tra KHTN – Chân trời sáng tạo Đề thi, đề kiểm tra KHTN – Cánh diều Vở thực hành Khoa học tự nhiên 6 Xem thêmMôn Lịch sử và Địa lí Lớp 6SBT Lịch sử và Địa lí – CTST SBT Lịch sử và Địa lí – Cánh diều Đề thi, kiểm tra Lịch sử và Địa lí – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí – Cánh Diều Đề thi, kiểm tra Lịch sử và Địa lí – Chân trời sáng tạo SGK Lịch sử và Địa lí – KNTT SGK Lịch sử và Địa lí – CTST SGK Lịch sử và Địa lí – Cánh Diều SBT Lịch sử và Địa lí – KNTTMôn Mỹ thuật Lớp 6Mĩ thuật – Kết nối tri thức Mĩ thuật – Chân trời sáng tạo Mĩ thuật – Cánh diều
HỌC NGAY
Môn Toán học Lớp 6SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Tài liệu Dạy – học Toán 6 Ôn tập hè Toán lớp 6 Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Xem thêmMôn Ngữ văn Lớp 6Ôn tập hè Văn lớp 6 Vở thực hành văn Soạn văn siêu ngắn – Cánh diều Soạn văn chi tiết – Cánh diều Tác giả – Tác phẩm văn 6 SBT Văn – Kết nối tri thức SBT Văn – Chân trời sáng tạo SBT Văn – Cánh diều Bài tập trắc nghiệm Văn – Kết nối tri thức Xem thêmMôn Tiếng Anh Lớp 6Đề thi, đề kiểm tra Tiếng Anh – English Discovery Ôn tập hè Tiếng Anh lớp 6 Bài tập trắc nghiệm Tiếng Anh 6 – English Discovery Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Right on! Tiếng Anh – English Discovery Tiếng Anh – Explore English Xem thêmMôn GDCD Lớp 6SBT GDCD – Chân trời sáng tạo SBT GDCD – Cánh diều SGK GDCD – CTST SGK GDCD – Cánh Diều SBT GDCD – Kết nối tri thức SGK GDCD – KNTTMôn Công nghệ Lớp 6SBT Công nghệ – Cánh diều SBT Công nghệ – Chân trời sáng tạo Công nghệ – Kết nối tri thức Công nghệ – Cánh Diều Công nghệ – Chân trời sáng tạo SBT Công nghệ – Kết nối tri thứcMôn Tin học Lớp 6Tin học – Kết nối tri thức + chân trời sáng tạo Tin học – Cánh Diều SBT Tin học – Kết nối tri thức SBT Tin học – Cánh DiềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 6SBT Trải nghiệm, hướng nghiệp – Chân trời sáng tạo Thực hành Trải nghiệm, hướng nghiệp – Cánh diều SGK Trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Trải nghiệm, hướng nghiệp – Chân trời sáng tạo SGK Trải nghiệm, hướng nghiệp – Cánh diều SBT Trải nghiệm, hướng nghiệp – Kết nối tri thứcMôn Khoa học tự nhiên Lớp 6SBT KHTN – Chân trời sáng tạo SBT KHTN – Cánh Diều Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Bài tập trắc nghiệm Khoa học tự nhiên – Chân trời sáng tạo Bài tập trắc nghiệm Khoa học tự nhiên – Cánh diều Đề thi, đề kiểm tra KHTN – Kết nối tri thức Đề thi, đề kiểm tra KHTN – Chân trời sáng tạo Đề thi, đề kiểm tra KHTN – Cánh diều Vở thực hành Khoa học tự nhiên 6 Xem thêmMôn Lịch sử và Địa lí Lớp 6SBT Lịch sử và Địa lí – CTST SBT Lịch sử và Địa lí – Cánh diều Đề thi, kiểm tra Lịch sử và Địa lí – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí – Cánh Diều Đề thi, kiểm tra Lịch sử và Địa lí – Chân trời sáng tạo SGK Lịch sử và Địa lí – KNTT SGK Lịch sử và Địa lí – CTST SGK Lịch sử và Địa lí – Cánh Diều SBT Lịch sử và Địa lí – KNTTMôn Mỹ thuật Lớp 6Mĩ thuật – Kết nối tri thức Mĩ thuật – Chân trời sáng tạo Mĩ thuật – Cánh diều HỌC NGAY
Môn Toán học Lớp 5Cùng em học toán lớp 5 Bài tập trắc nghiệm Toán 5 Đề thi, đề kiểm tra Toán lớp 5 Bài tập phát triển năng lực Toán lớp 5 Toán nâng cao lớp 5 Công thức Toán lớp 5 Đề thi vào lớp 6 môn Toán SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo Xem thêmMôn Tiếng Anh Lớp 5Đề thi, đề kiểm tra Tiếng Anh lớp 5 Tiếng Anh – Global Success Tiếng Anh – Family and Friends Tiếng Anh – iLearn Smart Start Tiếng Anh – Explore Our World SGK Tiếng Anh lớp 5 Mới Đề thi vào lớp 6 môn Tiếng Anh Chứng chỉ Cambridge Pre A1 Starters SBT Tiếng Anh lớp 5Môn Lịch sử và Địa lí Lớp 5SGK Lịch sử và Địa lí lớp 5 Vở bài tập Lịch sử lớp 5 Vở bài tập Địa lí lớp 5
HỌC NGAY
Môn Toán học Lớp 5Cùng em học toán lớp 5 Bài tập trắc nghiệm Toán 5 Đề thi, đề kiểm tra Toán lớp 5 Bài tập phát triển năng lực Toán lớp 5 Toán nâng cao lớp 5 Công thức Toán lớp 5 Đề thi vào lớp 6 môn Toán SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo Xem thêmMôn Tiếng Anh Lớp 5Đề thi, đề kiểm tra Tiếng Anh lớp 5 Tiếng Anh – Global Success Tiếng Anh – Family and Friends Tiếng Anh – iLearn Smart Start Tiếng Anh – Explore Our World SGK Tiếng Anh lớp 5 Mới Đề thi vào lớp 6 môn Tiếng Anh Chứng chỉ Cambridge Pre A1 Starters SBT Tiếng Anh lớp 5Môn Lịch sử và Địa lí Lớp 5SGK Lịch sử và Địa lí lớp 5 Vở bài tập Lịch sử lớp 5 Vở bài tập Địa lí lớp 5 HỌC NGAY
Môn Toán học Lớp 4VBT Toán – Kết nối tri thức Vở thực hành Toán Bài tập phát triển năng lực Toán lớp 4 Bài tập cuối tuần Toán 4 Ôn tập hè Toán lớp 4 Cùng em học toán lớp 4 Đề thi, đề kiểm tra Toán lớp 4 Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Cánh diều Xem thêmMôn Tiếng Anh Lớp 4Tiếng Anh – Explore Our World SGK Tiếng Anh lớp 4 Mới SBT Tiếng Anh – Global Success Ôn tập hè Tiếng Anh lớp 4 SBT Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh lớp 4 SBT Tiếng Anh – iLearn Smart Start SBT Tiếng Anh – Phonics Smart SBT Tiếng Anh – Explore Our World Xem thêmMôn Công nghệ Lớp 4SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 4SGK Hoạt động trải nghiệm – Kết nối tri thức SGK Hoạt động trải nghiệm – Cánh diều SGK Hoạt động trải nghiệm – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 4SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diều SGK Giáo dục thể chất – Chân trời sáng tạoMôn Lịch sử và Địa lí Lớp 4SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Chân trời sáng tạo SGK Lịch sử và Địa lí – Cánh diềuMôn Âm nhạc Lớp 4SGK Âm nhạc – Kết nối tri thức SGK Âm nhạc – Chân trời sáng tạo SGK Âm nhạc – Cánh diềuMôn Mỹ thuật Lớp 4SGK Mĩ thuật – Kết nối tri thức SGK Mĩ thuật – Cánh diều SGK Mĩ thuật – Chân trời sáng tạo bản 1 SGK Mĩ thuật – Chân trời sáng tạo bản 2Môn Tiếng việt Lớp 4Đề thi, đề kiểm tra Tiếng Việt – Kết nối tri thức Đề thi, đề kiểm tra Tiếng Việt – Chân trời sáng tạo Đề thi, đề kiểm tra Tiếng Việt – Cánh diều SGK Tiếng Việt 4 Cùng em học Tiếng Việt 4 Vở bài tập Tiếng Việt lớp 4 VNEN Tiếng Việt lớp 4 Văn mẫu lớp 4 Đề thi, đề kiểm tra Tiếng Việt 4 Xem thêm
HỌC NGAY
Môn Toán học Lớp 4VBT Toán – Kết nối tri thức Vở thực hành Toán Bài tập phát triển năng lực Toán lớp 4 Bài tập cuối tuần Toán 4 Ôn tập hè Toán lớp 4 Cùng em học toán lớp 4 Đề thi, đề kiểm tra Toán lớp 4 Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Cánh diều Xem thêmMôn Tiếng Anh Lớp 4Tiếng Anh – Explore Our World SGK Tiếng Anh lớp 4 Mới SBT Tiếng Anh – Global Success Ôn tập hè Tiếng Anh lớp 4 SBT Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh lớp 4 SBT Tiếng Anh – iLearn Smart Start SBT Tiếng Anh – Phonics Smart SBT Tiếng Anh – Explore Our World Xem thêmMôn Công nghệ Lớp 4SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 4SGK Hoạt động trải nghiệm – Kết nối tri thức SGK Hoạt động trải nghiệm – Cánh diều SGK Hoạt động trải nghiệm – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 4SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diều SGK Giáo dục thể chất – Chân trời sáng tạoMôn Lịch sử và Địa lí Lớp 4SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Chân trời sáng tạo SGK Lịch sử và Địa lí – Cánh diềuMôn Âm nhạc Lớp 4SGK Âm nhạc – Kết nối tri thức SGK Âm nhạc – Chân trời sáng tạo SGK Âm nhạc – Cánh diềuMôn Mỹ thuật Lớp 4SGK Mĩ thuật – Kết nối tri thức SGK Mĩ thuật – Cánh diều SGK Mĩ thuật – Chân trời sáng tạo bản 1 SGK Mĩ thuật – Chân trời sáng tạo bản 2Môn Tiếng việt Lớp 4Đề thi, đề kiểm tra Tiếng Việt – Kết nối tri thức Đề thi, đề kiểm tra Tiếng Việt – Chân trời sáng tạo Đề thi, đề kiểm tra Tiếng Việt – Cánh diều SGK Tiếng Việt 4 Cùng em học Tiếng Việt 4 Vở bài tập Tiếng Việt lớp 4 VNEN Tiếng Việt lớp 4 Văn mẫu lớp 4 Đề thi, đề kiểm tra Tiếng Việt 4 Xem thêm HỌC NGAY
Môn Toán học Lớp 3Đề thi, đề kiểm tra Toán – Kết nối tri thức Bài tập cuối tuần môn Toán 3 Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Cùng em học Toán 3 Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Ôn tập hè Toán – Kết nối tri thức Xem thêmMôn Tiếng Anh Lớp 3Bài tập trắc nghiệm Tiếng Anh – iLearn Smart Start Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh – Explore Our World Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart Start Đề thi, đề kiểm tra Tiếng Anh – Phonics Smart Chứng chỉ Cambridge Pre A1 Starters Tiếng Anh – Phonics Smart SBT Tiếng Anh – Global Success Xem thêmMôn Tin học Lớp 3SGK Tin học – Kết nối tri thức SGK Tin học – Chân trời sáng tạo SGK Tin học – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 3SGK Hoạt động trải nghiệm- Kết nối tri thức SGK Hoạt động trải nghiệm- Chân trời sáng tạo SGK Hoạt động trải nghiệm – Cánh diềuMôn Tiếng việt Lớp 3VBT Tiếng Việt – Chân trời sáng tạo VBT Tiếng Việt – Cánh diều Văn mẫu – Kết nối tri thức Cùng em học Tiếng Việt 3 Văn mẫu lớp 3 Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh diều VBT Tiếng Việt – Kết nối tri thứcMôn Tự nhiên và xã hội Lớp 3Tự nhiên và xã hội – Kết nối tri thức Tự nhiên và xã hội – Chân trời sáng tạo Tự nhiên và xã hội – Cánh diều
HỌC NGAY
Môn Toán học Lớp 3Đề thi, đề kiểm tra Toán – Kết nối tri thức Bài tập cuối tuần môn Toán 3 Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Cùng em học Toán 3 Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Ôn tập hè Toán – Kết nối tri thức Xem thêmMôn Tiếng Anh Lớp 3Bài tập trắc nghiệm Tiếng Anh – iLearn Smart Start Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh – Explore Our World Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart Start Đề thi, đề kiểm tra Tiếng Anh – Phonics Smart Chứng chỉ Cambridge Pre A1 Starters Tiếng Anh – Phonics Smart SBT Tiếng Anh – Global Success Xem thêmMôn Tin học Lớp 3SGK Tin học – Kết nối tri thức SGK Tin học – Chân trời sáng tạo SGK Tin học – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 3SGK Hoạt động trải nghiệm- Kết nối tri thức SGK Hoạt động trải nghiệm- Chân trời sáng tạo SGK Hoạt động trải nghiệm – Cánh diềuMôn Tiếng việt Lớp 3VBT Tiếng Việt – Chân trời sáng tạo VBT Tiếng Việt – Cánh diều Văn mẫu – Kết nối tri thức Cùng em học Tiếng Việt 3 Văn mẫu lớp 3 Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh diều VBT Tiếng Việt – Kết nối tri thứcMôn Tự nhiên và xã hội Lớp 3Tự nhiên và xã hội – Kết nối tri thức Tự nhiên và xã hội – Chân trời sáng tạo Tự nhiên và xã hội – Cánh diều HỌC NGAY
Môn Toán học Lớp 2VBT Toán – CTST Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Cùng em học Toán 2 Bài tập cuối tuần Toán 2 Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Xem thêmMôn Tiếng Anh Lớp 2SBT Kết nối tri thức SBT Family and Friends SBT iLearn Smart Start SBT Phonics Smart SBT English Discovery SBT Explore Our World Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart Start Xem thêmMôn HĐ trải nghiệm, hướng nghiệp Lớp 2VBT Hoạt động trải nghiệm – Chân trời sáng tạo VTH Hoạt động trải nghiệm – Cánh Diều VBT Hoạt động trải nghiệm – Kết nối tri thứcMôn Âm nhạc Lớp 2VBT Âm nhạc – Chân trời sáng tạo VBT Âm nhạc – Cánh diều Âm nhạc 2 – Kết nối tri thức Âm nhạc 2 – Chân trời sáng tạo Âm nhạc 2 – Cánh diều VBT Âm nhạc – Kết nối tri thứcMôn Tiếng việt Lớp 2Văn mẫu – Chân trời sáng tạo Văn mẫu – Cánh diều VBT Tiếng Việt – Kết nối tri thức VBT Tiếng Việt – Chân trời sáng tạo VBT Tiếng Việt – Cánh diều Cùng em học Tiếng Việt 2 Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh Diều Xem thêm
HỌC NGAY
Môn Toán học Lớp 2VBT Toán – CTST Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Cùng em học Toán 2 Bài tập cuối tuần Toán 2 Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Xem thêmMôn Tiếng Anh Lớp 2SBT Kết nối tri thức SBT Family and Friends SBT iLearn Smart Start SBT Phonics Smart SBT English Discovery SBT Explore Our World Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart Start Xem thêmMôn HĐ trải nghiệm, hướng nghiệp Lớp 2VBT Hoạt động trải nghiệm – Chân trời sáng tạo VTH Hoạt động trải nghiệm – Cánh Diều VBT Hoạt động trải nghiệm – Kết nối tri thứcMôn Âm nhạc Lớp 2VBT Âm nhạc – Chân trời sáng tạo VBT Âm nhạc – Cánh diều Âm nhạc 2 – Kết nối tri thức Âm nhạc 2 – Chân trời sáng tạo Âm nhạc 2 – Cánh diều VBT Âm nhạc – Kết nối tri thứcMôn Tiếng việt Lớp 2Văn mẫu – Chân trời sáng tạo Văn mẫu – Cánh diều VBT Tiếng Việt – Kết nối tri thức VBT Tiếng Việt – Chân trời sáng tạo VBT Tiếng Việt – Cánh diều Cùng em học Tiếng Việt 2 Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh Diều Xem thêm HỌC NGAY
Môn Tiếng Anh Lớp 1Chứng chỉ Cambridge Pre A1 StartersMôn Tiếng việt Lớp 1Đề thi, đề kiểm tra Tiếng Việt 1 SGK Tiếng Việt – Kết nối tri thức SGK Tiếng Việt – Chân trời sáng tạo SGK Tiếng Việt – Cánh diềuMôn Đạo đức Lớp 1VBT Đạo Đức 1
HỌC NGAY
Môn Tiếng Anh Lớp 1Chứng chỉ Cambridge Pre A1 StartersMôn Tiếng việt Lớp 1Đề thi, đề kiểm tra Tiếng Việt 1 SGK Tiếng Việt – Kết nối tri thức SGK Tiếng Việt – Chân trời sáng tạo SGK Tiếng Việt – Cánh diềuMôn Đạo đức Lớp 1VBT Đạo Đức 1














 hoặc
hoặc 



