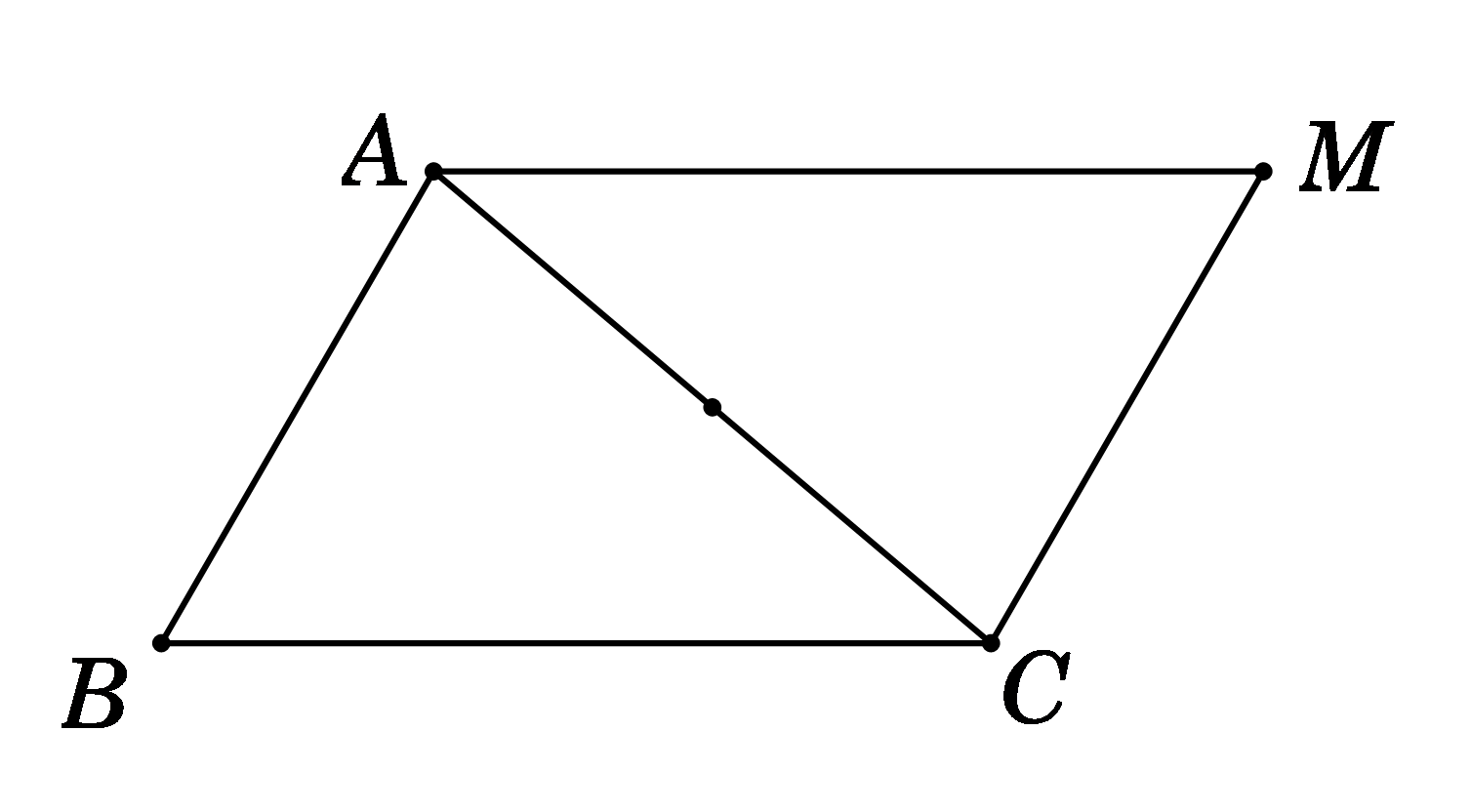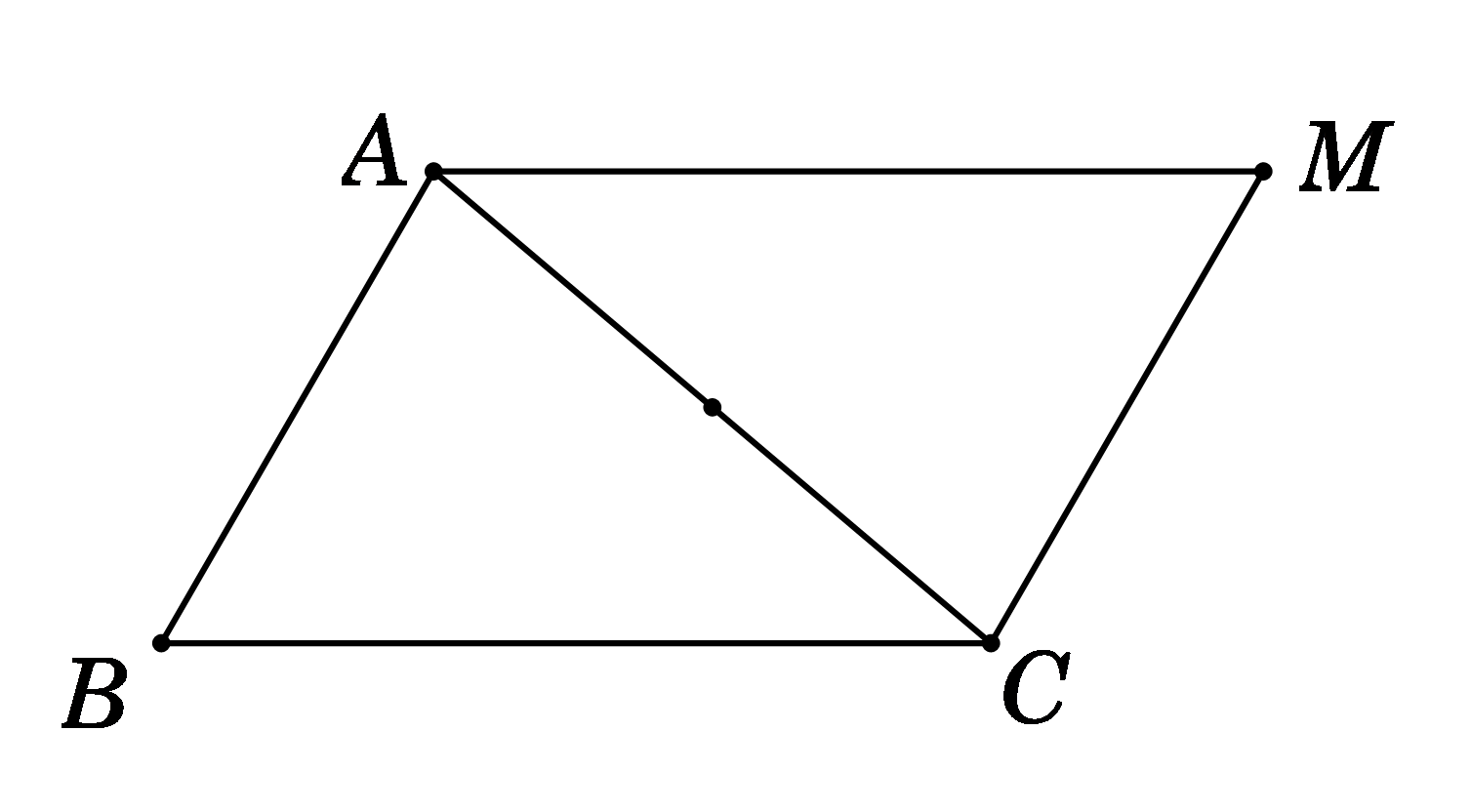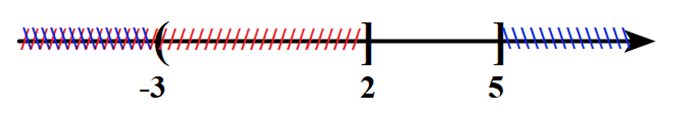Lựa chọn câu để xem lời giải nhanh hơn
Đề 1
Phần 1: Trắc nghiệm (30 câu – 6 điểm)
Câu 1: Câu nào sau đây không phải là mênh đề?
A. Bạn bao nhiêu tuổi? B. Hôm nay là chủ nhật. C. Trái đất hình tròn. D. 4 \ne 5.
Câu 2: Cho số \(\bar a = 31975421 \pm 150\). Hãy viết số quy tròn của số 31975421.
A. 31975400. B. 31976000. C. 31970000. D. 31975000.
Câu 3: Cho tam giác ABC có M, N, Q lần lượt là trung điểm của AB, BC, CA. Khi đó vectơ \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BM} {\rm{ \;}} + \overrightarrow {NA} {\rm{ \;}} + \overrightarrow {BQ} \) bằng vectơ nào sau đây?
A. \(\overrightarrow {CB} .\) B. \(\overrightarrow {BA} .\) C. \(\vec 0.\) D. \(\overrightarrow {BC} .\)
Câu 4: Cho tam giác ABC có AB = 6, AC = 8 và \(\angle BAC = {120^0}\). Độ dài cạnh BC bằng:
A. 10. B. \(2\sqrt {13} .\) C. 12. D. \(2\sqrt {37} .\)
Câu 5: Cặp số (x;y) nào là sau đây là một nghiệm của bất phương trình x – y + 3 > 0.
A. (x;y) = (0;4). B. (x;y) = (2;5). C. (x;y) = (1;3). D. (x;y) = (1;4).
Câu 6: Cho hình bình hành ABCD. Nếu viết được \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} {\rm{ \;}} + \overrightarrow {AD} {\rm{ \;}} = k\overrightarrow {AC} \) thì k bằng
A. 4. B. 3. C. 2. D. 1.
Câu 7: Gọi a, b, c, r, R, S lần lượt là độ dài ba cạnh, bán kính đường tròn nội tiếp, ngoại tiếp và diện tích của tam giác ABC. Khẳng định nào sau đây là đúng
A. \(S = p.R\) với \(p = \frac{{a + b + c}}{2}.\)
B. \(S = \frac{{abc}}{{4R}}\).
C. \(S = \frac{1}{2}\sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} \) với \(p = \frac{{a + b + c}}{2}.\)
D. \(S = \frac{1}{2}ab\cos C\).
Câu 8: Tính số đo góc B của tam giác ABC có các cạnh BC = a, AC = b, AB = c thỏa mãn \({a^4} + {b^4} + {c^4} + {a^2}{c^2} – 2{a^2}{b^2} – 2{b^2}{c^2} = 0.\)
A. 300. B. 300 hoặc 1500. C. 600. D. 600 hoặc 1200.
Câu 9: Cho hai tập hợp \(P = \left[ { – 4;5} \right)\) và \(Q = \left( { – 3; + \infty } \right)\). Khẳng định nào sau đây là đúng?
A. \(P\backslash Q = \left[ { – 4; – 3} \right].\) B. \(P \cap Q = \left( { – 3;5} \right].\)
C. \(P \cup Q = \left[ { – 4;5} \right).\) D. \({C_\mathbb{R}}P = \left( { – \infty ; – 4} \right] \cup \left[ {5; + \infty } \right).\)
Câu 10: Cho các tập hợp A, B, C được minh họa bằng biểu đồ Ven như hình vẽ. Phần tô màu xám trong hình là biểu diễn của tập hợp nào sau đây?
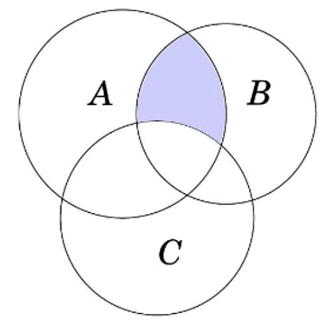
A. \(A \cap B \cap C.\) B. \(\left( {A\backslash C} \right) \cup \left( {A\backslash B} \right).\) C. \(\left( {A \cup B} \right)\backslash C.\) D. \(\left( {A \cap B} \right)\backslash C.\)
Câu 11: Khoảng cách từ điểm A đến điểm B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 52016’. Biết CA = 200m, BC = 180m. Tính khoảng cách từ A đến B (làm tròn đến hàng đơn vị).
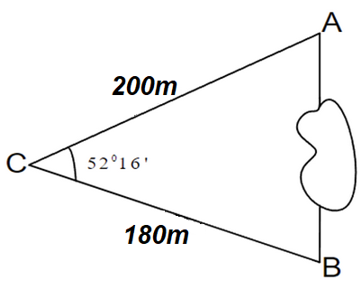
A. 165m. B. 166m. C. 169m. D. 168m.
Câu 12: Biết \(\sin x = \frac{1}{2}\). Giá trị của biểu thức \(P = {\sin ^2}x – {\cos ^2}x\) là
A. \(\frac{1}{2}\) B. \( – \frac{1}{2}\) C. \( – \frac{1}{2} + \frac{{\sqrt 3 }}{2}\) D. \( – \frac{1}{2} – \frac{{\sqrt 3 }}{2}\)
Câu 13: Cho \(A = \left\{ {x \in \mathbb{R}| – 1 < x < 4} \right\}\), \(B = \left\{ {x \in \mathbb{R}|\left| x \right| \le 3} \right\}\). Khi đó \(A \cap B\) là:
A. \(\left[ { – 1;3} \right].\) B. \(\left( { – 1;3} \right].\) C. \(\left[ { – 3;4} \right].\) D. \(\left[ {3;4} \right).\)
Câu 14: Giá trị của biểu thức \(A = {\sin ^2}{51^0} + {\sin ^2}{55^0} + {\sin ^2}{39^0} + {\sin ^2}{35^0}\) là:
A. 3. B. 4. C. 1. D. 2.
Câu 15: Cho ba lực \(\overrightarrow {{F_1}} {\rm{ \;}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} {\rm{ \;}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} {\rm{ \;}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {{F_2}} \) đều bằng 100N và \(\angle AMB = {60^0}\). Khi đó cường độ lực \(\overrightarrow {{F_3}} \) là:
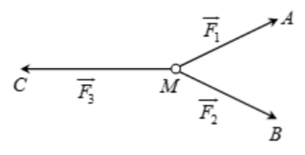
A. \(50\sqrt 2 N\). B. \(50\sqrt 3 N\). C. \(25\sqrt 3 N\). D. \(100\sqrt 3 N\).
Câu 16: Mệnh đề nào sau đây là sai?
A. \(\vec a{\rm{ \;}} \ne 0 \Leftrightarrow \left| {\vec a} \right| \ne 0\). B. Cho ba điểm A, B, C phân biệt thẳng hàng, \(\overrightarrow {CA} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {CB} \) cùng hướng khi và chỉ khi C nằm ngoài đoạn AB. C. \(\vec a,{\mkern 1mu} {\mkern 1mu} \vec b\) cùng phương với \(\vec c\) thì \(\vec a,{\mkern 1mu} {\mkern 1mu} \vec b\) cùng phương. D. \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AC} } \right|\).
Câu 17: Trên \(2\) con đường A và B, trạm kiểm soát đã ghi lại tốc độ \(\left( {{\rm{km/h}}} \right)\) của 20 chiếc xe ô tô trên mỗi con đường như sau:
Con đường A:
\(\begin{array}{*{20}{c}}{60}&{65}&{76}&{68}&{65}&{75}&{80}&{80}&{68}&{60}\\{65}&{90}&{90}&{85}&{65}&{72}&{75}&{76}&{85}&{84}\end{array}\)
Con đường B:
\(\begin{array}{*{20}{c}}{76}&{64}&{85}&{60}&{70}&{62}&{70}&{55}&{79}&{80}\\{79}&{62}&{55}&{70}&{64}&{76}&{80}&{79}&{55}&{85}\end{array}\)
Với bảng số liệu như trên thì chạy xe trên con đường nào sẽ an toàn hơn?
A. Con đường A B. Con đường B C. Như nhau D. Không kết luận được
Câu 18: Giả sử ta có một mẫu số liệu kích thước \(N\) là \(\left\{ {{x_1};{\mkern 1mu} {\mkern 1mu} {x_2};{\mkern 1mu} {\mkern 1mu} \ldots ;{\mkern 1mu} {\mkern 1mu} {x_N}} \right\}\). Khi đó, phương sai của mẫu số liệu này, kí hiệu là \({s^2}\) được tính bởi công thức nào sau đây?
A. \({s^2} = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{x_i} – \bar x} \right)}^2}} \) B. \({s^2} = \frac{1}{N}{\left( {\sum\limits_{i = 1}^N {\left( {{x_i} – \bar x} \right)} } \right)^2}\) C. \({s^2} = N\sum\limits_{i = 1}^N {{{\left( {{x_i} – \bar x} \right)}^2}} \) D. \({s^2} = N{\left( {\sum\limits_{i = 1}^N {\left( {{x_i} – \bar x} \right)} } \right)^2}\)
Câu 19: Cho tam giác ABC vuông cân tại A có AB = 4. Giá trị của \(\overrightarrow {BA} .\overrightarrow {BC} \) bằng
A. 0. B. 16. C. -16. D. \(16\sqrt 2 .\)
Câu 20: Một cửa hàng bán sách thống kê số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở cửa hàng trong một ngày. Số liệu được ghi trong bảng phân bố tần số sau:
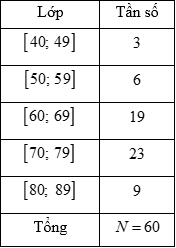
Số trung bình cộng và độ lệch chuẩn xấp xỉ bằng (kết quả được làm tròn đến chữ số thập phân thứ hai).
A. 69,34 và 10,26 B. 69,33 và 10,25 C. 10,25 và 69,33 D. 10,26 và 69,34
Câu 21: Đường thẳng \( – x + 3y > 2\) chia mặt phẳng tọa độ thành các miền như hình vẽ. Xác định miền nghiệm của \( – x + 3y > 2\).
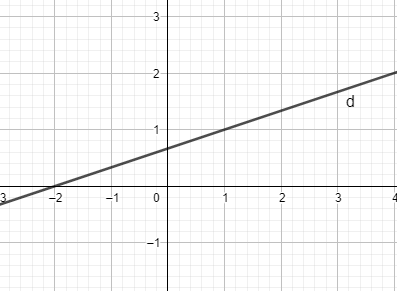
A. Nửa mặt phẳng có bờ là d cùng phía gốc tọa độ O và có lấy đường thẳng d.
B. Nửa mặt phẳng có bờ là d khác phía gốc tọa độ O và có lấy đường thẳng d.
C. Nửa mặt phẳng có bờ là d cùng phía gốc tọa độ O và không lấy đường thẳng d.
D. Nửa mặt phẳng có bờ là d khác phía gốc tọa độ O và không lấy đường thẳng d.
Câu 22: Điểm nào dưới đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 2y > {\rm{ \;}} – 4}\\{3x – y < 5}\\{x + 1 > 0}\end{array}} \right.\).
A. \(\left( { – 2, – 3} \right)\) B. \(\left( {2, – 3} \right)\) C. \(\left( {4,0} \right)\) D. \(\left( {0,2} \right)\)
Câu 23: Cho tam giác ABC thỏa mãn hệ thức b + c = 2a. Trong các mệnh đề sau, mệnh đề nào đúng?
A. \(\cos B + \cos C = 2\cos A.\) B. \(\sin B + \sin C = 2\sin A.\)
C. \(\sin B + \sin C = \frac{1}{2}\sin A.\) D. \(\sin B + \cos C = 2\sin A.\)
Câu 24: Cho tam giác đều ABC có độ dài các cạnh bằng 4 và điểm M thỏa mãn \(\overrightarrow {BM} {\rm{ \;}} = {\rm{ \;}} – \frac{1}{2}\overrightarrow {BC} \). Tính tích vô hướng \(\overrightarrow {BM} .\overrightarrow {BA} \).
A. \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = 4.\) B. \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} – 4\sqrt 3 .\) C. \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = 4\sqrt 3 .\) D. \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} – 4.\)
Câu 25: Kết quả đo chiều dài của một cây cầu được ghi là , điều đó có nghĩa là:
A. Chiều dài đúng của cây cầu là một số nằm trong khoảng 151,8m đến 152,2m.
B. Chiều dài đúng của cây cầu là một số lớn hơn 152m.\(152m \pm 0,2m\).
C. Chiều dài đúng của cây cầu là một số nhỏ hơn 152m.
D. Chiều dài đúng của câu cầu là 151,8m hoặc là 152,2m.
Câu 26: Một hình chữ nhật có kích thước \(x = 2m \pm 1cm\) và \(y = 5m \pm 2cm\). Diện tích hình chữ nhật và sai số tuyệt đối của giá trị đó là:
A. 10m2 và 400cm2. B. 10m2 và 500cm2. C. 10m2 và 900cm2. D. 10m2 và 404cm2.
Câu 27: Khoảng biến thiên của mẫu số liệu 10; 13; 15; 2; 10; 19; 2; 5; 7 là:
A. 3. B. 8. C. 17. D. 20.
Câu 28: Trong đợt hội diễn văn nghệ chào mừng 20/11, lớp 10A đăng kí tham gia 3 tiết mục là hát tốp ca, múa và diễn kịch. Trong danh sách đăng kí, có 7 học sinh đăng kí tiết mục hát tốp ca, 6 học sinh đăng kí tiết mục múa, 8 học sinh đăng kí diễn kịch; trong đó có 3 học sinh đăng kí cả tiết mục hát tốp ca và tiết mục múa, 4 học sinh đăng kí cả tiết mục hát tốp ca và diễn kịch, 2 học sinh đăng kí cả tiết mục múa và diễn kịch, 1 học sinh đăng kí cả 3 tiết mục. Hỏi lớp 10A có tất cả bao nhiêu học sinh đăng kí tham gia hội diễn văn nghệ?
A. 14. B. 13. C. 21. D. 11.
Câu 29: Cho hình chữ nhật ABCD biết AB = 4a, AD = 3a. Gọi O là giao điểm của hai đường chéo AC và BD. Tính độ dài \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {OD} \).
A. 7a. B. \(\frac{7}{2}a.\) C. \(\frac{5}{2}a.\) D. 5a.
Câu 30: Cho hai vectơ \(\vec a\) và \(\vec b\) khác \(\vec 0\). Xác định góc \(\alpha \) giữa hai vectơ \(\vec a\) và \(\vec b\) khi \(2\vec a.\vec b{\rm{ \;}} = {\rm{ \;}} – \left| {\vec a} \right|.\left| {\vec b} \right|\).
A. \(\alpha {\rm{ \;}} = {180^0}.\) B. \(\alpha {\rm{ \;}} = {120^0}.\) C. \(\alpha {\rm{ \;}} = {90^0}.\) D. \(\alpha {\rm{ \;}} = {60^0}.\)
Phần 2: Tự luận (4 điểm)
Câu 1: Cho tam giác ABC. Gọi M là điểm thỏa mãn \(3\overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\) và G là trọng tâm của tam giác ABC.
a) Chứng minh rằng \(\overrightarrow {MG} {\rm{ \;}} = \frac{1}{{12}}\overrightarrow {AC} {\rm{ \;}} – \frac{5}{{12}}\overrightarrow {AB} \).
b) Gọi K là giao điểm của hai đường thẳng AC và MG. Tính tỉ số \(\frac{{KA}}{{KC}}.\)
Câu 2: Tổng số ca mắc Covid-19 tính đến ngày 26/8/2021 tại Thành phố Hồ Chí Minh và một số tỉnh lân cận được thống kê như sau:

a) Tính số trung bình và trung vị của dãy số trên.
b) Giải thích tại sao số trung bình và trung vị lại khác nhau nhiều?
Câu 3: Cho tam giác ABC có BC = 3 thỏa mãn \(4\sin A\tan A = \sin B\sin C\). Gọi G là trọng tâm tam giác ABC. Tính giá trị biểu thức \(S = G{B^2} + G{C^2} + 9G{A^2}\).
—– HẾT —–
Giải đề 1
HƯỚNG DẪN GIẢI CHI TIẾT
Phần 1: Trắc nghiệm (30 câu – 6 điểm)
|
1.A
|
2.D
|
3.B
|
4.D
|
5.C
|
6.C
|
7.D
|
8.D
|
9.A
|
10.D
|
|
11.D
|
12.B
|
13.B
|
14.D
|
15.D
|
16.D
|
17.A
|
18.A
|
19.B
|
20.B
|
|
21.D
|
22.D
|
23.B
|
24.B
|
25.A
|
26.C
|
27.C
|
28.B
|
29.C
|
30.B
|
Câu 1 (NB):
Phương pháp:
Mệnh đề là câu khẳng định có tính đúng hoặc sai.
Cách giải:
Bạn bao nhiêu tuổi? là câu nghi vấn nên không phải là mệnh đề.
Chọn A.
Câu 2 (NB):
Phương pháp:
Ta thường dùng các chữ cái in hoa để kí hiệu tập hợp và chữ cái in thường để kí hiệu phần tử thuộc tập hợp.
Cách giải:
Ta có: \(\bar a = 31975421 \pm 150 \Rightarrow \bar a \in \left[ {31975271;31975571} \right]\).
Khi làm tròn số gần đúng a ta nên làm tròn đến hàng nghìn vì chữ số hàng trăm không chắc chắn đúng.
Vậy quy tròn số gần đúng a ta được số 31975000.
Chọn D.
Câu 3 (TH):
Phương pháp:
Sử dụng quy tắc ba điểm.
Sử dụng hai vectơ bằng nhau.
Cách giải:
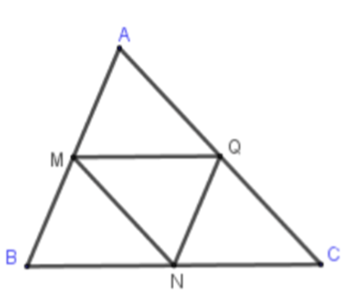
Ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BM} {\rm{ \;}} + \overrightarrow {NA} {\rm{ \;}} + \overrightarrow {BQ} }\\{ = \overrightarrow {AM} {\rm{ \;}} + \overrightarrow {NA} {\rm{ \;}} + \overrightarrow {BQ} }\\{ = \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {BQ} {\rm{ \;}} + \overrightarrow {NA} }\\{ = \overrightarrow {MQ} {\rm{ \;}} + \overrightarrow {NA} }\\{ = \overrightarrow {BN} {\rm{ \;}} + \overrightarrow {NA} }\\{ = \overrightarrow {BA} }\end{array}\)
Chọn B.
Câu 4 (NB):
Phương pháp:
Sử dụng định lí cosin trong tam giác: \(B{C^2} = A{B^2} + A{C^2} – 2AB.AC.\cos \angle BAC.\)
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{B{C^2} = A{B^2} + A{C^2} – 2AB.AC.\cos \angle BAC.}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {6^2} + {8^2} – 2.6.8.\cos {{120}^0}}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = 148}\\{ \Rightarrow BC = \sqrt {148} {\rm{ \;}} = 2\sqrt {37} .}\end{array}\)
Chọn D.
Câu 5 (NB):
Phương pháp:
Cặp số nào thỏa mãn bất phương trình là nghiệm của bất phương trình.
Cách giải:
Thay cặp số (x;y) = (0;4) vào bất phương trình: 0 – 4 + 3 > 0 => Sai.
Thay cặp số (x;y) = (2;5) vào bất phương trình: 2 – 5 + 3 > 0 => Sai.
Thay cặp số (x;y) = (1;3) vào bất phương trình: 1 – 3 + 3 > 0 => Đúng.
Thay cặp số (x;y) = (1;4) vào bất phương trình: 1 – 4 + 3 > 0 => Sai.
Chọn C.
Câu 6 (TH):
Phương pháp:
Sử dụng quy tắc hình bình hành.
Cách giải:
Theo quy tắc hình bình hành ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AD} {\rm{ \;}} = \overrightarrow {AC} }\\{ \Rightarrow \overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} {\rm{ \;}} + \overrightarrow {AD} {\rm{ \;}} = \overrightarrow {AC} {\rm{ \;}} + \overrightarrow {AC} {\rm{ \;}} = 2\overrightarrow {AC} }\\{ \Rightarrow k = 2.}\end{array}\)
Chọn C.
Câu 7 (NB):
Phương pháp:
Sử dụng các công thức tính diện tích tam giác: \(S = \frac{{abc}}{{4R}}\), \(S = \frac{1}{2}ab\sin C\), \(S = \frac{1}{2}\sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} \), \(S = p.R\) với \(p = \frac{{a + b + c}}{2}.\)
Cách giải:
\(S = \frac{1}{2}ab\sin C\) nên đáp án D sai.
Chọn D.
Câu 8 (VD):
Phương pháp:
Sử đụng hằng đẳng thức để biến đổi biểu thức đề bài cho.
Sử dụng hệ quả định lí cosin trong tam giác.
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{{a^4} + {b^4} + {c^4} + {a^2}{c^2} – 2{a^2}{b^2} – 2{b^2}{c^2} = 0}\\{ \Leftrightarrow {a^4} + {c^4} + 2{a^2}{c^2} – {a^2}{c^2} + {b^4} – 2{a^2}{b^2} – 2{b^2}{c^2} = 0.}\\{ \Leftrightarrow {{\left( {{a^2} + {c^2}} \right)}^2} – 2{b^2}\left( {{a^2} + {c^2}} \right) + {b^4} – {a^2}{c^2} = 0}\\{ \Leftrightarrow {{\left( {{a^2} + {c^2} – {b^2}} \right)}^2} = {{\left( {ac} \right)}^2}}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{a^2} + {c^2} – {b^2} = ac}\\{{a^2} + {c^2} – {b^2} = – ac}\end{array}} \right.}\end{array}\)
Áp dụng hệ quả định lí cosin trong tam giác ta có: \(\cos B = \frac{{{a^2} + {c^2} – {b^2}}}{{2ac}} \Rightarrow {a^2} + {c^2} – {b^2} = 2ac\cos B\).
\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{2ac\cos B = ac}\\{2ac\cos B = {\rm{ \;}} – ac}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\cos B = \frac{1}{2}}\\{\cos B = {\rm{ \;}} – \frac{1}{2}}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{B = {{60}^0}}\\{B = {{120}^0}}\end{array}} \right.\).
Chọn D.
Câu 9 (TH):
Phương pháp:
Biểu diễn các tập hợp trên trục số và thực hiện các phép toán trên tập hợp.
Cách giải:

\(P\backslash Q = \left[ { – 4; – 3} \right] \Rightarrow A\) đúng.
\(P \cap Q = \left( { – 3;5} \right) \Rightarrow B\) sai.
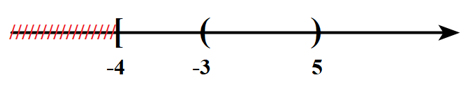
\(P \cup Q = \left[ { – 4; + \infty } \right) \Rightarrow C\) sai.
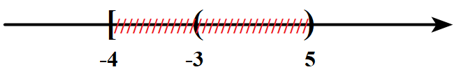
\({C_\mathbb{R}}P = \mathbb{R}\backslash P = \left( { – \infty ; – 4} \right) \cup \left[ {5; + \infty } \right) \Rightarrow D\) sai.
Chọn A.
Câu 10 (TH):
Phương pháp:
Sử dụng khái niệm các phép toán trên tập hợp.
Cách giải:
Phần tô đậm trong hình vẽ biểu diễn cho tập hợp \(\left( {A \cap B} \right)\backslash C.\)
Chọn D.
Câu 11 (TH):
Phương pháp:
Sử dụng định lí Cosin trong tam giác ABC ta có: \(A{B^2} = A{C^2} + B{C^2} – 2AC.BC.\cos C.\)
Cách giải:
Áp dụng định lí Cosin trong tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{A{B^2} = A{C^2} + B{C^2} – 2AC.BC.\cos C}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {{200}^2} + {{180}^2} – 2.200.180.\cos {{52}^0}16′ \approx 28337}\\{ \Rightarrow AB \approx 168{\mkern 1mu} {\mkern 1mu} \left( m \right)}\end{array}\)
Chọn D.
Câu 12 (TH):
Phương pháp:
Dùng công thức \({\sin ^2}x + {\cos ^2}x = 1\) để tính cos x
Cách giải:
\(\begin{array}{*{20}{l}}{\sin x = \frac{1}{2} \Rightarrow \sin {x^2} = \frac{1}{4} \Rightarrow {{\cos }^2}x = 1 – {{\sin }^2}x = 1 – \frac{1}{4} = \frac{3}{4}}\\{ \Rightarrow {{\sin }^2}x – {{\cos }^2}x = \frac{1}{4} – \frac{3}{4} = \frac{{ – 1}}{2}}\end{array}\)
Chọn B.
Câu 13 (TH):
Phương pháp:
Xác định tập hợp A, B dưới dạng khoảng, đoạn, nửa khoảng.
Biểu diễn và tìm giao trên trục số.
Cách giải:
\(\begin{array}{*{20}{l}}{A = \left\{ {x \in \mathbb{R}| – 1 < x < 4} \right\} \Rightarrow A = \left( { – 1;4} \right).}\\{B = \left\{ {x \in \mathbb{R}|\left| x \right| \le 3} \right\} \Rightarrow B = \left[ { – 3;3} \right].}\end{array}\)
Vậy \(A \cap B = \left( { – 1;3} \right].\)
Chọn B.
Câu 14 (TH):
Phương pháp:
Nếu \(\alpha {\rm{ \;}} + \beta {\rm{ \;}} = {90^0}\) thì \(\sin \alpha {\rm{ \;}} = \cos \beta \).
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{A = {{\sin }^2}{{51}^0} + {{\sin }^2}{{55}^0} + {{\sin }^2}{{39}^0} + {{\sin }^2}{{35}^0}}\\{A = \left( {{{\sin }^2}51 + {{\sin }^2}{{39}^0}} \right) + \left( {{{\sin }^2}{{55}^0} + {{\sin }^2}{{35}^0}} \right)}\\{A = \left( {{{\sin }^2}51 + {{\sin }^2}\left( {{{90}^0} – {{51}^0}} \right)} \right) + \left( {{{\sin }^2}{{55}^0} + {{\sin }^2}\left( {{{90}^0} – {{55}^0}} \right)} \right)}\\{A = \left( {{{\sin }^2}51 + {{\cos }^2}{{51}^0}} \right) + \left( {{{\sin }^2}{{55}^0} + {{\cos }^2}{{55}^0}} \right)}\\{A = 1 + 1 = 2.}\end{array}\)
Chọn D.
Câu 15 (TH):
Phương pháp:
Vì M đứng yên nên \(\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} {\rm{ \;}} + \overrightarrow {{F_3}} {\rm{ \;}} = \vec 0{\rm{ \;}} \Rightarrow \overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\).
Sử dụng quy tắc hình bình hành.
Cách giải:
Vì M đứng yên nên \(\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} {\rm{ \;}} + \overrightarrow {{F_3}} {\rm{ \;}} = \vec 0{\rm{ \;}} \Rightarrow \overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\).
Áp dụng quy tắc hình bình hành ta có: \(\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} = \overrightarrow {MD} \), với D là đỉnh thứ tư của hình bình hành AMBD như hình vẽ.
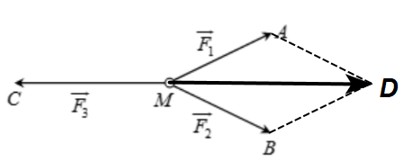
\(\begin{array}{*{20}{l}}{ \Rightarrow \overrightarrow {MD} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0{\rm{ \;}} \Rightarrow \overrightarrow {MC} {\rm{ \;}} = {\rm{ \;}} – \overrightarrow {MD} }\\{ \Rightarrow \left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {MC} } \right| = \left| { – \overrightarrow {MD} } \right| = MD}\end{array}\)
Vì MA = MB = 100, \(\angle AMB = {60^0}\) nên tam giác AMB đều \( \Rightarrow MD = 100\sqrt 3 \).
Vậy \(\left| {\overrightarrow {{F_3}} } \right| = 100\sqrt 3 N.\)
Chọn D.
Câu 16 (TH):
Phương pháp:
Dựa vào các khái niệm về hai vectơ cùng phương, cùng hướng.
Cách giải:
Dễ thấy A, B đúng.
C: \(\vec a,{\mkern 1mu} {\mkern 1mu} \vec b\) cùng phương với \(\vec c\) nên giá của \(\vec a,{\mkern 1mu} {\mkern 1mu} \vec b\) song song hoặc trùng với giá của \(\vec c\) => Giá của \(\vec a,{\mkern 1mu} {\mkern 1mu} \vec b\) song song hoặc trùng nhau, do đó \(\vec a,{\mkern 1mu} {\mkern 1mu} \vec b\) cùng phương => C đúng.
Chọn D.
Câu 17 (VD):
Phương pháp:
Xác định và so sánh phương sai, độ lệch chuẩn về tốc độ của 20 chiếc xe ô tô trên mỗi con đường.
Cách giải:
*) Con đường A
Bảng phân bố tần số:

Số trung bình: \(\overline {{x_A}} {\rm{\;}} = \frac{{60.2 + 65.4 + 68.2 + 72.1 + 75.2 + 76.2 + 80.2 + 84.1 + 85.2 + 90.2}}{{20}}\)\( = 74,2\left( {{\rm{km/h}}} \right)\)
Phương sai: \(s_A^2 = \frac{1}{{20}}\left[ {2.{{(60 – 74,2)}^2} + 4.{{(65 – 74,2)}^2} + … + 2.{{(90 – 74,2)}^2}} \right] = 86,36\left( {km/h} \right)\)
Độ lệch chuẩn: \({s_A} = \sqrt {s_A^2} {\rm{\;}} = \sqrt {86,36} {\rm{\;}} \approx 9,29{\mkern 1mu} {\mkern 1mu} \left( {km/h} \right)\)
*) Con đường B
Bảng phân bố tần số:

Số trung bình: \({x_B} = \frac{{55.3 + 60.1 + 62.2 + 64.2 + 70.3 + 76.2 + 79.3 + 80.2 + 85.2}}{{20}} = 70,3\left( {{\rm{km/h}}} \right)\)
Phương sai: \(s_B^2 = \frac{1}{{20}}\left[ {3.{{(55 – 70,3)}^2} + 1.{{(60 – 70,3)}^2} + … + 2.{{(85 – 70,3)}^2}} \right] = 96,91\left( {km/h} \right)\)
Độ lệch chuẩn: \({s_B} = \sqrt {s_B^2} {\rm{\;}} = \sqrt {96,91} {\rm{\;}} \approx 9,84{\mkern 1mu} {\mkern 1mu} \left( {km/h} \right)\)
Vậy xe chạy trên con đường A sẽ an toàn hơn.
Chọn A.
Câu 18 (NB):
Phương pháp:
Cho mẫu số liệu có kích thước \(N\) là \(\left\{ {{x_1};{\mkern 1mu} {\mkern 1mu} {x_2};{\mkern 1mu} {\mkern 1mu} \ldots ;{\mkern 1mu} {\mkern 1mu} {x_N}} \right\}\). Phương sai của mẫu số liệu này bằng trung bình của tổng các bình phương độ lệch giữa các giá trị với số trung bình.
Cách giải:
Dựa theo lý thuyết, ta có:
Dãy số liệu \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2}, \ldots ,{\mkern 1mu} {\mkern 1mu} {x_N}\) có kích thước mẫu \(N\), phương sai được tính theo công thức:
\({s^2} = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{x_i} – \bar x} \right)}^2}} \) trong đó \(\bar x = \) trung bình cộng của mẫu số liệu
Chọn A.
Câu 19 (TH):
Phương pháp:
Sử dụng công thức: \(\overrightarrow {BA} .\overrightarrow {BC} {\rm{ \;}} = BA.BC.\cos \angle \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right).\)
Cách giải:
Vì ABC là tam giác vuông cân tại A nên \(BC = AB\sqrt 2 {\rm{ \;}} = 4\sqrt 2 \) và \(\left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = \angle ABC = {45^0}\).
Vậy \(\overrightarrow {BA} .\overrightarrow {BC} {\rm{ \;}} = BA.BC.\cos \angle \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right)\)
\( = 4.4\sqrt 2 .\cos {45^0} = 4.4\sqrt 2 .\frac{{\sqrt 2 }}{2} = 16.\)
Chọn B.
Câu 20 (TH):
Phương pháp:
Đối với bảng phân bố tần số ghép lớp:
+ Số trung bình cộng: \(\bar x = \frac{{{c_1}{n_1} + {c_2}{n_2} + \ldots + {c_k}{n_k}}}{N}\)
+ Phương sai: \({s^2} = \frac{1}{N}\left[ {{n_1}{{\left( {{c_1} – \bar x} \right)}^2} + {n_2}{{\left( {{c_2} – \bar x} \right)}^2} + \ldots + {n_k}{{\left( {{c_k} – \bar x} \right)}^2}} \right]\)
+ Độ lệch chuẩn: \(s = \sqrt {{s^2}} \)
Với \({n_i}\) là tần số của giá trị \({c_i}\).
Cách giải:
Ta có bảng phân bố tần số, tần suất ghép lớp:
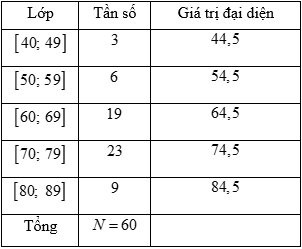
Số trung bình cộng:
\(\bar x = \frac{{44,5.3 + 54,5.6 + 64,5.19 + 74,5.23 + 84,5.9}}{{60}} = \frac{{4160}}{{60}} \approx 69,33\) (nghìn đồng)
Phương sai:
\({s^2} = \frac{1}{{60}}\left( {3.44,{5^2} + 6.54,{5^2} + 19.64,{5^2} + 23.74,{5^2} + 9.84,{5^2}} \right) – {\left( {\frac{{4160}}{{60}}} \right)^2}\)\( = \frac{{3779}}{{36}}\) (nghìn đồng)
Độ lệch chuẩn: \(s = \sqrt {{s^2}} \)\( = \sqrt {\frac{{3779}}{{36}}} {\rm{\;}} \approx 10,25\) (nghìn đồng)
Chọn B.
Câu 21 (NB):
Phương pháp:
Chọn điểm bất kì thỏa mãn bất phương trình để chọn miền nghiệm
Cách giải:
Vì O(0,0) không thuộc miền nghiệm nên nửa mặt phẳng có bờ là d khác phía gốc tọa độ O và không lấy đường thẳng d
Chọn D.
Câu 22 (NB):
Phương pháp:
Vẽ đồ thị hoặc thử các đáp án
Cách giải:
\(\left( {0,2} \right)\) thỏa mãn 3 phương trình trong hệ phương trình nên chọn D
Chọn D.
Câu 23 (TH):
Phương pháp:
Sử dụng định lí Sin trong tam giác \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\).
Cách giải:
Sử dụng định lí Sin trong tam giác \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\) \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2R\sin A}\\{b = 2R\sin B}\\{c = 2R\sin C}\end{array}} \right.\).
Theo giả thiết ta có:
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} b + c = 2a}\\{ \Leftrightarrow 2R\sin B + 2R\sin C = 2.2R\sin A}\\{ \Leftrightarrow \sin B + \sin C = 2\sin A.}\end{array}\)
Chọn B.
Câu 24 (TH):
Phương pháp:
Sử dụng công thức \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = BM.BA.\cos \left( {\overrightarrow {BM} ,\overrightarrow {BA} } \right).\)
Cách giải:
Ta có: \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} – \frac{1}{2}\overrightarrow {BC} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} – \frac{1}{2}BC.BA.\cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right).\)
Vì tam giác ABC đều nên \(\cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right) = \angle ABC = {60^0}\).
\( \Rightarrow \overrightarrow {BM} .\overrightarrow {BA} = – \frac{1}{2}.4.4.\frac{{\sqrt 3 }}{2} = {\rm{ \;}} – 4\sqrt 3 .\)
Chọn B.
Câu 25 (NB):
Phương pháp:
Xác định số gần đúng a và độ chính xác d.
Tính số đúng \(\bar a = a \pm d \Rightarrow a – d \le \bar a \le a + d\).
Cách giải:
Gọi \(\bar a\) là chiều dài đúng của dây cầu \( \Rightarrow \bar a = 152m \pm 0,2m\).
\(\begin{array}{*{20}{l}}{ \Rightarrow 152 – 0,2 \le \bar a \le 152 + 0,2}\\{ \Leftrightarrow 151,8 \le \bar a \le 152,2}\end{array}\)
Vậy chiều dài đúng của cây cầu là một số nằm trong khoảng 151,8m đến 152,2m.
Chọn A.
Câu 26 (TH):
Phương pháp:
Đổi sang đơn vị m.
Tính diện tích hình chữ nhật bằng dài nhân rộng.
Cách giải:
Diện tích hình chữ nhật là
\(\begin{array}{*{20}{l}}{\left( {2 \pm 0,01} \right)\left( {5 \pm 0,02} \right)}\\{ = 10 \pm \left( {0,04 + 0,05 + 0,01.0,02} \right)}\\{ = 10 \pm 0,0902}\end{array}\)
=> diện tích hình chữ nhật là \(\bar S = \)10m2, độ chính xác là d = 0,0902m2
=> Sai số tuyệt đối: \(\Delta {\rm{ \;}} \le 0,0902{\mkern 1mu} {\mkern 1mu} \left( {{m^2}} \right) = 902{\mkern 1mu} {\mkern 1mu} \left( {c{m^2}} \right)\).
Vậy diện tích hình chữ nhật là 10m2 và sai số tuyệt đối là 900cm2.
Chọn C.
Câu 27 (TH):
Phương pháp:
Khoảng biến thiên, kí hiệu là R, là hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất trong mẫu số liệu.
Cách giải:
Giá trị lớn nhất trong mẫu số liệu là 19.
Giá trị nhỏ nhất trong mẫu số liệu là 2.
Vậy khoảng biến thiên R = 19 – 2 = 17.
Chọn C.
Câu 28 (VD):
Phương pháp:
Sử dụng công thức \(n\left( {A \cup B \cup C} \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) – n\left( {A \cap B} \right) – n\left( {B \cap C} \right) – n\left( {C \cap A} \right) + n\left( {A \cap B \cap C} \right)\).
Cách giải:
Gọi A là tập hợp các bạn đăng kí tiết mục tốp ca \( \Rightarrow n\left( A \right) = 7.\)
B là tập hợp các bạn đăng kí tiết mục múa \( \Rightarrow n\left( B \right) = 6.\)
C là tập hợp các bạn đăng kí tiết mục diễn kịch \( \Rightarrow n\left( C \right) = 8.\)
\( \Rightarrow A \cap B:\) tập hợp các bạn đăng kí cả 2 tiết mục tốp ca và múa \( \Rightarrow n\left( {A \cap B} \right) = 3.\)
\(A \cap C\): tập hợp các bạn đăng kí cả 2 tiết mục tốp ca và diễn kịch \( \Rightarrow n\left( {A \cap C} \right) = 4.\)
\(B \cap C\): tập hợp các bạn đăng kí cả 2 tiết mục múa và diễn kịch \( \Rightarrow n\left( {B \cap C} \right) = 2.\)
\(A \cap B \cap C\): tập hợp các bạn đăng kí cả 3 tiết mục tốp ca, múa và diễn kịch \( \Rightarrow n\left( {A \cap B \cap C} \right) = 1.\)
\(A \cup B \cup C\): tập hợp các bạn đăng kí ít nhất 1 tiết mục.
Ta có: \(n\left( {A \cup B \cup C} \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) – n\left( {A \cap B} \right) – n\left( {B \cap C} \right) – n\left( {C \cap A} \right) + n\left( {A \cap B \cap C} \right)\)
\( \Rightarrow n\left( {A \cup B \cup C} \right) = 7 + 6 + 8 – 3 – 4 – 2 + 1 = 13.\)
Chọn B.
Câu 29 (TH):
Phương pháp:
Sử dụng hai vectơ bằng nhau, đưa về hai vectơ chung điểm đầu và cuối, sử dụng quy tắc ba điểm.
Cách giải:
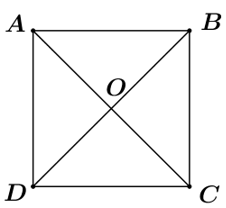
Ta có: \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {OD} {\rm{ \;}} = \overrightarrow {OD} {\rm{ \;}} + \overrightarrow {AB} {\rm{ \;}} = \overrightarrow {OD} {\rm{ \;}} + \overrightarrow {DC} {\rm{ \;}} = \overrightarrow {OC} \).
\( \Rightarrow \left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {OD} } \right| = \left| {\overrightarrow {OC} } \right| = OC\).
Áp dụng định lí Pytago ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} {\rm{ \;}} = \sqrt {{{\left( {4a} \right)}^2} + {{\left( {3a} \right)}^2}} {\rm{ \;}} = 5a \Rightarrow OC = \frac{1}{2}AC = \frac{5}{2}a.\)
Vậy \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {OD} } \right| = OC = \frac{5}{2}a.\)
Chọn C.
Câu 30 (TH):
Phương pháp:
Sử dụng định nghĩa tích vô hướng của hai vectơ: \(\vec a.\vec b{\rm{ \;}} = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\).
Cách giải:
Ta có:
\(\begin{array}{l}\vec a.\vec b = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\\ \Leftrightarrow 2\vec a.\vec b = 2\left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\\ \Leftrightarrow – \left| {\vec a} \right|.\left| {\vec b} \right| = 2\left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\\ \Leftrightarrow \left| {\vec a} \right|.\left| {\vec b} \right|\left[ {1 + 2\cos \left( {\vec a,\vec b} \right)} \right] = 0\\ \Leftrightarrow \cos \left( {\vec a,\vec b} \right) = – \frac{1}{2}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} \vec a \ne \vec 0,{\mkern 1mu} {\mkern 1mu} \vec b \ne \vec 0} \right)\end{array}\)
\( \Leftrightarrow \left( {\vec a,\vec b} \right) = {120^0}.\)
Chọn B.
Phần 2: Tự luận (4 điểm)
Câu 1 (VD):
Phương pháp:
a) Gọi I là trung điểm của BC. Chứng minh M là trung điểm của BI.
Sử dụng quy tắc ba điểm, công thức trung điểm.
b) Sử dụng điều kiện để hai vectơ cùng phương.
Cách giải:
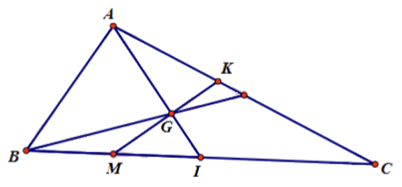
a) Gọi I là trung điểm của BC.
Ta có: \(3\overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0{\rm{ \;}} \Rightarrow 3MB = MC \Rightarrow MB = \frac{1}{4}BC = \frac{1}{2}BI\).
=> M là trung điểm của BI.
Khi đó ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {MG} = \overrightarrow {MI} + \overrightarrow {IG} = \frac{1}{4}\overrightarrow {BC} – \frac{1}{3}\overrightarrow {AI} }\\{ = \frac{1}{4}\left( {\overrightarrow {AC} – \overrightarrow {AB} } \right) – \frac{1}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)}\\{ = \frac{1}{4}\overrightarrow {AC} – \frac{1}{4}\overrightarrow {AB} – \frac{1}{6}\overrightarrow {AB} – \frac{1}{6}\overrightarrow {AC} }\\{ = \frac{1}{{12}}\overrightarrow {AC} – \frac{5}{{12}}\overrightarrow {AB} {\mkern 1mu} {\mkern 1mu} \left( {dpcm} \right).}\end{array}\)
b) Đặt \(\overrightarrow {AK} {\rm{ \;}} = x\overrightarrow {AC} {\mkern 1mu} {\mkern 1mu} \left( {x > 0} \right)\), ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {GK} {\rm{ \;}} = \overrightarrow {AK} {\rm{ \;}} – \overrightarrow {AG} {\rm{ \;}} = x\overrightarrow {AC} {\rm{ \;}} – \frac{2}{3}\overrightarrow {AI} }\\{ = x\overrightarrow {AC} {\rm{ \;}} – \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right) = \left( {x – \frac{1}{3}} \right)\overrightarrow {AC} {\rm{ \;}} – \frac{1}{3}\overrightarrow {AB} }\end{array}\)
Vì M, G, K thẳng hàng nên \(\frac{{x – \frac{1}{3}}}{{\frac{1}{{12}}}} = \frac{{ – \frac{1}{3}}}{{ – \frac{5}{{12}}}} \Leftrightarrow x = \frac{2}{5}.\)
Vậy \(\overrightarrow {AK} {\rm{\;}} = \frac{2}{5}\overrightarrow {AC} \) nên \(AK = \frac{2}{5}AC \Rightarrow \frac{{KA}}{{KC}} = \frac{2}{3}.\)
Câu 2 (VD):
Phương pháp:
a)
* Số trung bình của mẫu số liệu \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2},{\mkern 1mu} {\mkern 1mu} ….,{\mkern 1mu} {\mkern 1mu} {x_n}\) kí hiệu là \(\bar x\), được tính bằng công thức:
\(\bar x = \frac{{{x_2} + {x_2} + … + {x_k}}}{n}\)
* Tìm trung vị của mẫu số liệu.
Để tìm trung vị của mẫu số liệu, ta thực hiện như sau:
– Sắp xếp các giá trị trong mẫu số liệu theo thứ tự không giảm.
– Nếu giá trị của mẫu số liệu là số lẻ thì giá trị chính giữa của mẫu là trung vị. Nếu là số chẵn thì trung vị là trung bình cộng của hai giá trị chính giữa của mẫu.
b) So sánh và kết luận.
Cách giải:
a)
* Số trung bình của dãy số trên là:
\(\bar x{\rm{ \;}} = \frac{{\begin{array}{*{20}{l}}{190174 + 81182 + 19728 + 19048 + 8155 + 6103 + 5807 + }\\{4544 + 3760 + 3297 + 2541 + 2000 + 1934 + 1602 + 1195}\end{array}}}{{15}} \approx 23{\mkern 1mu} 404,67\).
* Sắp xếp dãy số liệu theo thứ tự không giảm ta được:
1 195 1 602 1 934 2 000 2 541 3 297 3 760 4 544
5 807 6 103 8 155 19 048 19 728 81 182 190 174
Cỡ mẫu là n = 15 lẻ nên số trung vị là \({M_e} = 4{\mkern 1mu} 544\).
b) Số trung bình lớn hơn nhiều so với số trung vị là do trong dãy số có một giá trị rất lớn là 190 174. Trung vị không bị ảnh hưởng bởi giá trị “bất thường” này.
Câu 3 (VDC):
Phương pháp:
Ta thường dùng các chữ cái in hoa để kí hiệu tập hợp và chữ cái in thường để kí hiệu phần tử thuộc tập hợp.
Cách giải:
Ta có
\(\begin{array}{l}S = G{B^2} + G{C^2} + 9G{A^2}\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\left( {\frac{2}{3}{m_b}} \right)^2} + {\left( {\frac{2}{3}{m_c}} \right)^2} + 9.{\left( {\frac{2}{3}{m_a}} \right)^2}\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{4}{9}{m_b}^2 + \frac{4}{9}{m_c}^2 + 4{m_a}^2\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{4}{9}.\left( {\frac{{2{a^2} + 2{c^2} – {b^2}}}{4} + \frac{{2{a^2} + 2{b^2} – {c^2}}}{4}} \right) + 4.\frac{{2{b^2} + 2{c^2} – {a^2}}}{4}\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{4}{9}.\frac{{4{a^2} + {b^2} + {c^2}}}{4} + 2{b^2} + 2{c^2} – {a^2}\end{array}\)
\(\begin{array}{l}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{{4{a^2} + {b^2} + {c^2}}}{9} + 2{b^2} + 2{c^2} – {a^2}\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{{19}}{9}\left( {{b^2} + {c^2}} \right) – \frac{5}{9}{a^2}\end{array}\)
Theo giả thiết ta có: \(4\sin A\tan A = \sin B\sin C \Leftrightarrow 4{\sin ^2}A = \sin B\sin C\cos A{\mkern 1mu} {\mkern 1mu} \left( * \right)\)
Áp dụng định lí sin trong tam giác ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\sin A = \frac{a}{{2R}}}\\{\sin B = \frac{b}{{2R}}}\\{\sin C = \frac{c}{{2R}}}\end{array}} \right.\)
Thay vào (*) ta có:
\(\begin{array}{*{20}{l}}{\left( * \right) \Leftrightarrow 4{{\left( {\frac{a}{{2R}}} \right)}^2} = \frac{b}{{2R}}.\frac{c}{{2R}}\cos A}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \Leftrightarrow 4.\frac{{{a^2}}}{{4{R^2}}} = \frac{{bc}}{{4{R^2}}}\cos A}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \Leftrightarrow 4{a^2} = bc\cos A}\end{array}\)
Lại theo định lí cosin trong tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{{a^2} = {b^2} + {c^2} – 2bc\cos A}\\{ \Rightarrow bc\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{2}}\end{array}\)
Khi đó ta có:
\(\begin{array}{*{20}{l}}{\left( * \right) \Leftrightarrow 4{a^2} = \frac{{{b^2} + {c^2} – {a^2}}}{2}}\\{ \Leftrightarrow 8{a^2} = {b^2} + {c^2} – {a^2}}\\{ \Leftrightarrow 9{a^2} = {b^2} + {c^2}}\end{array}\)
Do đó: \(S = \frac{{19}}{9}\left( {{b^2} + {c^2}} \right) – \frac{5}{9}{a^2} = \frac{{19}}{9}.9{a^2} – \frac{5}{9}{a^2} = \frac{{166{a^2}}}{9} = 166.\)
Vậy S = 166.
Đề 2
I. Trắc nghiệm (7 điểm)
Câu 1: Cho các câu sau:
(1) Số 7 là số lẻ.
(2) Bài toán này khó quá!
(3) Cuối tuần này bạn có rảnh không?
(4) Số 10 là một số nguyên tố.
Trong các câu trên có bao nhiêu câu là mệnh đề?
A. 1. B. 2. C. 3. D. 4.
Câu 2: Mệnh đề phủ định của mệnh đề “\(\forall x \in \mathbb{R},\,\,x – 2 > 5\)” là:
A. “\(\exists x \in \mathbb{R},\,\,x – 2 \le 5\)”. B. “\(\exists x \in \mathbb{R},\,\,x – 2 \ge 5\)”. C. “\(\forall x \in \mathbb{R},\,\,x – 2 \le 5\)”. D. “\(\forall x \in \mathbb{R},\,\,x – 2 \ge 5\)”.
Câu 3: Cho tập hợp \(D = \left\{ {x \in {\mathbb{N}^*}|x\left( {x – 2} \right)\left( {x – 3} \right) = 0} \right\}\). Viết lại tập hợp D dưới dạng liệt kê các phần tử của tập hợp đó.
A. D = {2;3}. B. D = {0;1;2}. C. D = {1;2}. D. D = {0;2;3}.
Câu 4: Xác định tập hợp B = {3;6;9;12;15} bằng cách nêu tính chất đặc trưng cho các phần tử của tập hợp.
A. \(B = \left\{ {3n|n \in \mathbb{N},\,\,1 \le n \le 5} \right\}\). B. \(B = \left\{ {n|n\,\, \vdots \,\,3} \right\}\).
C. \(B = \left\{ {3n|n \in \mathbb{N},\,\,1 < n < 5} \right\}\). D. \(B = \left\{ {n|n \in \mathbb{N},\,\,0 \le n \le 5} \right\}\).
Câu 5: Cho hai tập hợp \(A = \left( { – \infty ; – 2} \right]\) và \(B = \left( { – 3;5} \right]\). Tìm mệnh đề sai.
A. \(A \cap B = \left( { – 3; – 2} \right].\) B. \(A\backslash B = \left( { – \infty ; – 3} \right)\). C. \(A \cup B = \left( { – \infty ;5} \right]\). D. \(B\backslash A = \left( { – 2;5} \right]\).
Câu 6: Trong các tập hợp sau, tập hợp nào là tập con của tập hợp \(A = \left\{ {1;2;3;4;5} \right\}\)?
A. \({A_1} = \left\{ {1;6} \right\}.\) B. \({A_2} = \left\{ {0;1;3} \right\}.\) C. \({A_3} = \left\{ {4;5} \right\}.\) D. \({A_4} = \left\{ 0 \right\}.\)
Câu 7: Trong các mệnh đề dưới đây, mệnh đề nào đúng?
A. 12 là số nguyên tố. B. 9 là số nguyên tố. C. 4 là số nguyên tố. D. 5 là số nguyên tố.
Câu 8: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. \(2{x^3} + 1 \ge y + 2{x^2}.\) B. \(2x – 6y + 5 < 2x – 6y + 3.\)
C. \(2{x^2} + 1 \ge y + 2{x^2}.\) D. \(4{x^2} < 2x + 5y – 6.\)
Câu 9: Điểm nào dưới đây thuộc miền nghiệm của bất phương trình \(3x + 2y < 10\)?
A. (5;1). B. (4;2). C. (1;5). D. (1;2).
Câu 10: Trong tam giác EFG, chọn mệnh đề đúng.
A. \(E{F^2} = E{G^2} + F{G^2} + 2EG.FG.\cos G.\) B. \(E{F^2} = E{G^2} + F{G^2} + 2EG.FG.\cos E.\)
C. \(E{F^2} = E{G^2} + F{G^2} – 2EG.FG.\cos E.\) D. \(E{F^2} = E{G^2} + F{G^2} – 2EG.FG.\cos G.\)
Câu 11: Cho tam giác ABC biết \(\frac{{\sin B}}{{\sin C}} = \sqrt 3 \) và \(AB = 2\sqrt 2 \). Tính AC.
A. \(2\sqrt 3 .\) B. \(2\sqrt 5 .\) C. \(2\sqrt 2 .\) D. \(2\sqrt 6 .\)
Câu 12: Cho tam giác ABC có b = 7, c = 5, \(\cos A = \frac{3}{5}.\) Độ dài đường cao \({h_a}\) của tam giác ABC là:
A. \(8.\) B. \(8\sqrt 3 .\) C. \(\frac{{7\sqrt 2 }}{2}.\) D. \(7\sqrt 2 .\)
Câu 13: Với giá trị nào của x sau đây, mệnh đề chứa biến P(x): “\({x^2} – 5x + 4 = 0\)” là mệnh đề đúng?
A. 0. B. \(\frac{4}{5}\). C. 5. D. 1.
Câu 14: Trong các hệ bất phương trình sau, hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?
A. \(\left\{ \begin{array}{l}{x^2} – 4 \ge 0\\3x + 4y < 2\end{array} \right.\). B. \(x – y > 0\). C. \(\left\{ \begin{array}{l}{y^2} + 2y – 3 > 0\\5x – y > 2\end{array} \right.\). D. \(\left\{ \begin{array}{l}x – 4 \ge y\\3x + 4y < 5\end{array} \right.\).
Câu 15: Giá trị của biểu thức \(T = 2 + {\sin ^2}{90^0} + 2{\cos ^2}{60^0} – 3{\tan ^2}{45^0}\) bằng:
A. 3. B. \( – \frac{1}{2}\). C. 1. D. \(\frac{1}{2}\).
Câu 16: Cho tam giác ABC có BC = a, AC = b, AB = c, có R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp và hc là độ dài đường cao xuất phát từ đỉnh C. Chọn mệnh đề sai.
A. \({S_{ABC}} = ab\sin C.\) B. \({S_{ABC}} = pr.\) C. \({S_{ABC}} = \frac{{abc}}{{4R}}.\) D. \({S_{ABC}} = \frac{1}{2}c.{h_c}.\)
Câu 17: Tam giác ABC có BC = 1, AC = 3, \(\angle C = {60^0}\). Tính độ dài cạnh AB.
A. \(\sqrt {13} .\) B. \(\sqrt 7 .\) C. \(\frac{{\sqrt {34} }}{2}.\) D. \(\frac{{\sqrt {46} }}{2}.\)
Câu 18: Cho mệnh đề: “Nếu tứ giác là một hình thoi thì tứ giác đó nội tiếp được một đường tròn”. Mệnh đề đảo của mệnh đề trên là:
A. “Tứ giác là một hình thoi khi và chỉ khi tứ giác đó nội tiếp được trong một đường tròn”.
B. “Tứ giác là một hình thoi kéo theo tứ giác đó nội tiếp được trong một đường tròn”.
C. “Một tứ giác nội tiếp được trong một đường tròn khi và chỉ khi tứ giác đó là hình thoi”.
D. “Nếu một tứ giác nội tiếp được trong một đường tròn thì tứ giác đó là hình thoi”.
Câu 19: Phần không bị gạch trên hình vẽ dưới đây minh họa cho tập hợp nào?
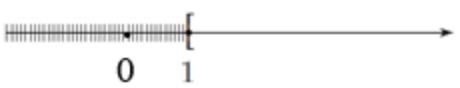
A. \(\left( {0;1} \right).\) B. \(\left( {1; + \infty } \right).\) C. \(\left[ {1; + \infty } \right).\) D. \(\left( {0;1} \right].\)
Câu 20: Cho \(\alpha \) và \(\beta \) là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?
A. \(\sin \alpha = \sin \beta .\) B. \(\cos \alpha = – \cos \beta .\) C. \(\tan \alpha = – \tan \beta .\) D. \(\cot \alpha = \cot \beta .\)
Câu 21: Cho hai tập hợp \(A = \left\{ {1;2;4;6} \right\}\) và \(B = \left\{ {1;2;3;4;5;6;7;8} \right\}\). Xác định tập hợp \({C_B}A\).
A. \({C_B}A = \left\{ {3;5;7;8} \right\}.\) B. \({C_B}A = \left\{ {4;6} \right\}.\) C. \({C_B}A = \left\{ {1;2;4;6} \right\}.\) D. \({C_B}A = \left\{ {2;6;7;8} \right\}.\)
Câu 22: Tam giác ABC có AB = 4, BC = 6, \(AC = 2\sqrt 7 \). Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM.
A. \(AM = 3\sqrt 2 .\) B. \(AM = 4\sqrt 2 .\) C. \(AM = 2\sqrt 3 .\) D. \(AM = 3.\)
Câu 23: Nửa mặt phẳng không bị gạch chéo ở hình dưới đây là miền nghiệm của bất phương trình nào trong các bất phương trình sau?

A. \(2x + y < 1.\) B. \(2x – y > 1.\) C. \(x + 2y > 1.\) D. \(2x + y > 1.\)
Câu 24: Cho góc \(\alpha \) với \({0^0} < \alpha < {180^0}\). Tính giá trị của \(\cos \alpha \), biết \(\tan \alpha = – 2\sqrt 2 \).
A. \( – \frac{1}{3}.\) B. \(\frac{1}{3}.\) C. \(\frac{{2\sqrt 2 }}{3}.\) D. \(\frac{{\sqrt 2 }}{3}.\)
Câu 25: Một ca nô xuất phát từ cảng A, chạy theo hướng đông với vận tốc 50 km/h. Cùng lúc đó, một tàu cá, xuất phát từ A, chạy theo hướng N30°E với vận tốc 40 km/h. Sau 3 giờ, hai tàu cách nhau bao nhiêu kilômét?
A. 135,7km. B. 237,5km. C. 110km. D. 137,5km.
Câu 26. Sử dụng máy tính bỏ túi, hãy viết giá trị gần đúng của \(\sqrt 3 \) chính xác đến hàng phần nghìn.
A. 1,7320. B. 1,732. C. 1,733. D. 1,731.
Câu 27. Đo độ cao một ngọn cây là \(h = 347,13{\rm{m}} \pm 0,2{\rm{m}}.\) Hãy viết số quy tròn của số gần đúng 347,13.
A. 345. B. 347. C. 348. D. 346.
Câu 28: Ba nhóm học sinh gồm 20 người, 15 người, 25 người. Cân nặng trung bình của mỗi nhóm lần lượt là 50kg, 38kg, 40kg. Cân nặng trung bình của cả ba nhóm học sinh là:
A. 41,6kg. B. 42,8kg. C. 41,8kg. D. Đáp số khác.
Câu 29: Có 100 học sinh dự thi học sinh giỏi Toán (điểm 20). Kết quả như sau:

Nhận xét nào sau đây là đúng?
A. Phương sai lớn hơn 4, độ lệch chuẩn lớn hơn 2
B. Phương sai lớn hơn 5, độ lệch chuẩn lớn hơn 2
C. Phương sai nhỏ hơn 5, độ lệch chuẩn lớn hơn 2
D. Phương sai nhỏ hơn 4, độ lệch chuẩn nhỏ hơn 2
Câu 30. Cho hình chữ nhật \(ABCD.\) Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AC} = \overrightarrow {BD} .\) B. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \vec 0.\)
C. \(\left| {\overrightarrow {AB} – \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} + \overrightarrow {AD} } \right|.\) D. \(\left| {\overrightarrow {BC} + \overrightarrow {BD} } \right| = \left| {\overrightarrow {AC} – \overrightarrow {AB} } \right|.\)
Câu 31. Cho tam giác \(ABC\) và điểm \(M\) thỏa mãn điều kiện \(\overrightarrow {MA} – \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \). Mệnh đề nào sau đây sai?
A. \(MABC\) là hình bình hành. B. \(\overrightarrow {AM} + \overrightarrow {AB} = \overrightarrow {AC} .\)
C. \(\overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BM} .\) D. \(\overrightarrow {MA} = \overrightarrow {BC} .\)
Câu 32. Cho hình bình hành ABCD. Đẳng thức nào sau đây đúng?
A.\(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {BC} \) B. \(\overrightarrow {AC} + \overrightarrow {BC} = \overrightarrow {AB} \)
C. \(\overrightarrow {AC} – \overrightarrow {BD} = 2\overrightarrow {CD} \) D. \(\overrightarrow {AC} – \overrightarrow {AD} = \overrightarrow {CD} \)
Câu 33. Cho tam giác OAB vuông cân tại O, cạnh \(OA = a\). Khẳng định nào sau đây sai?
A.\(\left| {3\overrightarrow {OA} + 4\overrightarrow {OB} } \right| = 5a\) B. \(\left| {2\overrightarrow {OA} } \right| + \left| {3\overrightarrow {OB} } \right| = 5a\)
C. \(\left| {7\overrightarrow {OA} – 2\overrightarrow {OB} } \right| = 5a\) D. \(\left| {11\overrightarrow {OA} } \right| – \left| {6\overrightarrow {OB} } \right| = 5a\)
Câu 34. Cho tam giác \(ABC\) có \(BC = a,\,{\rm{ }}CA = b,{\rm{ }}AB = c.\) Gọi \(M\) là trung điểm cạnh \(BC.\) Tính \(\overrightarrow {AM} .\overrightarrow {BC} .\)
A. \(\overrightarrow {AM} .\overrightarrow {BC} = \frac{{{b^2} – {c^2}}}{2}.\) B. \(\overrightarrow {AM} .\overrightarrow {BC} = \frac{{{c^2} + {b^2}}}{2}.\)
C. \(\overrightarrow {AM} .\overrightarrow {BC} = \frac{{{c^2} + {b^2} + {a^2}}}{3}.\) D. \(\overrightarrow {AM} .\overrightarrow {BC} = \frac{{{c^2} + {b^2} – {a^2}}}{2}.\)
Câu 35. Cho hình vuông \(ABCD\) cạnh \(a.\) Tính \(P = \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {BC} + \overrightarrow {BD} + \overrightarrow {BA} } \right).\)
A. \(P = 2\sqrt 2 a.\) B. \(P = 2{a^2}.\) C. \(P = {a^2}.\) D. \(P = – 2{a^2}.\)
II. Tự luận (3 điểm)
Câu 1: (1,5 điểm) Cho tam giác ABC, M là điểm bất kỳ.
a) Chứng minh rằng \(\overrightarrow {MA} .\overrightarrow {BC} + \overrightarrow {MB} .\overrightarrow {CA} + \overrightarrow {MC} .\overrightarrow {AB} = 0\)
b) Gọi G là trọng tâm tam giác ABC. Chứng minh: \(M{A^2} + M{B^2} + M{C^2} = 3M{G^2} + G{A^2} + G{B^2} + G{C^2}\)
c) Chứng minh rằng \(G{A^2} + G{B^2} + G{C^2} = \frac{1}{3}({a^2} + {b^2} + {c^2})\), với a, b, c là độ dài 3 cạnh của tam giác.
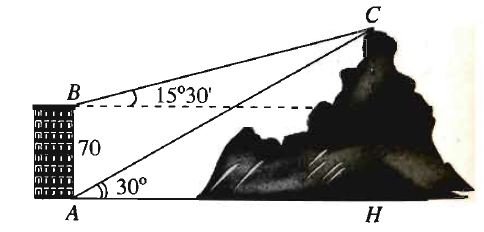
Câu 2: (1 điểm) Từ hai vị trí \(A\) và \(B\) của một tòa nhà, người ta quan sát đỉnh \(C\) của ngọn núi. Biết rằng độ cao \(AB = 70{\rm{m}}\), phương nhìn \(AC\) tạo với phương nằm ngang góc \({30^0}\), phương nhìn \(BC\) tạo với phương nằm ngang góc \({15^0}30’\). Tìm độ cao của ngọn núi đó có độ cao so với mặt đất.
Câu 3: (0,5 điểm) Tính giá trị các biểu thức sau:
\(P = 4\tan \left( {x + {4^0}} \right).\sin x\cot \left( {4x + {{26}^0}} \right)\) \( + \frac{{8{{\tan }^2}\left( {{3^0} – x} \right)}}{{1 + {{\tan }^2}\left( {5x + {3^0}} \right)}} + 8{\cos ^2}\left( {x – {3^0}} \right)\) khi \(x = {30^0}\)
—–HẾT—–
Giải đề 2
HƯỚNG DẪN GIẢI CHI TIẾT
I. Trắc nghiệm (7 điểm)
|
1. B
|
6. C
|
11. D
|
16. A
|
21. A
|
26. B
|
31. D
|
|
2.A
|
7. D
|
12. C
|
17. B
|
22. C
|
27. B
|
32. A
|
|
3. A
|
8. C
|
13. D
|
18. D
|
23. D
|
28. B
|
33. C
|
|
4. A
|
9. D
|
14. D
|
19. C
|
24. A
|
29. D
|
34. A
|
|
5. B
|
10. D
|
15. D
|
20. D
|
25. D
|
30. C
|
35. D
|
Câu 1 (NB):
Phương pháp:
Mệnh đề là câu khẳng định, có tính đúng hoặc sai.
Cách giải:
(1) và (4) là mệnh đề.
Chọn B.
Câu 2 (TH):
Phương pháp:
Phủ định của \(\forall \) là \(\exists \), phủ định của > là \( \le \).
Cách giải:
Mệnh đề phủ định của mệnh đề “\(\forall x \in \mathbb{R},{\kern 1pt} {\kern 1pt} x – 2 > 5\)” là “\(\exists x \in \mathbb{R},{\kern 1pt} {\kern 1pt} x – 2 \le 5\)”.
Chọn A.
Câu 3 (TH):
Phương pháp:
Viết tập hợp theo cách liệt kê các phần tử.
Cách giải:
Giải phương trình \(x\left( {x – 2} \right)\left( {x – 3} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 2}\\{x = 3}\end{array}} \right.\).
Mà \(x \in {\mathbb{N}^*} \Rightarrow x \in \left\{ {2;3} \right\}.\)
Vậy D = {2;3}.
Chọn A.
Câu 4 (TH):
Phương pháp:
Chỉ ra các tính chất đặc trưng cho các phần tử của tập hợp B và viết tập hợp B theo cách nêu tính chất đặc trưng cho các phần tử của tập hợp.
Cách giải:
B = {3;6;9;12;15}
\( \Rightarrow B = \left\{ {3n|n \in \mathbb{N},{\kern 1pt} {\kern 1pt} 1 \le n \le 5} \right\}\).
Chọn A.
Câu 5 (VD):
Phương pháp:
Thực hiện các phép toán trên tập hợp. Sử dụng trục số.
Cách giải:
+) \(A \cap B = \left( { – 3; – 2} \right]\)
=> A đúng.
+) \(A\backslash B = \left( { – \infty ; – 3} \right]\)

=> B sai.
+) \(A \cup B = \left( { – \infty ;5} \right]\)
=> C đúng.
+) \(B\backslash A = \left( { – 2;5} \right]\).
=> D đúng.
Chọn B.
Câu 6 (NB):
Phương pháp:
Tập hợp A được gọi là tập con của tập hợp B nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B.
Cách giải:
\({A_3} = \left\{ {4;5} \right\} \subset A = \left\{ {1;2;3;4;5} \right\}\).
Chọn C.
Câu 7 (NB):
Phương pháp:
Tìm khẳng định đúng.
Cách giải:
5 là số nguyên tố, 9, 12, 4 là hợp số nên mệnh đề D đúng.
Chọn D.
Câu 8 (TH):
Phương pháp:
Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là
\(ax + by \le c\) (\(ax + by \ge c\), \(ax + by < c\), \(ax + by > c\))
Trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.
Cách giải:
Ta có: \(2{x^2} + 1 \ge y + 2{x^2} \Leftrightarrow y – 1 \le 0\) nên đây là một bất phương trình bậc nhất hai ẩn.
Chọn C.
Câu 9 (NB):
Phương pháp:
Thay các tọa độ điểm vào bất phương trình, điểm nào thỏa mãn bất phương trình thì thuộc miền nghiệm của bất phương trình đó.
Cách giải:
+) Thay tọa độ điểm (5;1) vào bất phương trình ta có: 3.5 + 2.1 < 10 (Vô lí) => (5;1) không thuộc miền nghiệm của bất phương trình.
+) Thay tọa độ điểm (4;2) vào bất phương trình ta có: 3.4 + 2.2 < 10 (Vô lí) => (4;2) không thuộc miền nghiệm của bất phương trình.
+) Thay tọa độ điểm (1;5) vào bất phương trình ta có: 3.1 + 2.5 < 10 (Vô lí) => (1;5) không thuộc miền nghiệm của bất phương trình.
+) Thay tọa độ điểm (1;2) vào bất phương trình ta có: 3.1 + 2.2 < 10 (Đúng) => (1;2) không thuộc miền nghiệm của bất phương trình.
Chọn D.
Câu 10 (NB):
Phương pháp:
Sử dụng định lí cosin trong tam giác: \({a^2} = {b^2} + {c^2} – 2bc.\cos A.\)
Cách giải:
\(E{F^2} = E{G^2} + F{G^2} – 2EG.FG.\cos G\) là mệnh đề đúng.
Chọn D.
Câu 11 (TH):
Phương pháp:
Áp dụng định lí Sin trong tam giác ABC: \(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow \frac{{\sin B}}{{\sin C}} = \frac{{AC}}{{AB}}\).
Cách giải:
Áp dụng định lí Sin trong tam giác ABC ta có: \(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow \frac{{\sin B}}{{\sin C}} = \frac{{AC}}{{AB}}\).
Theo giả thiết \(\frac{{\sin B}}{{\sin C}} = \sqrt 3 \Rightarrow \frac{{AC}}{{AB}} = \sqrt 3 \Rightarrow AC = \sqrt 3 AB.\)
Vậy \(AC = \sqrt 3 .2\sqrt 2 = 2\sqrt 6 .\)
Chọn D.
Câu 12 (VD):
Phương pháp:
Tính sinA.
Tính diện tích tam giác ABC: \(S = \frac{1}{2}bc.\sin A.\)
Sử dụng định lí cosin trong tam giác tính a: \({a^2} = {b^2} + {c^2} – 2bc.\cos A.\)
Sử dụng công thức tính diện tích tam giác: \(S = \frac{1}{2}a{h_a}\), từ đó tính \({h_a}\).
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{{{\sin }^2}A + {{\cos }^2}A = 1}\\{ \Leftrightarrow {{\sin }^2}A + {{\left( {\frac{3}{5}} \right)}^2} = 1}\\{ \Leftrightarrow {{\sin }^2}A = \frac{{16}}{{25}}}\end{array}\)
Vì \({0^0} < A < {180^0}\) nên sinA > 0 \( \Rightarrow \sin A = \frac{4}{5}.\)
Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A. = \frac{1}{2}.7.5.\frac{4}{5} = 14.\)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{{a^2} = {b^2} + {c^2} – 2bc.\cos A.}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {7^2} + {5^2} – 2.7.5.\frac{3}{5}}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 32}\\{ \Rightarrow a = 4\sqrt 2 .}\end{array}\)
Lại có: \(S = \frac{1}{2}a{h_a} \Rightarrow {h_a} = \frac{{2S}}{a} = \frac{{2.14}}{{4\sqrt 2 }} = \frac{{7\sqrt 2 }}{2}.\)
Chọn C.
Câu 13 (TH):
Phương pháp:
Với x là nghiệm của phương trình đã cho thì mệnh đề P(x) là mệnh đề đúng.
Cách giải:
Ta có: \({x^2} – 5x + 4 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 4}\end{array}} \right.\).
Vậy với x = 1 thì P(x) là mệnh đề đúng.
Chọn D.
Câu 14 (NB):
Phương pháp:
Hệ bất phương trình bậc nhất hai ẩn là một hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn.
Cách giải:
\(\left\{ {\begin{array}{*{20}{l}}{x – 4 \ge y}\\{3x + 4y < 5}\end{array}} \right.\) là hệ bất phương trình bậc nhất hai ẩn.
Chọn D.
Câu 15 (NB):
Phương pháp:
Nhớ bảng giá trị lượng giác của các góc thường dùng hoặc sử dụng máy tính cầm tay.
Cách giải:
\(\begin{array}{*{20}{l}}{T = 2 + {{\sin }^2}{{90}^0} + 2{{\cos }^2}{{60}^0} – 3{{\tan }^2}{{45}^0}}\\{T = 2 + {1^2} + 2.{{\left( {\frac{1}{2}} \right)}^2} – {{3.1}^2}}\\{T = \frac{1}{2}.}\end{array}\)
Chọn D.
Câu 16 (NB):
Phương pháp:
Sử dụng các công thức tính diện tích tam giác: \({S_{ABC}} = \frac{1}{2}ab\sin C = pr = \frac{{abc}}{{4S}} = \frac{1}{2}c.{h_c}.\)
Cách giải:
\({S_{ABC}} = \frac{1}{2}ab\sin C\) nên đáp án A sai.
Chọn A.
Câu 17 (NB):
Phương pháp:
Áp dụng định lí Cosin trong tam giác: \(A{B^2} = B{C^2} + A{C^2} – 2BC.AC.\cos C\).
Cách giải:
Áp dụng định lí Cosin trong tam giác ABC:
\(\begin{array}{*{20}{l}}{A{B^2} = B{C^2} + A{C^2} – 2BC.AC.\cos C}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {1^2} + {3^2} – 2.1.3.\cos {{60}^0} = 7}\\{ \Rightarrow AB = \sqrt 7 .}\end{array}\)
Chọn B.
Câu 18 (NB):
Phương pháp:
Mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) là \(Q \Rightarrow P\).
Cách giải:
Mệnh đề đảo của mệnh đề “Nếu tứ giác là một hình thoi thì tứ giác đó nội tiếp được một đường tròn” là
Chọn D.
Câu 19 (NB):
Phương pháp:
Biểu diễn tập hợp trên trục số.
Cách giải:
Hình vẽ đã cho là minh họa cho tập hợp \(\left[ {1; + \infty } \right).\)
Chọn C.
Câu 20 (NB):
Phương pháp:
Sử dụng mối liên hệ giá trị lượng giác của hai góc bù nhau: Cho \(\alpha \) và \(\beta \) là hai góc khác nhau và bù nhau ta có: \(\sin \alpha = \sin \beta ,\) \(\cos \alpha = – \cos \beta \), \(\tan \alpha = – \tan \beta \), \(\cot \alpha = – \cot \beta .\)
Cách giải:
\(\alpha \) và \(\beta \) là hai góc khác nhau và bù nhau nên \(\sin \alpha = \sin \beta ,\) \(\cos \alpha = – \cos \beta \), \(\tan \alpha = – \tan \beta \), \(\cot \alpha = – \cot \beta .\)
Vậy đẳng thức ở đáp án D sai.
Chọn D.
Câu 21 (TH):
Phương pháp:
\({C_B}A = B\backslash A = \{ x|x \in B\) và \(x \notin A\)}.
Cách giải:
Ta có: \({C_B}A = B\backslash A = \{ x|x \in B\) và \(x \notin A\)}.
\( \Rightarrow {C_B}A = \left\{ {3;5;7;8} \right\}.\)
Chọn A.
Câu 21 (VD):
Phương pháp:
Sử dụng hệ quả định lí cosin trong tam giác ABC tính cosB: \(\cos B = \frac{{A{B^2} + B{C^2} – A{C^2}}}{{2AB.BC}}\).
Tính BM, CM.
Sử dụng định lí cosin trong tam giác ABM tính AM: \(A{M^2} = A{B^2} + B{M^2} – 2AB.BM.\cos B\).
Cách giải:
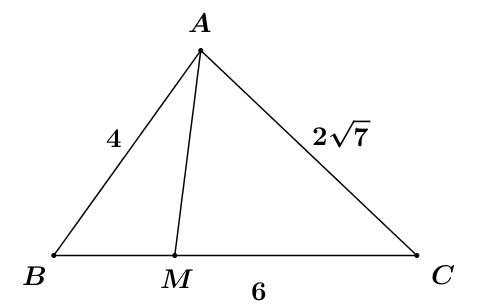
Ta có:
\(\begin{array}{*{20}{l}}{\cos B = \frac{{A{B^2} + B{C^2} – A{C^2}}}{{2AB.BC}}}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{{4^2} + {6^2} – {{\left( {2\sqrt 7 } \right)}^2}}}{{2.4.6}} = \frac{1}{2}}\end{array}\)
Vì MC = 2MB, BC = 6 nên \(BM = \frac{1}{3}BC = \frac{1}{3}.6 = 2.\)
Áp dụng định lí cosin trong tam giác ABM ta có:
\(\begin{array}{*{20}{l}}{A{M^2} = A{B^2} + B{M^2} – 2AB.BM.\cos B}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {4^2} + {2^2} – 2.4.2.\frac{1}{2} = 12}\\{ \Rightarrow AM = 2\sqrt 3 .}\end{array}\)
Chọn C.
Câu 23 (TH):
Phương pháp:
Tìm phương trình đường thẳng d. Loại đáp án.
Thay tọa độ điểm O(0;0) vào các bất phương trình chưa bị loại ở các đáp án, tiếp tục loại đáp án.
Cách giải:
Đường thẳng d đi qua điểm (0;1) nên loại đáp án B, C.
Ta thấy điểm O(0;0) không thuộc miền nghiệm của bất phương trình.
+ Thay tọa độ điểm O(0;0) vào bất phương trình \(2x + y < 1\) ta có: 2.0 + 0 < 1 (Đúng) => Loại.
+ Thay tọa độ điểm O(0;0) vào bất phương trình \(2x + y > 1\) ta có: 2.0 + 0 > 1 (Vô lí) => Thỏa mãn.
Chọn D.
Câu 24 (TH):
Phương pháp:
Sử dụng công thức: \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}.\)
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1 + {{\tan }^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}}\\{ \Leftrightarrow 1 + {{\left( { – 2\sqrt 2 } \right)}^2} = \frac{1}{{{{\cos }^2}\alpha }}}\\{ \Leftrightarrow {{\cos }^2}\alpha = \frac{1}{9}}\\{ \Leftrightarrow \cos \alpha = \pm \frac{1}{3}}\end{array}\)
Vì \({0^0} < \alpha < {180^0}\) \( \Rightarrow \sin \alpha > 0\). Mà \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} < 0\) nên \(\cos \alpha < 0\).
Vậy \(\cos \alpha = – \frac{1}{3}.\)
Chọn A.
Câu 25 (VD):
Phương pháp:
Hướng N300E là hướng tạo với hướng bắc một góc 300 và tạo với hướng đông một góc \({90^0} – {30^0} = {60^0}\).
Áp dụng định lí cosin trong tam giác.
Cách giải:
Hướng N300E là hướng tạo với hướng bắc một góc 300 và tạo với hướng đông một góc \({90^0} – {30^0} = {60^0}\).
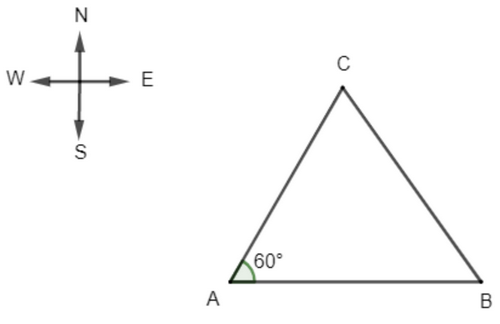
A là vị trí cảng.
Ca nô đi theo hướng đông từ A đến B, sau 3 giờ đi được quãng đường AB = 50.3 = 150 (km).
Tàu cá đi theo hướng N300E từ A đến C, sau 3 giờ đi được quãng đường AC = 40.3 = 120 (km).
Áp dụng định lí Cosin trong tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{B{C^2} = A{B^2} + A{C^2} – 2AB.AC.\cos {{60}^{}}}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {{150}^2} + {{120}^2} – 2.150.120.\frac{1}{2}}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 18{\kern 1pt} 900}\\{ \Rightarrow BC = 30\sqrt {21} \approx 137,5.}\end{array}\)
Vậy sau 3 giờ hai tàu cách nhau khoảng 137,5km.
Chọn D.
Câu 26.
Cách giải
Sử dụng máy tính cầm tay, ta được \(\sqrt 3 = 1,7320508076…\)
Làm tròn đến hàng phần nghìn ta được kết quả: $1,732$.
Chọn B.
Câu 27.
Cách giải
Ta có: \(h = 347,13{\rm{m}} \pm 0,2{\rm{m}} \Rightarrow d = 0,2\)
Độ chính xác d có chữ số (khác 0) ở hàng lớn nhất là hàng phần mười, do đó ta làm tròn số gần đúng \(h = 347,13\) đến hàng đơn vị, kết quả là $347$.
Chọn B
Câu 28 (TH)
Phương pháp:
Trung bình
\(\bar x = \frac{{{m_1}{x_1} + {m_2}{x_2} + … + {m_k}{x_k}}}{n}\) trong đó mk là tần số của giá trị xk và \(n = {m_1} + {m_2} + … + {m_k}\)
Cách giải:
Khối lượng trung bình của cả ba nhóm học sinh là: \(\bar x = \frac{{20.50 + 15.38 + 25.40}}{{20 + 15 + 25}} = 42,8.\)
Chọn B.
Câu 29 (VD):
Phương pháp:
Áp dụng công thức tìm phương sai và độ lệch chuẩn.
Cách giải:
Số trung bình cộng:
\(\bar x = \frac{{9.1 + 10.1 + 11.3 + 12.5 + 13.8 + 14.13 + 15.19 + 16.24 + 17.14 + 18.10 + 19.2}}{{100}}\)\( = \frac{{1523}}{{100}} = 15,23\) (điểm)
Phương sai:
\({s^2} = \frac{1}{{100}}\left[ {1.{{\left( {9 – 15,23} \right)}^2} + 1.{{\left( {10 – 15,23} \right)}^2} + \; \ldots \; + 10.{{\left( {18 – 15,23} \right)}^2} + 2.{{\left( {19 – 15,23} \right)}^2}} \right]\) \( = 3,9571\)(điểm)
Độ lệch chuẩn:
\(s = \sqrt {{s^2}} \)\( = \sqrt {3,9571} \; \approx 1,989{\rm{2}}\) (điểm)
Vậy phương sai nhỏ hơn \(4\), độ lệch chuẩn nhỏ hơn \(2\).
Chọn D.
Câu 30.
Cách giải:
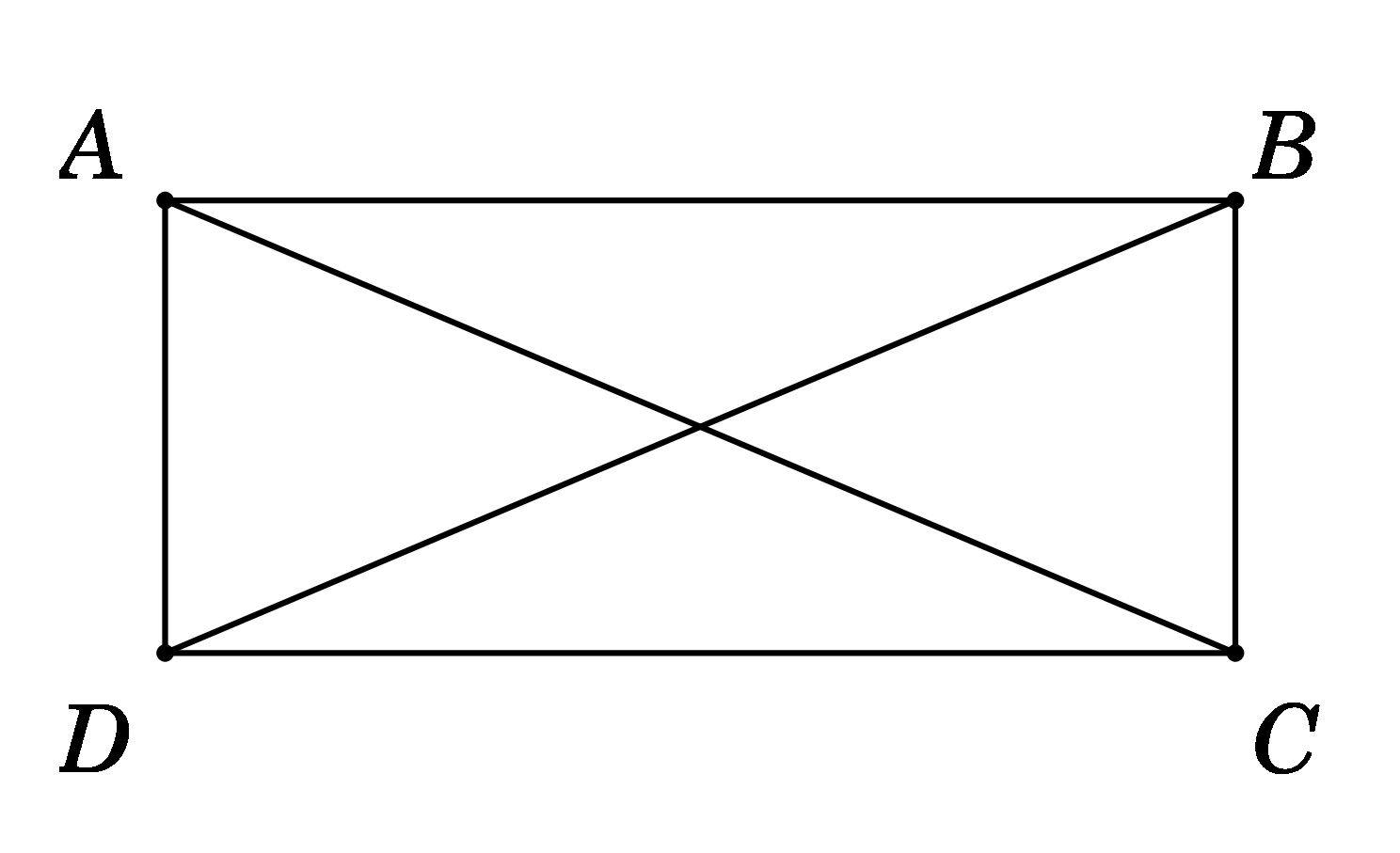
Ta có \(\left\{ {\begin{array}{*{20}{l}}{\left| {\overrightarrow {AB} – \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = BD}\\{\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = AC}\end{array}} \right..\)
Mà \(BD = AC \Rightarrow \left| {\overrightarrow {AB} – \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} + \overrightarrow {AD} } \right|.\)
Chọn C.
Câu 31.
Cách giải:
Ta có \(\overrightarrow {MA} – \overrightarrow {MB} + \overrightarrow {MC} = \vec 0 \Leftrightarrow \overrightarrow {BA} + \overrightarrow {MC} = \vec 0 \Leftrightarrow \overrightarrow {MC} = \overrightarrow {AB} \)
\( \Rightarrow MABC\) là hình bình hành
\( \Rightarrow \overrightarrow {MA} = \overrightarrow {CB} .\)
Do đó D sai.
Chọn D.
Câu 32.
Cách giải:
Vì ABCD là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \) hay \(\overrightarrow {AB} + \overrightarrow {CD} = \vec 0\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} }\\{\overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {CD} }\end{array}} \right.\)\( \Rightarrow \overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {BC} + \overrightarrow {AB} + \overrightarrow {CD} = 2\overrightarrow {BC} \)
Vậy A đúng.
\(\overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \) => B sai.
\(\overrightarrow {AC} – \overrightarrow {BD} = \overrightarrow {AB} – \overrightarrow {CD} = \overrightarrow {DC} + \overrightarrow {DC} = 2\overrightarrow {DC} = – 2\overrightarrow {CD} \) => C sai
\(\overrightarrow {AC} – \overrightarrow {AD} = \overrightarrow {DC} \) => D sai.
Chọn A.
Câu 33.
Cách giải:
Ta có: \(OA = OB = a\)
\( \Rightarrow \left| {2\overrightarrow {OA} } \right| + \left| {3\overrightarrow {OB} } \right| = 2a + 3a = 5a\). Vậy B đúng.
Tương tự, ta có \(\left| {11\overrightarrow {OA} } \right| – \left| {6\overrightarrow {OB} } \right| = 11a – 6a = 5a\). Do đó D đúng.
Lấy C, D sao cho \(\overrightarrow {OC} = 3\overrightarrow {OA} ;\overrightarrow {OD} = 4\overrightarrow {OB} ;\)
Dựng hình bình hành OCED. Do \(\widehat {AOB} = {90^^\circ }\) nên OCED là hình chữ nhật.
Ta có: \(3\overrightarrow {OA} + 4\overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {OE} \)
\( \Rightarrow \left| {3\overrightarrow {OA} + 4\overrightarrow {OB} } \right| = \left| {\overrightarrow {OE} } \right| = OE\)
Lại có: \(OC = 3OA = 3a,OD = 4OB = 4a.\)
\( \Rightarrow OE = \sqrt {O{C^2} + C{E^2}} = \sqrt {O{C^2} + O{D^2}} = \sqrt {{{(3a)}^2} + {{(4a)}^2}} = 5a\)
Do đó A đúng.
Chọn C
Câu 34.
Cách giải:
Vì M là trung điểm của BC suy ra \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \)
Khi đó \(\overrightarrow {AM} .\overrightarrow {BC} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\overrightarrow {BC} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {BA} + \overrightarrow {AC} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {AC} – \overrightarrow {AB} } \right) = \frac{1}{2}\left( {{{\overrightarrow {AC} }^2} – {{\overrightarrow {AB} }^2}} \right) = \frac{1}{2}\left( {A{C^2} – A{B^2}} \right) = \frac{{{b^2} – {c^2}}}{2}\)
Chọn A.
Câu 35.
Cách giải:
Ta có \(\left\{ \begin{array}{l}BD = a\sqrt 2 \\\overrightarrow {BC} + \overrightarrow {BD} + \overrightarrow {BA} = \left( {\overrightarrow {BC} + \overrightarrow {BA} } \right) + \overrightarrow {BD} = \overrightarrow {BD} + \overrightarrow {BD} = 2\overrightarrow {BD} \end{array} \right.\)
Khi đó \(P = \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).2\overrightarrow {BD} = 2\overrightarrow {AB} .\overrightarrow {BD} + 2\overrightarrow {AC} .\overrightarrow {BD} = – 2\overrightarrow {BA} .\overrightarrow {BD} + \vec 0\)
\( = – 2BA.BD\cos \left( {\overrightarrow {BA} ,\overrightarrow {BD} } \right) = – 2.a.a\sqrt 2 .\frac{{\sqrt 2 }}{2} = – 2{a^2}\)
Chọn D.
II. Tự luận (3 điểm)
Câu 1 (TH):
Cách giải:
a) Ta có:
\( = \overrightarrow {{\rm{MA}}} \cdot (\overrightarrow {{\rm{MC}}} – \overrightarrow {{\rm{MB}}} ) + \overrightarrow {{\rm{MB}}} (\overrightarrow {{\rm{MA}}} – \overrightarrow {{\rm{MC}}} ) + \overrightarrow {{\rm{MC}}} (\overrightarrow {{\rm{MB}}} – \overrightarrow {{\rm{MA}}} ) = \)
\( = \overrightarrow {{\rm{MA}}} \cdot \overrightarrow {{\rm{MC}}} – \overrightarrow {{\rm{MA}}} \cdot \overrightarrow {{\rm{MB}}} + \overrightarrow {{\rm{MB}}} \cdot \overrightarrow {{\rm{MA}}} – \overrightarrow {{\rm{MB}}} \cdot \overrightarrow {{\rm{MC}}} + \overrightarrow {{\rm{MC}}} \cdot \overrightarrow {{\rm{MB}}} – \overrightarrow {{\rm{MC}}} \cdot \overrightarrow {{\rm{MA}}} \)
\( = \overrightarrow {{\rm{MA}}} \cdot \overrightarrow {{\rm{MC}}} – \overrightarrow {{\rm{MC}}} \cdot \overrightarrow {{\rm{MA}}} – \overrightarrow {{\rm{MA}}} \cdot \overrightarrow {{\rm{MB}}} + \overrightarrow {{\rm{MB}}} \cdot \overrightarrow {{\rm{MA}}} – \overrightarrow {{\rm{MB}}} \cdot \overrightarrow {{\rm{MC}}} + \overrightarrow {{\rm{MC}}} \cdot \overrightarrow {{\rm{MB}}} = 0\)
b)
\({\rm{M}}{{\rm{A}}^2} = {\overrightarrow {{\rm{MA}}} ^2} = {(\overrightarrow {{\rm{MG}}} + \overrightarrow {{\rm{GA}}} )^2} = {\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + 2\overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GA}}} \)
\({\rm{M}}{{\rm{B}}^2} = {\overrightarrow {{\rm{MB}}} ^2} = {(\overrightarrow {{\rm{MG}}} + \overrightarrow {{\rm{GB}}} )^2} = {\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{B}}^2} + 2\overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GB}}} \)
\({\rm{M}}{{\rm{C}}^2} = {\overrightarrow {{\rm{MC}}} ^2} = {(\overrightarrow {{\rm{MG}}} + \overrightarrow {{\rm{GC}}} )^2} = {\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{C}}^2} + 2\overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GC}}} \)
\( \Rightarrow {\rm{M}}{{\rm{A}}^2} + {\rm{M}}{{\rm{B}}^2} + {\rm{M}}{{\rm{C}}^2} = 3{\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2} + 2(\overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GA}}} + \overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GB}}} + \overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GC}}} )\)
\( = 3{\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2} + 2\overrightarrow {{\rm{MG}}} (\overrightarrow {{\rm{GA}}} + \overrightarrow {{\rm{GB}}} + \overrightarrow {{\rm{GC}}} ) = 3{\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2}\)
c) Vì \({\rm{M}}{{\rm{A}}^2} + {\rm{M}}{{\rm{B}}^2} + {\rm{M}}{{\rm{C}}^2} = 3{\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2}\) đúng với M bất kì.
Chọn \({\rm{M}} \equiv {\rm{A}}\) ta được:
\({\rm{A}}{{\rm{A}}^2} + {\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} = 3{\rm{A}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2}\)
\( \Leftrightarrow {\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} = 4{\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2}\)
Tương tự,
\({\rm{M}} \equiv {\rm{B}} \Rightarrow {\rm{B}}{{\rm{A}}^2} + {\rm{B}}{{\rm{C}}^2} = 4\;{\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{C}}^2}\)
\({\rm{M}} \equiv {\rm{C}} \Rightarrow {\rm{C}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} = 4{\rm{G}}{{\rm{C}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{A}}^2}\)
Thay \(AB = c,AC = b,BC = a\)
\(\begin{array}{*{20}{l}}{ \Rightarrow 6\left( {{\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2}} \right) = 2\left( {{{\rm{a}}^2} + {{\rm{b}}^2} + {{\rm{c}}^2}} \right)}\\{ \Leftrightarrow {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2} = \frac{1}{3}\left( {{{\rm{a}}^2} + {{\rm{b}}^2} + {{\rm{c}}^2}} \right)}\end{array}\)
Câu 2 (VD):
Cách giải:
Từ giả thiết, ta suy ra tam giác ABC có
\(\widehat {CAB} = {60^^\circ },\widehat {ABC} = {105^^\circ }30’\)và \(c = 70\)
Khi đó \(\hat A + \hat B + \hat C = {180^^\circ } \Leftrightarrow \hat C = {180^^\circ } – \left( {\hat A + \hat B} \right) = {180^^\circ } – {165^^\circ }30′ = {14^^\circ }30’\)
Theo định lí sin, ta có \(\frac{b}{{\sin B}} = \frac{c}{{\sin C}}\) hay \(\frac{b}{{\sin {{105}^^\circ }30′}} = \frac{{70}}{{\sin {{14}^^\circ }30′}}\)
Do đó \(AC = b = \sin {105^^\circ }30’\frac{{70}}{{\sin {{14}^^\circ }30′}} \approx 269,4m\)
Gọi CH là khoảng cách từ C đến mặt đất. Tam giác vuông ACH có cạnh CH đối diện với góc \({30^^\circ }\) nên \(CH = \frac{{AC}}{2} = \frac{{269,4}}{2} = 134,7m\)
Vậy ngọn núi cao khoảng 135m.
Câu 3 (VDC):
Phương pháp:
Thay \(x = {30^0}\), sử dụng mối quan hệ giá trị lượng giác của hai góc bù nhau.
Cách giải:
Thay \(x = {30^0}\) ta có:
\(\begin{array}{*{20}{l}}{P = 4\tan \left( {{{30}^0} + {4^0}} \right).\sin {{30}^0}\cot \left( {{{4.30}^0} + {{26}^0}} \right) + \frac{{8{{\tan }^2}\left( {{3^0} – {{30}^0}} \right)}}{{1 + {{\tan }^2}\left( {{{5.30}^0} + {3^0}} \right)}} + 8{{\cos }^2}\left( {{{30}^0} – {3^0}} \right)}\\{P = 4\tan {{34}^0}.\sin {{30}^0}\cot {{146}^0} + \frac{{8{{\tan }^2}\left( { – {{27}^0}} \right)}}{{1 + {{\tan }^2}{{153}^0}}} + 8{{\cos }^2}{{27}^0}}\\{P = 4\tan {{34}^0}.\sin {{30}^0}\cot \left( {{{180}^0} – {{34}^0}} \right) + 8{{\tan }^2}{{27}^0}{{\cos }^2}{{153}^0} + 8{{\cos }^2}{{27}^0}}\\{P = – 4\tan {{34}^0}.\sin {{30}^0}\cot {{34}^0} + 8{{\tan }^2}{{27}^0}{{\cos }^2}\left( {{{180}^0} – {{27}^0}} \right) + 8{{\cos }^2}{{27}^0}}\\{P = – 4.\sin {{30}^0} + 8{{\tan }^2}{{27}^0}{{\cos }^2}{{27}^0} + 8{{\cos }^2}{{27}^0}}\\{P = – 4.\sin {{30}^0} + 8{{\cos }^2}{{27}^0}\left( {{{\tan }^2}{{27}^0} + 1} \right)}\\{P = – 4.\sin {{30}^0} + 8{{\cos }^2}{{27}^0}\frac{1}{{{{\cos }^2}{{27}^0}}}}\\{P = – 4.\frac{1}{2} + 8}\\{P = 6}\end{array}\)
Đề 3
Phần 1: Trắc nghiệm (30 câu – 6 điểm)
Câu 1: Cho các phát biểu sau đây:
(1) “17 là số nguyên tố”.
(2) “Tam giác vuông có một đường trung tuyến bằng nửa cạnh huyền”.
(3) “Các em C14 hãy cố gắng học tập thật tốt nhé!”
(4) “Mọi hình chữ nhật đều nội tiếp được đường tròn”.
Hỏi có bao nhiêu phát biểu là mệnh đề?
A. 4. B. 3. C. 2. D. 1.
Câu 2: Giả sử biết số đúng là 8217,3. Sai số tuyệt đối khi quy tròn số này đến hàng chục là:
A. 7,3. B. 2,3. C. 0,3. D. 2,7.
Câu 3: Cho tam giác ABC có trung tuyến AM. Đặt \(\vec a{\rm{ \;}} = \overrightarrow {AB} ,{\mkern 1mu} {\mkern 1mu} \vec b{\rm{ \;}} = \overrightarrow {AM} \). Giả sử \(\overrightarrow {AC} {\rm{ \;}} = x\vec a{\rm{ \;}} + y\vec b,{\mkern 1mu} {\mkern 1mu} ,x,{\mkern 1mu} {\mkern 1mu} y \in \mathbb{R}\). Tìm cặp số (x;y) tương ứng.
A. (-1;-2). B. (1;2). C. (-1;2). D. (1;-2).
Câu 4: Lớp 10A có 37 học sinh, trong đó có 17 học sinh thích môn Văn, 19 học sinh thích môn Toán, 9 em không thích môn Văn và Toán. Số học sinh tích cả hai môn Văn và Toán là:
A. 13. B. 8. C. 6. D. 2.
Câu 5: Tìm tập nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x – 4 \ge 0}\\{\frac{{x – 1}}{2} – x \ge {\rm{ \;}} – 2}\end{array}} \right.\).
A. \(S = \left[ {3; + \infty } \right).\) B. \(S = \left[ {\frac{4}{3};3} \right].\) C. \(S = \left[ {\frac{4}{3}; + \infty } \right).\) D. \(S = \emptyset .\)
Câu 6: Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y – 1 > 0}\\{y \ge 2}\\{ – x + 2y > 3}\end{array}} \right.\) là phần không tô đậm của hình vẽ nào trong các hình vẽ sau:
A. 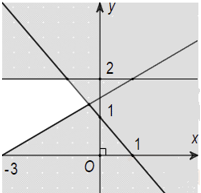 B.
B. 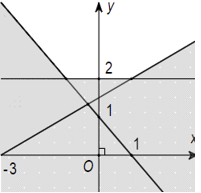 C.
C.  D.
D. 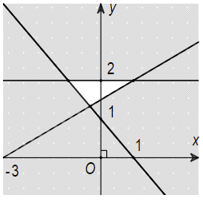
Câu 7: Cho tam giác ABC có AB = 9, AC = 18 và A = 600. Bán kính R của đường tròn ngoại tiếp tam giác ABC là:
A. 3. B. \(9\sqrt 3 .\) C. 9. D. 6.
Câu 8: Một người ngồi trên tàu hỏa đi từ ga A đến ga B. Khi đỗ tàu ở ga A, qua ống nhòm người đó nhìn thấy một tháp C. Hướng nhìn từ người đó đến tháp tạo với hướng đi của tàu một góc 600. Khi tàu đỗ ở ga B, người đó nhìn lại vẫn thấy tháp C, hướng nhìn từ người đó đến tháp tạo với hướng ngược với hướng đi của tàu một góc 450. Biết rằng đoạn đường tàu nối thẳng ga A với ga B dài 8km. Hỏi khoảng cách từ ga A đến tháp C gần nhất với số nào sau đây?

A. 5,9. B. 5,86. C. 5,78. D. 5,8.
Câu 9: Biểu thức \({\tan ^2}x{\sin ^2}x – {\tan ^2}x + {\sin ^2}x\) có giá trị bằng
A. -1. B. 0. C. 2. D. 1.
Câu 10: Gọi AN, CM là các đường trung tuyến của tam giác ABC. Đẳng thức nào sau đây đúng?
A. \(\overrightarrow {AB} {\rm{ \;}} = \frac{2}{3}\overrightarrow {AN} {\rm{ \;}} + \frac{2}{3}\overrightarrow {CM} \). B. \(\overrightarrow {AB} {\rm{ \;}} = \frac{4}{3}\overrightarrow {AN} {\rm{ \;}} – \frac{2}{3}\overrightarrow {CM} \). C. \(\overrightarrow {AB} {\rm{ \;}} = \frac{4}{3}\overrightarrow {AN} {\rm{ \;}} + \frac{4}{3}\overrightarrow {CM} \). D. \(\overrightarrow {AB} {\rm{ \;}} = \frac{4}{3}\overrightarrow {AN} {\rm{ \;}} + \frac{2}{3}\overrightarrow {CM} \).
Câu 11: Điểm thi của 32 học sinh trong kì thi Tiếng Anh (thang điểm 100) như .sau:

Độ lệch chuẩn là:
A. \(s \approx 13,793\) B. \(s \approx 19,973\) C. \(s \approx 17,393\) D. \(s \approx 13,933\)
Câu 12: Gọi G là trọng tâm của tam giác ABC, nếu điểm M thỏa mãn hệ thức \(\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} + 4\overrightarrow {MC} {\rm{ \;}} = \vec 0\) thì vị trí của điểm M thuộc miền nào trong hình vẽ?
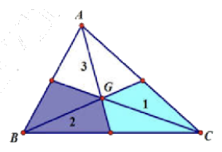
A. Miền 1. B. Miền 2. C. Miền 3. D. ở ngoài tam giác ABC.
Câu 13: Tứ giác ABCD thỏa mãn điều kiện: \(\overrightarrow {DB} {\rm{ \;}} = m\overrightarrow {DC} {\rm{ \;}} + \overrightarrow {DA} {\mkern 1mu} {\mkern 1mu} \left( {m > 0} \right)\) là:
A. Hình thang. B. Hình bình hành. C. Hình chữ nhật. D. Hình thoi.
Câu 14: Trong tam giác ABC, hệ thức nào sau đây sai?
A. \(a = \frac{{b\sin A}}{{\sin B}}.\) B. \(b = R.\tan B.\) C. \(\sin C = \frac{{c\sin A}}{a}.\) D. \(a = 2R\sin A.\)
Câu 15: Để đo độ phân tán (độ chênh lệch) giữa các giá trị của mẫu số liệu so với số trung bình, người ta sử dụng số đặc trưng nào sau đây?
A. Phương sai B. Độ lệch chuẩn C. Cả A và B đúng D. Cả A và B sai
Câu 16: Sản lượng lúa của 40 thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng tần số sau đây: (đơn vị: tạ)

Phương sai là
A. 1,24 B. 1,54 C. 22,1 D. 4,70
Câu 17: Cho tập hợp \(A = \left\{ {x \in \mathbb{N}|x < 5} \right\}\). Tập hợp A viết lại bằng cách liệt kê các phần tử là
A. \(A = \left\{ {1,2,3,4,5} \right\}\) B. \(A = \left\{ {1,2,3,4} \right\}\) C. \(A = \left\{ {0,1,2,3,4,5} \right\}\) D. \(A = \left( {0,5} \right)\)
Câu 18: Cho hai tập hợp \(X = \left\{ {1;2;3;4} \right\}\), \(Y = \left\{ {1;2} \right\}\). Tập hợp \({C_X}Y\) là tập hợp nào sau đây?
A. \(\left\{ {3;4} \right\}.\) B. \(\left\{ {1;2;3;4} \right\}.\) C. \(\left\{ {1;2} \right\}.\) D. \(\emptyset .\)
Câu 19: Phần không tô đậm trong hình vẽ dưới đây (không chứa biên), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
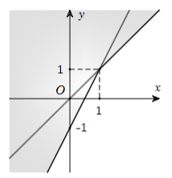
A. \(\left\{ {\begin{array}{*{20}{l}}{x – y < 0}\\{2x – y < 1}\end{array}} \right..\) B. \(\left\{ {\begin{array}{*{20}{l}}{x – y > 0}\\{2x – y < 1}\end{array}} \right..\) C. \(\left\{ {\begin{array}{*{20}{l}}{x – y > 0}\\{2x – y > 1}\end{array}} \right..\) D. \(\left\{ {\begin{array}{*{20}{l}}{x – y < 0}\\{2x – y > 1}\end{array}} \right..\)
Câu 20: Trong hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 3y – 2 \ge 0}\\{2x + y + 1 \le 0}\end{array}} \right.\). Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
A. A(0;1). B. C(1;3). C. B(-1;1). D. D(-1;0).
Câu 21: Cho \(\sin x = \frac{3}{5},{\mkern 1mu} {\mkern 1mu} {90^0} < x < {180^0}\). Giá trị biểu thức \(P = \tan x.{\cos ^2}x\) bằng:
A. \(\frac{{12}}{{25}}.\) B. \(\frac{{25}}{{12}}.\) C. \( – \frac{{25}}{{12}}.\) D. \( – \frac{{12}}{{25}}.\)
Câu 22: Cho \(\tan \alpha {\rm{ \;}} = {\rm{ \;}} – 2\). Tính giá trị của biểu thức \(P = \frac{{2\sin \alpha {\rm{ \;}} + 3\cos \alpha }}{{3\sin \alpha {\rm{ \;}} – 2\cos \alpha }}\).
A. \(P = \frac{7}{4}.\) B. \(P = {\rm{ \;}} – \frac{1}{8}.\) C. \(P = {\rm{ \;}} – \frac{7}{4}.\) D. \(P = \frac{1}{8}.\)
Câu 23: Cho tam giác ABC có trung tuyến BM và trọng tâm \(G\). Đặt \(\overrightarrow {BC} {\rm{\;}} = \vec a,{\mkern 1mu} {\mkern 1mu} \overrightarrow {BA} {\rm{\;}} = b\). Hãy phân tích vectơ \(\overrightarrow {BG} \) theo \(\vec a\) và \(\vec b\).
A. \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\) B. \(\overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\vec a + \frac{2}{3}\vec b\) C. \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{2}{3}\vec b\) D. \(\overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\vec a + \frac{1}{3}\vec b\)
Câu 24: Khẳng định nào sau đây là sai?
A. Ba điểm phân biệt \(A,{\mkern 1mu} {\mkern 1mu} B,{\mkern 1mu} {\mkern 1mu} C\) thẳng hàng khi và chỉ khi \(\overrightarrow {AB} {\rm{\;}} = k\overrightarrow {BC} ,k \ne 0\).
B. Ba điểm phân biệt \(A,{\mkern 1mu} {\mkern 1mu} B,{\mkern 1mu} {\mkern 1mu} C\) thẳng hàng khi và chỉ khi \(\overrightarrow {AC} = k\overrightarrow {BC} ,k \ne 0\).
C. Ba điểm phân biệt \(A,{\mkern 1mu} {\mkern 1mu} B,{\mkern 1mu} {\mkern 1mu} C\) thẳng hàng khi và chỉ khi \(\overrightarrow {AB} {\rm{\;}} = k\overrightarrow {AC} ,k \ne 0\).
D. Ba điểm phân biệt \(A,B,C\) thẳng hàng khi và chỉ khi \(\overrightarrow {AB} {\rm{\; = \;}}k\overrightarrow {AC} \).
Câu 25: Cho tam giác ABC biết AB = 5, AC = 7, BC = 6. Bán kính đường tròn nội tiếp tam giác xấp xỉ là:
A. 1,63 B. 1,71 C. 1,36 D. 1,06
Câu 26: Thực hiện đo chiều dài của bốn cây cầu, kết quả đo đạc nào trong các kết quả sau đây là chính xác nhất?
A. \(15,34m \pm 0,01m.\) B. \(1527,4m \pm 0,2m.\) C. \(2135,8m \pm 0,5m.\) D. \(63,47m \pm 0,15m.\)
Câu 27: Khoảng tứ phân vị của mẫu số liệu 1 1 1 2 2 2 3 3 4 20 là:
A. 2. B. 1. C. 3. D. 4.
Câu 28: Cho số \(x = \frac{2}{7}\). Cho các giá trị gần đúng của x là 0,28; 0,29; 0,286; 0,287. Giá trị gần đúng nào là tốt nhất
A. 0,28. B. 0,29. C. 0,286. D. 0,287.
Câu 29: Cho ba điểm không thẳng hàng A, B, C. Điều kiện cần và đủ để ba điểm A, B, C thỏa mãn điều kiện \(\left( {\overrightarrow {CA} {\rm{ \;}} + \overrightarrow {CB} } \right).\overrightarrow {AB} {\rm{ \;}} = 0\) là:
A. \(\Delta ABC\) đều. B. \(\Delta ABC\) cân tại C.
C. \(\Delta ABC\) vuông tại C. D. \(\Delta ABC\) vuông cân tại C.
Câu 30: Cho tam giác ABC vuông cân tại A, cạnh AC = a. Tính \(\overrightarrow {AB} .\overrightarrow {AC} \).
A. \(\overrightarrow {AB} .\overrightarrow {AC} {\rm{ \;}} = \vec 0.\) B. \(\overrightarrow {AB} .\overrightarrow {AC} {\rm{ \;}} = {a^2}.\) C. \(\overrightarrow {AB} .\overrightarrow {AC} {\rm{ \;}} = 0.\) D. \(\overrightarrow {AB} .\overrightarrow {AC} {\rm{ \;}} = \sqrt 2 {a^2}.\)
Phần 2: Tự luận (4 điểm)
Câu 1: Trong một cuộc thi nghề, người ta ghi lại thời gian hoàn thành một sản phẩm của một số thí sinh ở bảng sau:

a) Hãy tìm số trung bình, tứ phân vị và mốt của thời gian thi nghề của các thí sinh trên.
b) Năm ngoái, thời gian thi của các thí sinh có số trung bình và trung vị đều bằng nhau 7. Bạn hãy so sánh thời gian thi nói chung của các thí sinh trong hai năm.
Câu 2: Cho tam giác ABC.
Tìm tập hợp các điểm M thỏa mãn điều kiện \(\left| {\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA} {\rm{ \;}} – 3\overrightarrow {MC} } \right|\).
Câu 3: Cho tam giác ABC có ba cạnh là a, b, c. Chứng minh rằng
\(\frac{{{a^2} + {b^2} + {c^2}}}{{2abc}} = \frac{{\cos A}}{a} + \frac{{\cos B}}{b} + \frac{{\cos C}}{c}\).
—– HẾT —–
Giải đề 3
HƯỚNG DẪN GIẢI CHI TIẾT
Phần 1: Trắc nghiệm (30 câu – 6 điểm)
|
1.B
|
2.D
|
3.C
|
4.B
|
5.C
|
6.C
|
7.C
|
8.B
|
9.B
|
10.D
|
|
11.A
|
12.A
|
13.A
|
14.B
|
15.C
|
16.B
|
17.C
|
18.A
|
19.C
|
20.C
|
|
21.D
|
22.D
|
23.A
|
24.D
|
25.A
|
26.C
|
27.A
|
28.C
|
29.B
|
30.C
|
Câu 1 (NB):
Phương pháp:
Mệnh đề là câu khẳng định có tính đúng hoặc sai.
Cách giải:
Câu (3) không phải là mệnh đề.
Chọn B.
Câu 2 (TH):
Phương pháp:
Tìm số quy tròn a của \(\bar a = 8217,3\) đến hàng chục.
Tính sai số tuyệt đối \(\Delta {\rm{ \;}} = \left| {\bar a – a} \right|\).
Cách giải:
Quy tròn \(\bar a = 8217,3\) đến hàng chục ta được số gần đúng \(a = 8220\).
Vậy sai số tuyệt đối là: \(\Delta {\rm{ \;}} = \left| {\bar a – a} \right| = 2,7.\)
Chọn D.
Câu 3 (TH):
Phương pháp:
Sử dụng công thức trung điểm: \(\overrightarrow {AM} {\rm{ \;}} = \frac{1}{2}\left( {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right)\).
Cách giải:
Vì M là trung điểm của BC nên
\(\begin{array}{*{20}{l}}{\overrightarrow {AM} {\rm{ \;}} = \frac{1}{2}\left( {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right)}\\{ \Leftrightarrow 2\overrightarrow {AM} {\rm{ \;}} = \overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} }\\{ \Leftrightarrow \overrightarrow {AC} {\rm{ \;}} = {\rm{ \;}} – \overrightarrow {AB} {\rm{ \;}} + 2\overrightarrow {AM} }\\{ \Rightarrow x = {\rm{ \;}} – 1,{\mkern 1mu} {\mkern 1mu} y = 2.}\end{array}\)
Vậy cặp số (x;y) cần tìm là (-1;2).
Chọn C.
Câu 4 (TH):
Phương pháp:
Tính số HS thích học một trong hai môn.
Tính số HS thích học cả hai môn = Số HS thích môn Văn + số HS thích môn Toán – số HS thích một trong hai môn.
Cách giải:
Số học sinh thích môn Văn hoặc Toán là: 37 – 9 = 28 (bạn).
Số học sinh thích cả hai môn Văn và Toán là: (17 + 19) – 28 = 8 (bạn).
Chọn B.
Câu 5 (TH):
Phương pháp:
Giải từng bất phương trình.
Lấy giao hai tập hợp nghiệm của hai bất phương trình.
Cách giải:
Giải từng bất phương trình:
\(3x – 4 \ge 0 \Leftrightarrow x \ge \frac{4}{3} \Rightarrow {S_1} = \left[ {\frac{4}{3}; + \infty } \right)\).
\(\frac{{x – 1}}{2} – x \ge {\rm{ \;}} – 2 \Leftrightarrow x – 1 – 2x \ge {\rm{ \;}} – 2x \Leftrightarrow x \ge 1 \Rightarrow {S_2} = \left[ {1; + \infty } \right).\).
Vậy tập nghiệm của bất phương trình là \(S = {S_1} \cap {S_2} = \left[ {\frac{4}{3}; + \infty } \right).\)
Chọn C.
Câu 6 (TH):
Phương pháp:
Dựa vào các điểm thuộc miền nghiệm của bất phương trình.
Cách giải:
Thay tọa độ điểm (2;0) vào bất phương trình ta có: \(\left\{ {\begin{array}{*{20}{l}}{0 + 2 – 1 > 0}\\{2 \ge 2}\\{ – 0 + 2.2 > 3}\end{array}} \right.\) (đúng) nên điểm (0;2) thuộc miền nghiệm của hệ bất phương trình đã cho.
Dựa vào các đáp án ta thấy chỉ có đáp án C thỏa mãn.
Chọn C.
Câu 7 (VD):
Phương pháp:
Áp dụng định lí cosin trong tam giác ABC tính BC: \(B{C^2} = A{B^2} + A{C^2} – 2AB.AC.\cos A\).
Sử dụng công thức tính diện tích tam giác: \({S_{ABC}} = \frac{1}{2}AB.AC.\sin A.\)
Sử dụng công thức \({S_{ABC}} = \frac{{AB.AC.BC}}{{4R}}\), từ đó suy ra R.
Cách giải:
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{B{C^2} = A{B^2} + A{C^2} – 2AB.AC.\cos A}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {9^2} + {{18}^2} – 2.9.8.\cos {{60}^0} = 243}\\{ \Rightarrow BC = 9\sqrt 3 }\end{array}\)
Khi đó ta có: \({S_{ABC}} = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.9.18.\sin {60^0} = \frac{{81\sqrt 3 }}{2}\).
Mà \({S_{ABC}} = \frac{{AB.AC.BC}}{{4R}} \Rightarrow R = \frac{{AB.AC.BC}}{{4{S_{ABC}}}} = \frac{{9.18.9\sqrt 3 }}{{4.\frac{{81\sqrt 3 }}{2}}} = 9.\)
Chọn C.
Câu 8 (TH):
Phương pháp:
Sử dụng định lí Sin trong tam giác ABC ta có: \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\).
Cách giải:
Xét tam giác ABC ta có: C = 1800 – (A + B) = 750.
Sử dụng định lí Sin trong tam giác ABC ta có: \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\).
\( \Rightarrow AC = \frac{{AB}}{{\sin C}}.\sin B = \frac{8}{{\sin {{75}^0}}}.\sin {45^0} \approx 5,86.\)
Chọn B.
Câu 9 (TH):
Phương pháp:
Sử dụng \({\sin ^2}x + {\cos ^2}x = 1,{\mkern 1mu} {\mkern 1mu} \tan x = \frac{{\sin x}}{{\cos x}}\).
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{{{\tan }^2}x{{\sin }^2}x – {{\tan }^2}x + {{\sin }^2}x}\\{ = {{\tan }^2}x\left( {{{\sin }^2}x – 1} \right) + {{\sin }^2}x}\\{ = \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}}.\left( { – {{\cos }^2}x} \right) + {{\sin }^2}x}\\{ = {\rm{ \;}} – {{\sin }^2}x + {{\sin }^2}x = 0.}\end{array}\)
Chọn B.
Câu 10 (VD):
Phương pháp:
Sử dụng quy tắc ba điểm, phép nhân vectơ với một số.
Cách giải:
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \overrightarrow {AB} = 2\overrightarrow {AM} = 2\left( {\overrightarrow {AN} + \overrightarrow {NC} + \overrightarrow {CM} } \right)}\\{ \Leftrightarrow \overrightarrow {AB} = 2\overrightarrow {AN} + \overrightarrow {BC} + 2\overrightarrow {CM} }\\{ \Leftrightarrow \overrightarrow {AB} = 2\overrightarrow {AN} + 2\overrightarrow {CM} + \left( {\overrightarrow {BM} – \overrightarrow {CM} } \right)}\\{ \Leftrightarrow \overrightarrow {AB} = 2\overrightarrow {AN} + 2\overrightarrow {CM} – \frac{1}{2}\overrightarrow {AB} – \overrightarrow {CM} }\\{ \Leftrightarrow \frac{3}{2}\overrightarrow {AB} = 2\overrightarrow {AN} + \overrightarrow {CM} }\\{ \Leftrightarrow \overrightarrow {AB} = \frac{4}{3}\overrightarrow {AN} + \frac{2}{3}\overrightarrow {CM} }\end{array}\)
Chọn D.
Câu 11 (VD):
Phương pháp:
Áp dụng công thức tìm độ lệch chuẩn.
Cách giải:
Bảng phân bố tần số:
Điểm trung bình: \(\bar x = \frac{{45.4 + 55.6 + 65.10 + 75.6 + 85.4 + 95.2}}{{32}} = 66,875\) (điểm)
Phương sai: \({s^2} = \frac{1}{{32}}\left[ {4.{{\left( {45 – 66,875} \right)}^2} + 6.{{\left( {55 – 66,875} \right)}^2} + {\rm{\;}} \ldots {\rm{\;}} + 2.{{\left( {95 – 66,875} \right)}^2}} \right] \approx 190,234\) (điểm)
Độ lệch chuẩn: \(s = \sqrt[{}]{{{s^2}}} = \sqrt[{}]{{190,234}} \approx 13,793\) (điểm)
Chọn A.
Câu 12 (TH):
Phương pháp:
Cho tam giác ABC trọng tâm G và điểm M bất kì, ta có \(\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = 3\overrightarrow {MG} .\)
Cách giải:
Theo bài ra ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} + 4\overrightarrow {MC} {\rm{ \;}} = \vec 0}\\{ \Leftrightarrow \left( {\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} } \right) + 3\overrightarrow {MC} {\rm{ \;}} = \vec 0}\\{ \Leftrightarrow 3\overrightarrow {MG} {\rm{ \;}} + 3\overrightarrow {MC} {\rm{ \;}} = \vec 0}\\{ \Leftrightarrow \overrightarrow {MG} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0}\end{array}\)
=> M là trung điểm của GC.
Vậy M thuộc miền 1.
Chọn A.
Câu 13 (TH):
Phương pháp:
Sử dụng quy tắc hiệu.
Cách giải:
Theo bài ra ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {DB} {\rm{ \;}} = m\overrightarrow {DC} {\rm{ \;}} + \overrightarrow {DA} {\mkern 1mu} {\mkern 1mu} \left( {m > 0} \right)}\\{ \Leftrightarrow \overrightarrow {DB} {\rm{ \;}} – \overrightarrow {DA} {\rm{ \;}} = m\overrightarrow {DC} {\mkern 1mu} {\mkern 1mu} \left( {m > 0} \right)}\\{ \Leftrightarrow \overrightarrow {AB} {\rm{ \;}} = m\overrightarrow {DC} {\mkern 1mu} {\mkern 1mu} \left( {m > 0} \right)}\end{array}\)
Khi đó \(\overrightarrow {AB} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {DC} \) là hai vectơ cùng hướng.
Vậy ABCD là hình thang.
Chọn A.
Câu 14 (TH):
Phương pháp:
Sử dụng định lí Sin trong tam giác: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\).
Cách giải:
Sử dụng định lí Sin trong tam giác ta có:
\(\begin{array}{*{20}{l}}{\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = \frac{{b\sin A}}{{\sin B}}}\\{\sin c = \frac{{c\sin A}}{a}}\\{a = 2R\sin A}\end{array}} \right.}\end{array}\)
Suy ra A, C, D đúng.
Chọn B.
Câu 15 (NB):
Phương pháp:
Sử dụng ý nghĩa của phương sai và độ lệch chuẩn.
Cách giải:
Để đo độ phân tán (độ chênh lệch) giữa các giá trị của mẫu số liệu so với số trung bình, người ta sử dụng số đặc trưng là phương sai và độ lệch chuẩn.
Chọn C.
Câu 16 (TH):
Phương pháp:
Đối với bảng phân bố tần số, phương sai được tính theo công thức:
\({s^2} = \frac{1}{N}\left[ {{n_1}{{\left( {{x_1} – \bar x} \right)}^2} + {n_2}{{\left( {{x_2} – \bar x} \right)}^2} + {\rm{\;}} \ldots {\rm{\;}} + {n_k}{{\left( {{x_k} – \bar x} \right)}^2}} \right]\)
Với \({n_i};{\mkern 1mu} {\mkern 1mu} {f_i}\) lần lượt là tần số, tần suất của giá trị \({x_i}\).
Cách giải:
Bảng phân số tần số:

*) Sản lượng trung bình của 40 thửa ruộng là:
\(\bar x = \frac{{20.5 + 21.8 + 22.11 + 23.10 + 24.6}}{{40}} = 22,1{\mkern 1mu} \)(tạ)
*) Phương sai:
\({s^2} = \frac{1}{{40}}\left[ {5.{{\left( {20 – 22,1} \right)}^2} + 8.{{\left( {21 – 22,1} \right)}^2} + 11.{{\left( {22 – 22,1} \right)}^2} + 10.{{\left( {23 – 22,1} \right)}^2} + 6.{{\left( {24 – 22,1} \right)}^2}} \right]\)\( = 1,54\) (tạ)
Chọn B.
Câu 17 (NB):
Phương pháp:
Liệt kê các số tự nhiên nhỏ hơn 5.
Cách giải:
\(A = \left\{ {x \in \mathbb{N}|x < 5} \right\} = \left\{ {0,1,2,3,4,5} \right\}\).
Chọn C.
Câu 18 (NB):
Phương pháp:
\({C_X}Y = X\backslash Y = \{ x \in X\) và \(x \notin Y\} .\)
Cách giải:
Ta có: \({C_X}Y = X\backslash Y = \left\{ {3;4} \right\}.\)
Chọn A.
Câu 19 (NB):
Phương pháp:
Dựa vào các điểm thuộc miền nghiệm của hệ bất phương trình.
Cách giải:
Điểm (1;0) thuộc miền nghiệm của hệ bất phương trình nên loại đáp án A và D vì 1 – 0 < 0 (vô lý).
Điểm (1;0) thuộc miền nghiệm của hệ bất phương trình nên loại đáp án B vì 2.1 – 0 < 1 (vô lý).
Chọn C.
Câu 20 (TH):
Phương pháp:
Thay trực tiếp tọa độ các điểm ở các đáp án vào hệ bất phương trình.
Cách giải:
Thay tọa độ điểm A(0;1) vào bất phương trình: \(\left\{ {\begin{array}{*{20}{l}}{0 + 3.1 – 2 \ge 0}\\{2.0 + 1 + 1 \le 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{1 \ge 0}\\{2 \le 0}\end{array}} \right.\) (sai)
Thay tọa độ điểm C(1;3) vào bất phương trình: \(\left\{ {\begin{array}{*{20}{l}}{1 + 3.3 – 2 \ge 0}\\{2.1 + 3 + 1 \le 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{8 \ge 0}\\{6 \le 0}\end{array}} \right.\) (sai)
Thay tọa độ điểm B(-1;1) vào bất phương trình: \(\left\{ {\begin{array}{*{20}{l}}{ – 1 + 3.1 – 2 \ge 0}\\{2\left( { – 1} \right) + 1 + 1 \le 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{0 \ge 0}\\{0 \le 0}\end{array}} \right.\) (đúng)
Thay tọa độ điểm D(-1;0) vào bất phương trình: \(\left\{ {\begin{array}{*{20}{l}}{ – 1 + 3.0 – 2 \ge 0}\\{2\left( { – 1} \right) + 0 + 1 \le 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ – 3 \ge 0}\\{ – 1 \le 0}\end{array}} \right.\) (sai)
Vậy điểm B(-1;1) thuộc miền nghiệm của hệ bất phương trình.
Chọn C.
Câu 21 (TH):
Phương pháp:
Sử dụng công thức \({\sin ^2}x + {\cos ^2}x = 1\) tính \(\cos x.\)
Tính \(\tan x = \frac{{\sin x}}{{\cos x}}\).
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{{{\sin }^2}x + {{\cos }^2}x = 1}\\{ \Leftrightarrow {{\left( {\frac{3}{5}} \right)}^2} + {{\cos }^2}x = 1}\\{ \Leftrightarrow {{\cos }^2}x = \frac{{16}}{{25}}}\\{ \Leftrightarrow \cos x = {\rm{ \;}} \pm \frac{4}{5}}\end{array}\)
Vì \({90^0} < x < {180^0} \Rightarrow \cos x < 0\).
\( \Rightarrow \cos x = {\rm{ \;}} – \frac{4}{5} \Rightarrow \tan x = \frac{{\sin x}}{{\cos x}} = \frac{{\frac{3}{5}}}{{ – \frac{4}{5}}} = {\rm{ \;}} – \frac{3}{4}\).
Vậy \(P = \tan x.{\cos ^2}x = {\rm{ \;}} – \frac{3}{4}.\frac{{16}}{{25}} = {\rm{ \;}} – \frac{{12}}{{25}}.\)
Chọn D.
Câu 22 (VD):
Phương pháp:
Chia cả tử và mẫu biểu thức P cho \cos \alpha và biểu diễn biểu thức P theo \tan \alpha .
Cách giải:
Vì \(\tan \alpha {\rm{ \;}} = {\rm{ \;}} – 2\) xác định nên \(\cos \alpha {\rm{ \;}} \ne 0.\)
Chia cả tử và mẫu của biểu thức P cho \(\cos \alpha \) ta được:
\(\begin{array}{*{20}{l}}{P = \frac{{2\sin \alpha {\rm{ \;}} + 3\cos \alpha }}{{3\sin \alpha {\rm{ \;}} – 2\cos \alpha }} = \frac{{2\frac{{\sin \alpha }}{{\cos \alpha }} + 3}}{{3\frac{{\sin \alpha }}{{\cos \alpha }} – 2}}}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{{2\tan \alpha {\rm{ \;}} + 3}}{{3\tan \alpha {\rm{ \;}} – 2}} = \frac{{2.\left( { – 2} \right) + 3}}{{3.\left( { – 2} \right) – 2}} = \frac{{ – 1}}{{ – 8}} = \frac{1}{8}.}\end{array}\)
Chọn D.
Câu 23 (TH):
Phương pháp:
Áp dụng quy tắc cộng vecto, quy tắc hình bình hành để biểu diễn véctơ.
Cách giải:
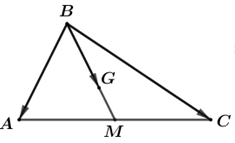
\(\overrightarrow {BM} {\rm{\;}} = \frac{1}{2}\left( {\overrightarrow {BA} {\rm{\;}} + \overrightarrow {BC} } \right) = \frac{1}{2}\overrightarrow {BA} {\rm{\;}} + \frac{1}{2}\overrightarrow {BC} \)
\( \Rightarrow \overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\overrightarrow {BM} {\rm{\;}} = \frac{2}{3} \cdot \left( {\frac{1}{2}\overrightarrow {BA} {\rm{\;}} + \frac{1}{2}\overrightarrow {BC} } \right) = \frac{1}{3}\overrightarrow {BA} {\rm{\;}} + \frac{1}{3}\overrightarrow {BC} \)
Mặt khác, \(\overrightarrow {BA} {\rm{\;}} = \vec a,{\mkern 1mu} {\mkern 1mu} \overrightarrow {BC} {\rm{\;}} = \vec b\) nên ta có: \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\)
Vậy \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\).
Chọn A.
Câu 24 (NB):
Phương pháp:
Áp dụng điều kiện để hai vecto cùng phương. Điều kiện cần và đủ để ba điểm thẳng hàng.
Cách giải:
Theo lý thuyết, ba điểm \(A,{\mkern 1mu} {\mkern 1mu} B,{\mkern 1mu} {\mkern 1mu} C\) phân biệt thẳng hàng khi và chỉ khi tồn tại \(k\) khác \(0\) sao cho \(\overrightarrow {AB} {\rm{\;}} = k\overrightarrow {AC} \).
Do vậy, khẳng định sai là: Ba điểm phân biệt \(A,B,C\) thẳng hàng khi và chỉ khi \(\overrightarrow {AB} {\rm{\; = \;}}k\overrightarrow {AC} \).
Vì xảy ra trường hợp \(k = 0\), khi đó \(\overrightarrow {AB} {\rm{\;}} = k\overrightarrow {AC} {\rm{\;}} = 0.\overrightarrow {AC} {\rm{\;}} = 0\) (vô lý)
Chọn D.
Câu 25 (NB):
Phương pháp:
Dùng công thức diện tích \(S = pr = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} \)
Cách giải:
\(\begin{array}{*{20}{l}}{S = pr = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} }\\{ \Rightarrow r = \frac{{\sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} }}{p} = 1,63}\end{array}\)
với \(p = \frac{{a + b + c}}{2} = 9\)
Chọn A.
Câu 26 (TH):
Phương pháp:
Tính sai số tương đối \({\delta _a} = \frac{{{\Delta _a}}}{{\left| a \right|}} \le \frac{d}{{\left| a \right|}}\) trong mỗi đáp án. Sai số tương đối càng nhỏ thì kết quả đo được càng chính xác.
Cách giải:
Đáp án A: \({\delta _a} \le \frac{{0,01}}{{15,34}} = 0,00065189…\)
Đáp án B: \({\delta _b} \le \frac{{0,2}}{{127,4}} = 0,00156985…\)
Đáp án C: \({\delta _c} \le \frac{{0,5}}{{2135,8}} = 0,00023410…\)
Đáp án D: \({\delta _d} \le \frac{{0,15}}{{63,47}} = 0,00236332…\)
Ta thấy \({\delta _c}\) là nhỏ nhất trong các số trên. Vậy phép đo trong ý C có kết quả chính xác nhât.
Chọn C.
Câu 27 (TH):
Phương pháp:
Khoảng tứ phân vị, kí hiệu là \({\Delta _Q}\), là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất, tức là: \({\Delta _Q} = {Q_3} – {Q_1}\)
Cách giải:
Cỡ mẫu là n = 10 chẵn nên giá trị tứ phân vị thứ hai là \({Q_2} = \frac{1}{2}\left( {2 + 2} \right) = 2\).
Tứ phân vị thứ nhất là trung vị của mẫu 1 1 1 2 2 . Do đó \({Q_1} = 1\).
Tứ phân vị thứ ba là trung vị của mẫu 2 3 3 4 20. Do đó \({Q_3} = 3\).
Vậy khoảng biến thiên của mẫu số liệu là: \({\Delta _Q} = {Q_3} – {Q_1} = 3 – 1 = 2.\)
Chọn A.
Câu 28 (TH):
Phương pháp:
Giá trị gần đúng tốt nhất khi sai số tuyệt đối nhỏ nhất.
Cách giải:
Đáp án A: \({\Delta _A} = \left| {\frac{2}{7} – 0,28} \right| = 0,0057\).
Đáp án B: \({\Delta _B} = \left| {\frac{2}{7} – 0,29} \right| = 0,0042\)
Đáp án C: \({\Delta _C} = \left| {\frac{2}{7} – 0,286} \right| = 0,00028\)
Đáp án D: \({\Delta _D} = \left| {\frac{2}{7} – 0,287} \right| = 0,00128\)
Vậy số gần đúng 0,286 là tốt nhất.
Chọn C.
Câu 29 (TH):
Phương pháp:
Sử dụng quy tắc hình bình hành.
Sử dụng: hai vectơ vuông góc với nhau thì tích vô hướng bằng 0.
Cách giải:
Lấy D sao cho ACBD là hình bình hành, khi đó ta có: \(\overrightarrow {CA} {\rm{ \;}} + \overrightarrow {CB} {\rm{ \;}} = \overrightarrow {CD} \).
Theo bài ra ta có: \(\left( {\overrightarrow {CA} {\rm{ \;}} + \overrightarrow {CB} } \right).\overrightarrow {AB} {\rm{ \;}} = 0 \Leftrightarrow \overrightarrow {CD} .\overrightarrow {AB} {\rm{ \;}} = 0\) \( \Rightarrow CD \bot AB\).
Hình bình hành ACBD có hai đường chéo vuông góc nên là hình thoi, do đó CA = CB.
Vậy tam giác ABC cân tại C.
Chọn B.
Câu 30 (NB):
Phương pháp:
Sử dụng định nghĩa tích vô hướng của hai vectơ: \(\vec a.\vec b{\rm{ \;}} = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\).
Cách giải:
Vì tam giác ABC vuông cân tại A nên \(AB \bot AC\).
Vậy \(\overrightarrow {AB} .\overrightarrow {AC} {\rm{ \;}} = 0.\)
Chọn C.
Phần 2: Tự luận (4 điểm)
Câu 1 (VD):
Phương pháp:
a)
* Số trung bình của mẫu số liệu \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2},{\mkern 1mu} {\mkern 1mu} ….,{\mkern 1mu} {\mkern 1mu} {x_n}\) kí hiệu là \(\bar x\), được tính bằng công thức:
\(\bar x = \frac{{{m_1}{x_2} + {m_2}{x_2} + … + {m_k}{x_k}}}{n}\)
Trong đó mk là tần số của giá trị xk và \(n = {m_1} + {m_2} + … + {m_k}\).
* Tứ phân vị của mẫu số liệu:
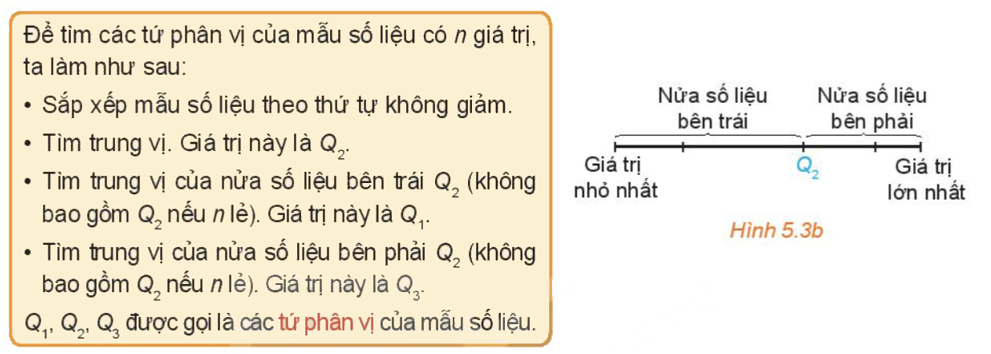
* Mốt của mẫu số liệu là giá trị xuất hiện với tần số lớn nhất.
b) Tìm trung vị của mẫu số liệu.
Để tìm trung vị của mẫu số liệu, ta thực hiện như sau:
– Sắp xếp các giá trị trong mẫu số liệu theo thứ tự không giảm.
– Nếu giá trị của mẫu số liệu là số lẻ thì giá trị chính giữa của mẫu là trung vị. Nếu là số chẵn thì trung vị là trung bình cộng của hai giá trị chính giữa của mẫu.
So sánh số trung bình và trung vị của hai năm.
Cách giải:
a)
* Số trung bình của thời gian thi nghề của các thí sinh là:
\(\bar x = \frac{{5.1 + 6.3 + 7.5 + 8.2 + 35.1}}{{1 + 3 + 5 + 2 + 1}} = \frac{{109}}{{12}} \approx 9,08\) (phút)
* Tìm tứ phân vị:
Sắp xếp mẫu số liệu theo thứ tự không giảm ta được: 5 6 6 6 7 7 7 7 7 8 8 35
Vì cỡ mẫu là n = 12 chẵn nên giá trị tứ phân vị thứ hai là \({Q_2} = \frac{1}{2}\left( {7 + 7} \right) = 7.\)
Tứ phân vị thứ nhất là trung vị của mẫu 5 6 6 6 7 7. Do đó \({Q_1} = \frac{1}{2}\left( {6 + 6} \right) = 6\).
Tứ phân vị thứ ba là trung vị của mẫu 7 7 7 8 8 35. Do đó \({Q_3} = \frac{1}{2}\left( {7 + 8} \right) = 7,5\).
* Số thí sinh có thời gian hoàn thành 1 sản phẩm trong vòng 7 phút là lớn nhất (có 5 người) nên mốt là 7.
b) Số trung vị của mẫu số liệu là \({M_e} = {Q_2} = 7.\)
Ta thấy: Số trung bình của năm ngoái thấp hơn năm nay, tuy nhiên giá trị số trung vị hai năm đều bằng 7, do đó xét về mặt bằng chung, thời gian thi trung bình hai năm là tương đương nhau.
Câu 2 (VD):
Phương pháp:
Gọi I là trung điểm của AB, J là điểm nằm trên đường thẳng AC thỏa mãn điều kiện \(\overrightarrow {JA} = 3\overrightarrow {JC} \)\( \Leftrightarrow \overrightarrow {JA} – 3\overrightarrow {JC} = \vec 0\)
Đưa đẳng thức đã cho về dạng MI = MJ, sử dụng công thức trung điểm, quy tắc ba điểm. Từ đó suy ra tập hợp điểm M.
Cách giải:

Gọi I là trung điểm của AB, J là điểm nằm trên đường thẳng AC thỏa mãn điều kiện \(\overrightarrow {JA} = 3\overrightarrow {JC} \)\( \Leftrightarrow \overrightarrow {JA} – 3\overrightarrow {JC} = \vec 0\)
Khi đó ta có:
\(\begin{array}{*{20}{l}}{\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA} – 3\overrightarrow {MC} } \right|}\\{ \Leftrightarrow \left| {2\overrightarrow {MI} } \right| = \left| {\overrightarrow {MJ} + \overrightarrow {JA} – 3\left( {\overrightarrow {MJ} + \overrightarrow {JC} } \right)} \right|}\\{ \Leftrightarrow \left| {2\overrightarrow {MI} } \right| = \left| { – 2\overrightarrow {MJ} + \left( {\overrightarrow {JA} – 3\overrightarrow {JC} } \right)} \right|}\\{ \Leftrightarrow \left| {2\overrightarrow {MI} } \right| = \left| { – 2\overrightarrow {MJ} } \right|}\\{ \Leftrightarrow MI = MJ}\end{array}\)
Vậy tập hợp các điểm M là đường trung trực của IJ.
Câu 3 (VDC):
Phương pháp:
Sử dụng \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} + \overrightarrow {CA} {\rm{ \;}} = \vec 0\), bình phương hai vế, sử dụng khái niệm tích vô hướng của 2 vectơ.
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \vec 0}\\{ \Rightarrow {{\left( {\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} } \right)}^2} = 0}\\{ \Leftrightarrow {{\overrightarrow {AB} }^2} + {{\overrightarrow {BC} }^2} + {{\overrightarrow {CA} }^2} + 2\overrightarrow {AB} .\overrightarrow {BC} + 2\overrightarrow {BC} .\overrightarrow {CA} + 2\overrightarrow {CA} .\overrightarrow {AB} = 0}\\{ \Leftrightarrow {a^2} + {b^2} + {c^2} = 2\overrightarrow {BA} .\overrightarrow {BC} + 2\overrightarrow {CB} .\overrightarrow {CA} + 2\overrightarrow {AC} .\overrightarrow {AC} }\\{ \Leftrightarrow {a^2} + {b^2} + {c^2} = 2ac\cos B + 2bc\cos A + 2ab\cos C}\\{ \Leftrightarrow \frac{{{a^2} + {b^2} + {c^2}}}{{2abc}} = \frac{{\cos A}}{a} + \frac{{\cos B}}{b} + \frac{{\cos C}}{c}{\mkern 1mu} \left( {dpcm} \right).}\end{array}\)
Mặt khác, theo định lí cosin trong tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{{a^2} = {b^2} + {c^2} – 2bc\cos A}\\{ \Leftrightarrow {a^2} = 5{a^2} – 2bc\cos A}\\{ \Leftrightarrow 2bc\cos A = 4{a^2}}\\{ \Leftrightarrow bc = \frac{{2{a^2}}}{{\cos A}} = \frac{{2{a^2}}}{{\cos \alpha }}}\end{array}\)
Vậy \({S_{\Delta ABC}} = \frac{1}{2}bc\sin A = \frac{1}{2}\frac{{2{a^2}}}{{2\cos \alpha }}\sin \alpha {\rm{ \;}} = {a^2}\tan \alpha .\)
Đề 4
Phần 1: Trắc nghiệm (30 câu – 6 điểm)
Câu 1: Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Hãy đi nhanh lên! b) Hà Nội là thủ đô của Việt Nam.
c) \(5 + 7 + 4 = 15\) d) Năm 2018 là năm nhuận.
A. 1 B. 2 C. 3 D. 4
Câu 2: Cho số gần đúng a = 23748023 với độ chính xác d = 123. Hãy viết số quy tròn của số a.
A. 23749000. B. 23748000. C. 23746000. D. 23737000.
Câu 3: Cho tam giác ABC và điểm \(M\) thỏa mãn điều kiện \(\overrightarrow {MA} {\rm{ \;}} – \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\). Mệnh đề nào sau đây sai?
A. MABC là hình bình hành. B. \(\overrightarrow {AM} {\rm{ \;}} + \overrightarrow {AB} {\rm{ \;}} = \overrightarrow {AC} \)
C. \(\overrightarrow {BA} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} = \overrightarrow {BM} \) D. \(\overrightarrow {MA} {\rm{ \;}} = \overrightarrow {BC} \)
Câu 4: Cho tam giác ABC có \(AB = \sqrt 5 ,{\mkern 1mu} {\mkern 1mu} AC = \sqrt 2 \) và \(\angle C = {45^0}\). Tính độ dài cạnh BC.
A. \(3\) B. \(2\) C. \(\sqrt 3 \) D. \(\sqrt 2 \)
Câu 5: Cặp số (x;y) nào là sau đây là một nghiệm của bất phương trình \(x–2y + 5 > 0\).
A. (x;y) = (0;4). B. (x;y) = (2;5). C. (x;y) = (2;3). D. (x;y) = (1;4).
Câu 6: Cho tam giác ABC và điểm \(M\) thỏa mãn điều kiện \(\overrightarrow {MA} {\rm{ \;}} – \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\). Mệnh đề nào sau đây sai?
A. MABC là hình bình hành. B. \(\overrightarrow {AM} {\rm{ \;}} + \overrightarrow {AB} {\rm{ \;}} = \overrightarrow {AC} \)
C. \(\overrightarrow {BA} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} = \overrightarrow {BM} \) D. \(\overrightarrow {MA} {\rm{ \;}} = \overrightarrow {BC} \)
Câu 7: Tam giác ABC có \(\angle A = {45^0},{\mkern 1mu} {\mkern 1mu} c = 6,{\mkern 1mu} {\mkern 1mu} \angle B = {75^0}\). Độ dài bán kính đường tròn ngoại tiếp tam giác bằng:
A. \(8\sqrt 3 \) B. \(2\sqrt 3 \) C. \(6\sqrt 3 \) D. \(4\sqrt 3 \)
Câu 8: Cho tam giác ABC với ba cạnh a, b, c. Khi đó \(\frac{{\cos A}}{a} + \frac{{\cos B}}{b} + \frac{{\cos C}}{c}\) bằng
A. \(\frac{{{a^2} + {b^2} + {c^2}}}{{2abc}}\) B. \(\frac{{{a^2} + {b^2} + {c^2}}}{{abc}}\) C. \(\frac{{2\left( {{a^2} + {b^2} + {c^2}} \right)}}{{abc}}\) D. \(\frac{{{a^2} + {b^2} + {c^2}}}{{4abc}}\)
Câu 9: Cho hai tập hợp: \(A = \left\{ {x \in \mathbb{R}|{x^2} – 7x + 6 = 0} \right\}\)và \(B = \left\{ {x \in \mathbb{R}|\left| x \right| > 4} \right\}\). Khẳng định nào sau đây đúng?
A. \(A \cup B = A\) B. \(A \cap B = A \cup B\) C. \(\left( {A\backslash B} \right) \subset A\) D. \(B\backslash A = \emptyset \)
Câu 10: Cho các tập hợp A, B, C được minh họa bằng biểu đồ Ven như hình vẽ. Phần tô màu xám trong hình là biểu diễn của tập hợp nào sau đây?
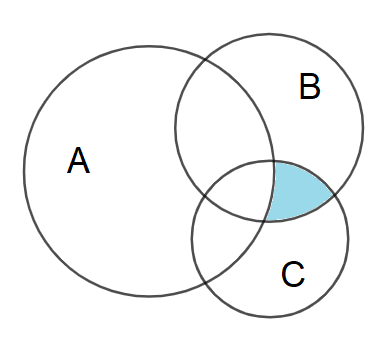
A. \(A \cap B \cap C.\) B. \(\left( {A\backslash C} \right) \cup \left( {A\backslash B} \right).\) C. \(\left( {B \cup C} \right)\backslash A.\) D. \(\left( {B \cap C} \right)\backslash A.\)
Câu 11: Để xác định chiều cao của một toà nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh toà nhà với góc nâng \(\angle RQA = {79^0}\), người đó lùi ra xa một khoảng cách LM = 50 m thì nhìn thấy đỉnh toà nhà với góc nâng \(\angle RPA = {65^0}\). Hãy tính chiều cao của toà nhà (làm tròn đến chữ số thập phân thứ nhất), biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là PL = QM = 1,4m.
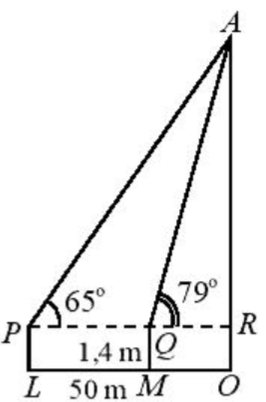
A. 135,8m B. 183,5m C. 158,3m D. 185,3m
Câu 12: Biết \(\sin x = \frac{1}{{\sqrt 3 }}\). Giá trị của biểu thức \(P = 2{\sin ^2}x – {\cos ^2}x\) là
A. \( – \frac{4}{3}\) B. \(0\) C. \(\frac{4}{3}\) D. \(\frac{2}{3}\)
Câu 13: Cho hai tập hợp: \(A = \left\{ {x \in \mathbb{R}|\left( {2{x^2} – 7x + 5} \right)\left( {x – 2} \right) = 0} \right\}\) và \(B = \left\{ {x \in \mathbb{Z}| – 3 < 2x + 1 < 5} \right\}\)
Kết luận nào sau đây là đúng?
A. \(A \cap B = \left\{ { – 1;{\mkern 1mu} {\mkern 1mu} \frac{5}{2};{\mkern 1mu} {\mkern 1mu} 2} \right\}\) B. \(A \cap B = \left\{ 1 \right\}\) C. \(A \cap B = \left\{ { – 1;{\mkern 1mu} {\mkern 1mu} 0;{\mkern 1mu} {\mkern 1mu} 2;{\mkern 1mu} {\mkern 1mu} \frac{5}{2};{\mkern 1mu} {\mkern 1mu} 2} \right\}\) D. \(A \cap B = \left\{ { – 1;{\mkern 1mu} {\mkern 1mu} 0;{\mkern 1mu} {\mkern 1mu} 1} \right\}\)
Câu 14: Cho \(\cos \alpha {\rm{ \;}} = \frac{1}{4}\). Giá trị của \(P = \frac{{\tan \alpha {\rm{ \;}} + 2\cot \alpha }}{{2\tan \alpha {\rm{ \;}} + 3\cot \alpha }}\) là:
A. \( – \frac{{17}}{{33}}\) B. \(\frac{{17}}{{33}}\) C. \(\frac{1}{2}\) D. \(\frac{{16}}{{33}}\)
Câu 15: Cho ba lực \(\overrightarrow {{F_1}} {\rm{ \;}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} {\rm{ \;}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} {\rm{ \;}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm \(M\) và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) đều bằng 50N và góc \(\widehat {AMB} = {60^^\circ }\). Khi đó cường độ lực \(\overrightarrow {{F_1}} \) của là
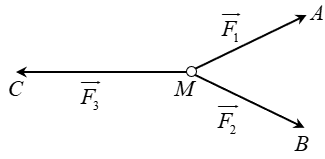
A. \(100\sqrt 3 N\) B. \(25\sqrt 3 N\) C. \(50\sqrt 3 N\) D. \(50\sqrt 2 N\)
Câu 16: Cho ba véctơ bất kì \(\vec u,\vec v,\vec w\) bất kì. Mệnh đề nào sau đây đúng?
A. \(\left| {\vec u + \vec v + \vec w} \right| \ge \left| {\vec u} \right| + \left| {\vec v} \right| + \left| {\vec w} \right|\) B. \(\left| {\vec u + \vec v} \right| \le \left| {\vec u} \right| + \left| {\vec v} \right|\)
C. \(\left| {\vec u + \vec v + \vec w} \right| \ge \left| {\vec u} \right| – \left| {\vec v} \right| + \left| {\vec w} \right|\) D. \(\left| {\vec u + \vec v} \right| \le \left| {\vec u} \right| – \left| {\vec v} \right|\)
Câu 17: Người ta chọn một số bút bi của hai hãng sản xuất A và B thử xem sử dụng một bút thì sau bao nhiêu giờ thì hết mực. Kết quả như sau (đơn vị giờ):
Loại bút A: \(\begin{array}{*{20}{c}}{23}&{25}&{27}&{28}&{30}&{35}\end{array}\)
Loại bút B: \(\begin{array}{*{20}{c}}{16}&{22}&{28}&{33}&{46}\end{array}\)
Nhận xét nào sau đây là đúng?
A. Loại bút A có thời gian sử dụng lâu hơn và chất lượng của loại bút A không đồng đều.
B. Loại bút A có thời gian sử dụng lâu hơn và chất lượng của loại bút A đồng đều.
C. Loại bút B có thời gian sử dụng lâu hơn và chất lượng của loại bút B không đồng đều.
D. Loại bút B có thời gian sử dụng lâu hơn và chất lượng của loại bút B đồng đều.
Câu 18: Phương sai của một mẫu số liệu \(\left\{ {{x_1};{x_2};…;{x_N}} \right\}\) bằng
A. Hai lần độ lệch chuẩn. B. Căn bậc hai của độ lệch chuẩn.
C. \(\sum\limits_{i = 1}^N {{{\left( {{x_i} – \bar x} \right)}^2}} .\) D. Bình phương của độ lệch chuẩn.
Câu 19: Cho tam giác ABC vuông cân tại A có AB = 6. Giá trị của \(\overrightarrow {BA} .\overrightarrow {BC} \) bằng
A. 0. B. 36. C. -36. D. \(36\sqrt 2 .\)
Câu 20: Quan sát 9 con chuột chạy quanh một căn phòng và ghi lại thời gian (tính bằng phút) của chúng trong bảng sau:

Số trung vị và Mốt của mẫu số liệu thống kê trên lần lượt là
A. 5 và 9 B. 2 và 30 C. 1,5 và 1 D. 1,5 và 2
Câu 21: (ID: 590911) Đường thẳng \(2x – 3y + 6 = 0\) chia mặt phẳng tọa độ thành các miền như hình vẽ. Miền nghiệm của \(2x – 3y + 6 \ge 0\) là:
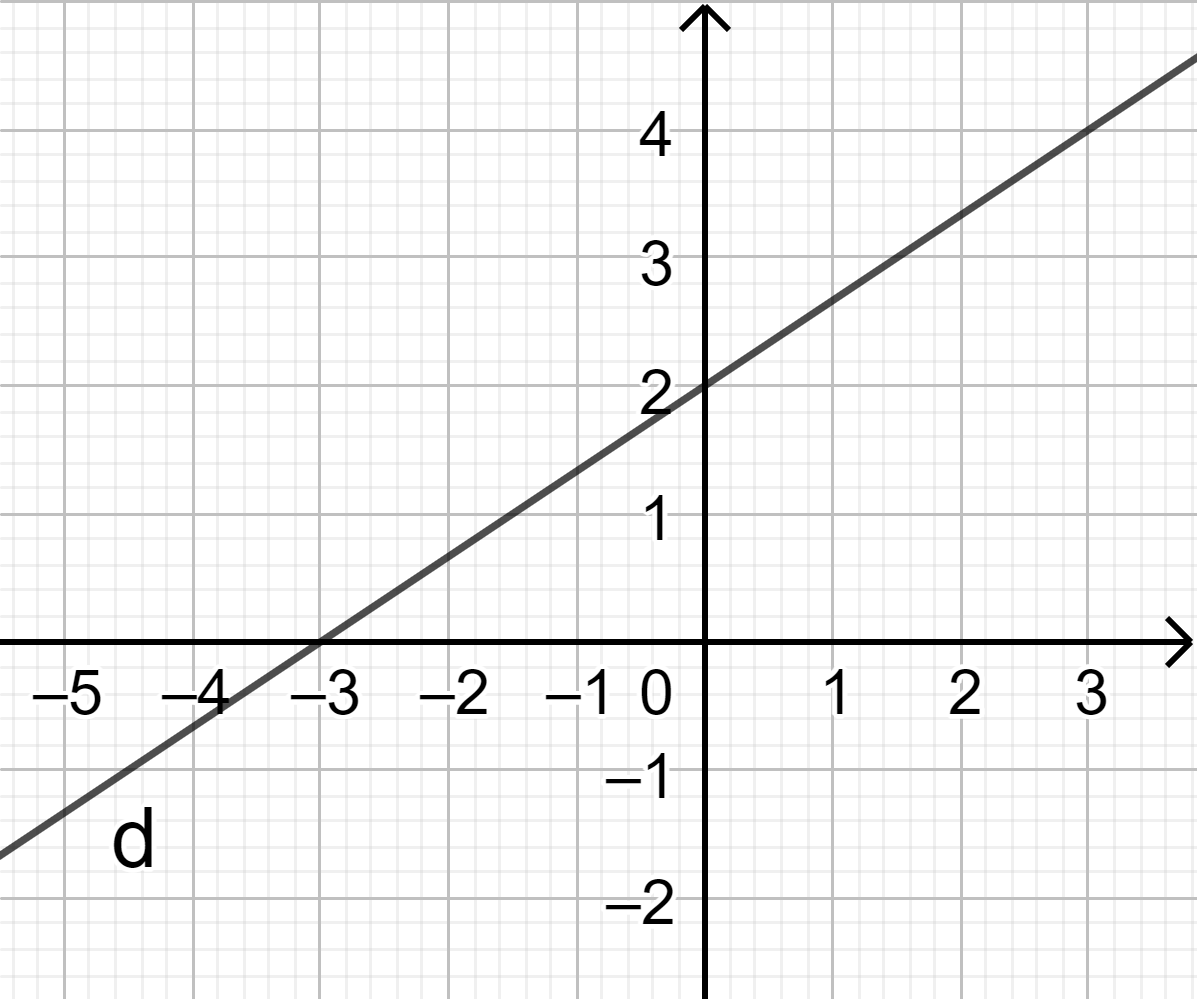
A. Nửa mặt phẳng bờ d chứa gốc tọa độ O và có lấy đường thẳng d.
B. Nửa mặt phẳng bờ d chứa gốc tọa độ O và có lấy đường thẳng d.
C. Nửa mặt phẳng bờ d không chứa gốc tọa độ O và không lấy đường thẳng d.
D. Nửa mặt phẳng bờ d không chứa gốc tọa độ O và không lấy đường thẳng d.
Câu 22: Điểm nào dưới đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 2y > – 3}\\{3x – y < 5}\\{y – 1 > 0}\end{array}} \right.\).
A. \(\left( { – 2; – 1} \right)\) B. \(\left( {2;0} \right)\) C. \(\left( {3;2} \right)\) D. \(\left( {0,2} \right)\)
Câu 23: Giá trị của biểu thức \(B = \cos {0^0} + \cos {20^0} + \cos {40^0} + … + \cos {160^0} + \cos {180^0}\) là
A. \(0\) B. \(1\) C. \( – 1\) D. \(\frac{1}{2}\)
Câu 24: Cho tam giác đều ABC có độ dài các cạnh bằng 6 và điểm M thỏa mãn \(\overrightarrow {BM} {\rm{ \;}} = {\rm{ \;}} – \frac{1}{3}\overrightarrow {BC} \). Tích vô hướng \(\overrightarrow {BM} .\overrightarrow {BA} \) bằng
A. \(6\) B. \( – 6\sqrt 3 .\) C. \(6\sqrt 3 .\) D. \( – 6.\)
Câu 25: Độ dài của cầu Bến Thủy 2 (Nghệ An) người ta đo được là \(996m \pm 0,5m\), có nghĩa là:
A. Độ dài đúng của cầu là một số nằm trong khoảng 995,5m đến 996,5m.
B. Độ dài đúng của cầu là một số lớn hơn 996m.
C. Độ dài đúng của cầu là một số nhỏ hơn 996m.
D. Độ dài đúng của cầu là 995,5m hoặc là 996,5m.
Câu 26: Hình chữ nhật có các cạnh \(x = 2m \pm 1cm,\,\,y = 5m \pm 2cm\). Diện tích hình chữ nhật và sai số tương đối của giá trị đó là:
A. 10m2 và 5 % B. 10m2 và 4 % C. 10m2 và 9 % D. 10m2 và 20%
Câu 27: Khoảng biến thiên của mẫu số liệu 13; 16; 9; 10; 5; 8; 11; 17; 6; 20 là:
A. 5. B. 8. C. 15. D. 20.
Câu 28: Trong đợt hội diễn văn nghệ chào mừng 20/11, lớp 10A đăng kí hai tiết mục là múa và diễn kịch. Trong danh sách, có 9 học sinh tham gia tiết mục múa, 13 học sinh tham gia diễn kịch; trong đó có 4 học sinh tham gia cả tiết mục múa và diễn kịch. Hỏi lớp 10A có tất cả bao nhiêu học sinh tham gia hội diễn văn nghệ?
A. 15. B. 18. C. 21. D. 26.
Câu 29: Cho hình vuông ABCD có cạnh bằng \(a\). Khi đó \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right|\) bằng:
A. \(\frac{{a\sqrt 5 }}{2}\) B. \(\frac{{a\sqrt 3 }}{2}\) C. \(\frac{{a\sqrt 3 }}{3}\) D. \(a\sqrt 5 \)
Câu 30: Cho hai vectơ \(\vec a\) và \(\vec b\) khác \(\vec 0\). Xác định góc \(\alpha \) giữa hai vectơ \(\vec a\) và \(\vec b\) khi \(2\vec a.\vec b{\rm{ \;}} = {\rm{ \;}}\left| {\vec a} \right|.\left| {\vec b} \right|\).
A. \(\alpha {\rm{ \;}} = {180^0}.\) B. \(\alpha {\rm{ \;}} = {120^0}.\) C. \(\alpha {\rm{ \;}} = {90^0}.\) D. \(\alpha {\rm{ \;}} = {60^0}.\)
Phần 2: Tự luận (4 điểm)
Câu 1: Cho tam giác ABC.
a) Tìm điểm K sao cho \(\overrightarrow {KA} {\rm{ \;}} + 2\overrightarrow {KB} {\rm{ \;}} = \overrightarrow {CB} \).
b) Tìm điểm M sao cho \(\overrightarrow {MA} {\rm{ \;}} + 2\overrightarrow {MB} {\rm{ \;}} + 2\overrightarrow {MC} {\rm{ \;}} = \vec 0\).
Câu 2: Kết quả dự báo nhiệt độ cao nhất trong 10 ngày liên tiếp ở Nghệ An cuối tháng 01 năm 2022 được cho ở bảng sau:

(Nguồn: https://nchmf.gov.vn)
a) Viết mẫu số liệu thống kê nhiệt độ nhận được từ bảng trên.
b) Tính số trung bình cộng, phương sai và độ lệch chuẩn của mẫu số liệu đó.
Câu 3: Chứng minh rằng với mọi tam giác ABC ta có
a) \(\cot A + \cot B + \cot C = \frac{{{a^2} + {b^2} + {c^2}}}{{abc}}R\)
b) \(\sin \frac{A}{2} = \sqrt {\frac{{(p – b)(p – c)}}{{bc}}} \)
—– HẾT —–
Giải đề 4
HƯỚNG DẪN GIẢI CHI TIẾT
THỰC HIỆN: BAN CHUYÊN MÔN LOIGIAIHAY.COM
Phần 1: Trắc nghiệm (30 câu – 6 điểm)
|
1.C
|
2.B
|
3.A
|
4.A
|
5.C
|
6.A
|
7.B
|
8.A
|
9.C
|
10.D
|
|
11.D
|
12.B
|
13.B
|
14.B
|
15.C
|
16.A
|
17.C
|
18.D
|
19.B
|
20.C
|
|
21.A
|
22.D
|
23.A
|
24.B
|
25.A
|
26.B
|
27.C
|
28.B
|
29.D
|
30.D
|
Câu 1 (NB):
Phương pháp:
Mệnh đề là những khẳng định có tính đúng hoặc sai.
Cách giải:
Câu a) là câu cảm thán không phải là mệnh đề.
Các câu b, c, d là mệnh đề => Có 3 mệnh đề.
Chọn C.
Câu 2 (NB):
Phương pháp:
Cho số gần đúng a với độ chính xác d. Khi được yêu cầu làm tròn số a mà không nói rõ làm tròn đến hàng nào thì ta làm tròn số a đến hàng thấp nhất mà d nhỏ hơn 1 đơn vị của hàng đó.
Cách giải:
Vì độ chính xác đến hàng trăm (d = 123) nên ta làm tròn a đến hàng nghìn.
Vậy số quy tròn của a là 23748000.
Chọn B.
Câu 3 (TH):
Phương pháp:
Biến đổi \(\overrightarrow {MA} {\rm{ \;}} – \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\) về hai vectơ bằng nhau.
Xác định vị trí điểm M dựa vào điều kiện vừa tìm được.
Cách giải:
Ta có \(\overrightarrow {MA} {\rm{ \;}} – \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\)\( \Leftrightarrow \overrightarrow {BA} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0{\rm{ \;}} \Leftrightarrow \overrightarrow {MC} {\rm{ \;}} = \overrightarrow {AB} \)
\( \Rightarrow \) MABC là hình bình hành.
Chọn A.
Câu 4 (NB):
Phương pháp:
Sử dụng định lí cosin trong tam giác tại đỉnh C: \({c^2} = {a^2} + {b^2} – 2ab\cos C\).
Cách giải:
Ta có: \({c^2} = {a^2} + {b^2} – 2ab\cos C\).
\(\begin{array}{*{20}{l}}{ \Rightarrow A{B^2} = B{C^2} + A{C^2} – 2BC.AC.\cos C}\\{ \Rightarrow 5 = B{C^2} + 2 – 2.BC.\sqrt 2 .\frac{{\sqrt 2 }}{2}}\\{ \Leftrightarrow B{C^2} – 2BC – 3 = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{BC = 3{\mkern 1mu} {\mkern 1mu} \left( {tm} \right)}\\{BC = {\rm{ \;}} – 1{\mkern 1mu} {\mkern 1mu} \left( {ktm} \right)}\end{array}} \right.}\end{array}\)
Vậy BC = 3.
Chọn A.
Câu 5 (NB):
Phương pháp:
Cặp số nào thỏa mãn bất phương trình là nghiệm của bất phương trình.
Cách giải:
Thay cặp số (x;y) = (0;4) vào bất phương trình: 0 – 2.4 + 5 > 0 => Sai.
Thay cặp số (x;y) = (2;5) vào bất phương trình: 2 – 2. 5 + 5 > 0 => Sai.
Thay cặp số (x;y) = (2;3) vào bất phương trình: 2 – 2.3 + 5 > 0 => Đúng.
Thay cặp số (x;y) = (1;4) vào bất phương trình: 1 – 2.4 + 5 > 0 => Sai.
Chọn C.
Câu 6 (TH):
Phương pháp:
Biến đổi \(\overrightarrow {MA} {\rm{ \;}} – \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\) về hai vectơ bằng nhau.
Xác định vị trí điểm M dựa vào điều kiện vừa tìm được.
Cách giải:
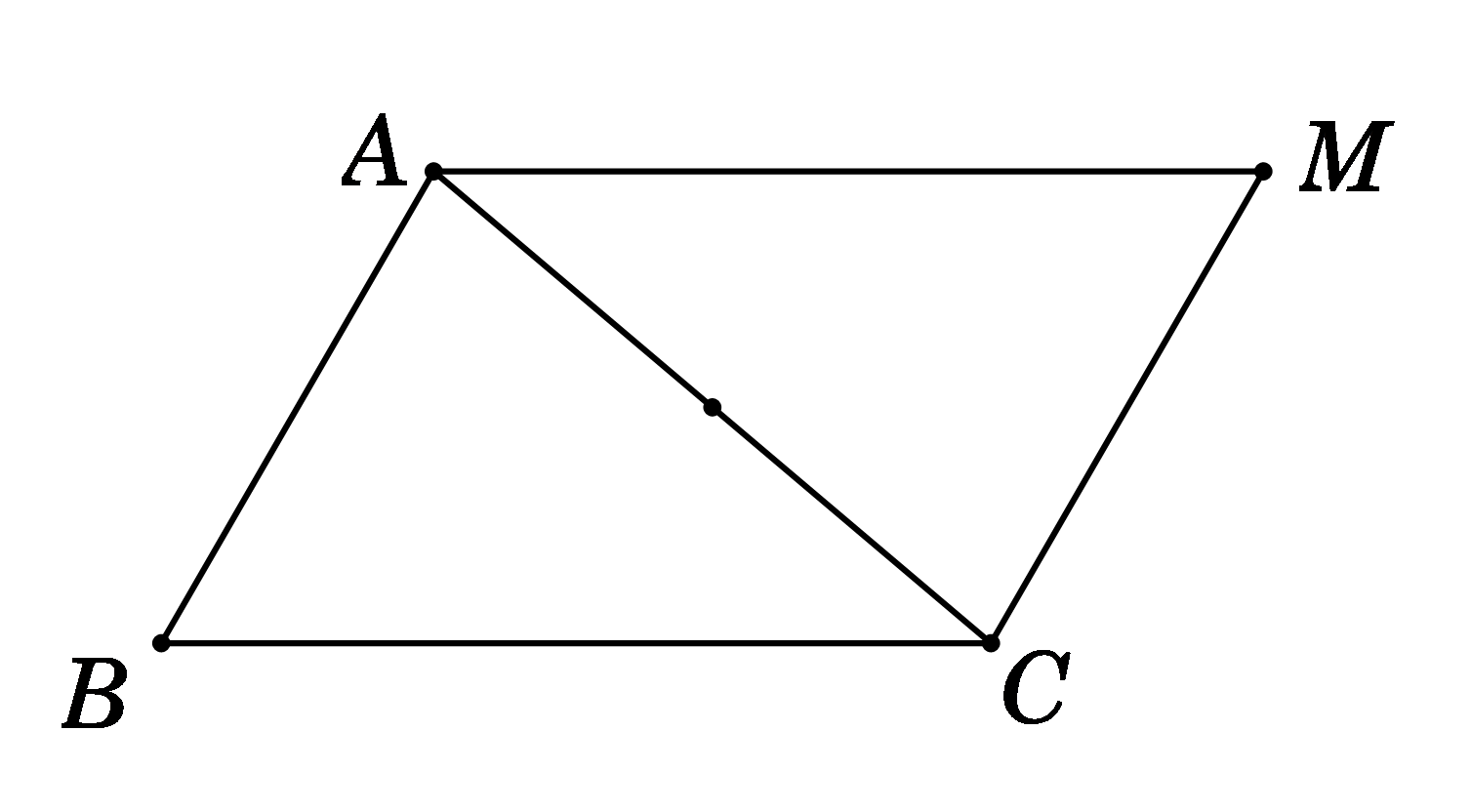
Ta có \(\overrightarrow {MA} {\rm{ \;}} – \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\)\( \Leftrightarrow \overrightarrow {BA} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0{\rm{ \;}} \Leftrightarrow \overrightarrow {MC} {\rm{ \;}} = \overrightarrow {AB} \)
\( \Rightarrow \) MABC là hình bình hành.
Chọn A.
Câu 7 (NB):
Phương pháp:
Tính \(\angle C = {180^0} – \left( {\angle A + \angle B} \right)\).
Sử dụng định lí sin: \(\frac{c}{{\sin C}} = 2R\).
Cách giải:
Ta có: \(\angle C = {180^0} – \left( {\angle A + \angle B} \right) = {60^0}\).
Áp dụng định lí sin ta có: \(\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{6}{{2\sin {{60}^0}}} = 2\sqrt 3 \).
Chọn B.
Câu 8 (VD):
Phương pháp:
Sử dụng hệ quả định lí cosin.
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{\frac{{\cos A}}{a} + \frac{{\cos B}}{b} + \frac{{\cos C}}{c}}\\{ = \frac{{{b^2} + {c^2} – {a^2}}}{{2bca}} + \frac{{{a^2} + {c^2} – {b^2}}}{{2acb}} + \frac{{{a^2} + {b^2} – {c^2}}}{{2abc}}}\\{ = \frac{{{b^2} + {c^2} – {a^2} + {a^2} + {c^2} – {b^2} + {a^2} + {b^2} – {c^2}}}{{2abc}}}\\{ = \frac{{{a^2} + {b^2} + {c^2}}}{{2abc}}}\end{array}\)
Chọn A.
Câu 9 (TH):
Phương pháp:
Giải phương trình, bất phương trình.
Xác định tập hợp \(A\), \(B\) bằng phương pháp liệt kê phần tử, đưa về cách viết khoảng, nửa khoảng.
Xác định \(A \cap B\); \(A \cup B\); \(A\backslash B\); \(B\backslash A\).
Cách giải:
*) \({x^2} – 7x + 6 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x – 1 = 0}\\{x – 6 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 6}\end{array}} \right.\) (thỏa mãn)
\( \Rightarrow A = \left\{ {1;{\mkern 1mu} {\mkern 1mu} 6} \right\}\)
*) \(\left| x \right| > 4 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x < {\rm{\;}} – 4}\\{x > 4}\end{array}} \right.\)\( \Rightarrow x \in \left( { – \infty ;{\mkern 1mu} – 4} \right) \cup \left( {4;{\mkern 1mu} + \infty } \right)\)
\( \Rightarrow B = \left( { – \infty ;{\mkern 1mu} – 4} \right) \cup \left( {4;{\mkern 1mu} + \infty } \right)\)
Ta có:
\(A \cup B = \left( { – \infty ;{\mkern 1mu} – 4} \right) \cup \left\{ 1 \right\} \cup \left( {4;{\mkern 1mu} + \infty } \right)\) , \(A \cap B = \left\{ 6 \right\}\)
\(B\backslash A = \left( { – \infty ;{\mkern 1mu} – 4} \right) \cup \left( {4;{\mkern 1mu} {\mkern 1mu} 6} \right) \cup \left( {6; + \infty } \right)\), \(A\backslash B = \left\{ 1 \right\}\)
Vậy đáp án đúng là: \(\left( {A\backslash B} \right) \subset A\)
Chọn C.
Câu 10 (TH):
Phương pháp:
Sử dụng khái niệm các phép toán trên tập hợp.
Cách giải:
Dễ thấy phần tô màu không thuộc A nên loại đáp án A, B.
Phần tô màu trong hình vẽ biểu diễn cho tập hợp \(\left( {B \cap C} \right)\backslash A.\)
Chọn D.
Câu 11 (TH):
Phương pháp:
Tính PR và QR theo h = AR và \(\tan \alpha {\rm{ \;}} = \tan {65^0},{\mkern 1mu} {\mkern 1mu} \tan \beta {\rm{ \;}} = \tan {79^0}\).
Sử dụng d = PQ = PR – QR, tính d.
Tính chiều cao tòa nhà bằng d + RO.
Cách giải:
Đặt d = PQ = LM = 50m, h = AR là chiều cao từ giác kế đến đỉnh tòa nhà.
Ta có: \(\angle APR = \alpha {\rm{ \;}} = {65^0},{\mkern 1mu} {\mkern 1mu} \angle AQR = \beta {\rm{ \;}} = {79^0}\).
Gọi \({d_1} = PR = \frac{h}{{\tan \alpha }},{\mkern 1mu} {\mkern 1mu} {d_2} = QR = \frac{h}{{\tan \beta }}\), ta có:
\(\begin{array}{*{20}{l}}{d = {d_1} – {d_2} = \frac{h}{{\tan \alpha }} – \frac{h}{{\tan \beta }} = h\left( {\frac{1}{{\tan \alpha }} – \frac{1}{{\tan \beta }}} \right)}\\{ \Rightarrow h = \frac{d}{{\frac{1}{{\tan \alpha }} – \frac{1}{{\tan \beta }}}} = \frac{{50}}{{\frac{1}{{\tan {{65}^0}}} – \frac{1}{{\tan {{79}^0}}}}} \approx 183,9{\mkern 1mu} {\mkern 1mu} \left( m \right)}\end{array}\)
Vậy chiều cao của tòa nhà là AR + RO \( \approx 183,9 + 1,4 = 185,3{\mkern 1mu} {\mkern 1mu} \left( m \right)\).
Chọn D.
Câu 12 (TH):
Phương pháp:
Dùng công thức \({\sin ^2}x + {\cos ^2}x = 1\) để tính cos x
Cách giải:
\(\begin{array}{*{20}{l}}{\sin x = \frac{1}{{\sqrt 3 }} \Rightarrow \sin {x^2} = \frac{1}{3} \Rightarrow {{\cos }^2}x = 1 – {{\sin }^2}x = 1 – \frac{1}{3} = \frac{2}{3}}\\{ \Rightarrow 2{{\sin }^2}x – {{\cos }^2}x = 2.\frac{1}{3} – \frac{2}{3} = 0}\end{array}\)
Chọn B.
Câu 13 (TH):
Phương pháp:
+) Giải phương trình, bất phương trình.
+) Tìm giao của hai tập hợp tức là xác định các phần tử chung của hai tập hợp đó.
Cách giải:
*) Xét tập hợp \(A = \left\{ {x \in \mathbb{R}|\left( {2{x^2} – 7x + 5} \right)\left( {x – 2} \right) = 0} \right\}\).
Ta có: \(\left( {2{x^2} – 7x + 5} \right)\left( {x – 2} \right) = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2{x^2} – 7x + 5 = 0}\\{x – 2 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{5}{2}}\\{x = 1}\\{x = 2}\end{array}} \right.\) (thỏa mãn)
\( \Rightarrow A = \left\{ {1;{\mkern 1mu} {\mkern 1mu} 2;{\mkern 1mu} {\mkern 1mu} \frac{5}{2}} \right\}\).
*) Xét tâp hợp \(B = \left\{ {x \in \mathbb{Z}| – 3 < 2x + 1 < 5} \right\}\).
Ta có: \( – 3 < 2x + 1 < 5 \Leftrightarrow {\rm{\;}} – 4 < 2x < 4 \Leftrightarrow {\rm{\;}} – 2 < x < 2\)
Mà \(x \in \mathbb{Z} \Rightarrow x \in \left\{ { – 1;{\mkern 1mu} {\mkern 1mu} 0;{\mkern 1mu} {\mkern 1mu} 1} \right\}\).
\( \Rightarrow B = \left\{ { – 1;{\mkern 1mu} {\mkern 1mu} 0;{\mkern 1mu} {\mkern 1mu} 1} \right\}\).
Vậy \(A \cap B = \left\{ 1 \right\}\).
Chọn B.
Câu 14 (TH):
Phương pháp:
Tìm \({\sin ^2}\alpha \) dựa vào đẳng thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
Chia cả tử và mẫu của P cho \(\sin \alpha \), tính P theo \(\cos \alpha \) và \({\sin ^2}\alpha \).
Cách giải:
Chia cả tử và mẫu cho \(\sin \alpha {\rm{ \;}} \ne 0\) ta được:
\(\begin{array}{*{20}{l}}{P = \frac{{\tan \alpha {\rm{ \;}} + 2\cot \alpha }}{{2\tan \alpha {\rm{ \;}} + 3\cot \alpha }}}\\{P = \frac{{\frac{1}{{\cos \alpha }} + \frac{{2\cos \alpha }}{{{{\sin }^2}\alpha }}}}{{\frac{2}{{\cos \alpha }} + \frac{{3\cos \alpha }}{{{{\sin }^2}\alpha }}}}}\end{array}\)
Ta có:
\(\begin{array}{*{20}{l}}{{{\sin }^2}\alpha {\rm{ \;}} + {{\cos }^2}\alpha {\rm{ \;}} = 1}\\{ \Rightarrow {{\sin }^2}\alpha {\rm{ \;}} + {{\left( {\frac{1}{4}} \right)}^2} = 1}\\{ \Leftrightarrow {{\sin }^2}\alpha {\rm{ \;}} = \frac{{15}}{{16}}}\end{array}\)
Khi đó: \(P = \frac{{\frac{1}{{\frac{1}{4}}} + \frac{{2.\frac{1}{4}}}{{\frac{{15}}{{16}}}}}}{{\frac{2}{{\frac{1}{4}}} + \frac{{3.\frac{1}{4}}}{{\frac{{15}}{{16}}}}}} = \frac{{\frac{{68}}{{15}}}}{{\frac{{44}}{5}}} = \frac{{17}}{{33}}\).
Chọn B.
Câu 15 (TH):
Phương pháp:
Vì vật đứng yên nên \(\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} {\rm{ \;}} + \overrightarrow {{F_3}} {\rm{ \;}} = \vec 0\).
Xác định \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} } \right|\), dựa vào tam giác MAB đều.
Cách giải:
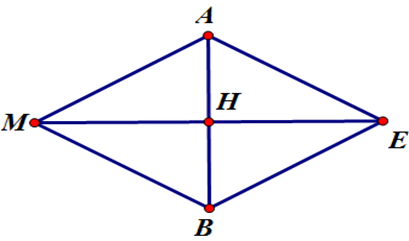
Ta có tam giác MAB đều.
Do vật đứng yên nên ta có: \(\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} {\rm{ \;}} + \overrightarrow {{F_3}} {\rm{ \;}} = \vec 0\)\( \Rightarrow \overrightarrow {{F_3}} {\rm{ \;}} = {\rm{ \;}} – (\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} )\)\( \Rightarrow \left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} } \right|\)
\( \Rightarrow \left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {ME} } \right| = 2MH = 2.50\frac{{\sqrt 3 }}{2} = 50\sqrt 3 \)
(với MAEB là hình bình hành tâm \(H\)).
Chọn C.
Câu 16 (TH):
Phương pháp:
Đặt \(\overrightarrow {AB} {\rm{ \;}} = \vec u\), \(\overrightarrow {BC} {\rm{ \;}} = \vec v\) suy ra \(\vec u + \vec v = \overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} = \overrightarrow {AC} \).
Xét các trường hợp A, B, C thẳng hàng; A, B, C không thẳng hàng.
Ngoài ra, có thể chỉ ra các đáp án sai bằng cách chỉ ra một trường hợp mà mệnh đề đó không đúng.
Cách giải:
Đặt \(\overrightarrow {AB} {\rm{ \;}} = \vec u\), \(\overrightarrow {BC} {\rm{ \;}} = \vec v\) khi đó ta có \(\vec u + \vec v = \overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} = \overrightarrow {AC} \)
Nếu A,B,C thẳng hàng và \(B\) nằm giữa A,C thì \(\left| {\vec u + \vec v} \right| = \left| {\vec u} \right| + \left| {\vec v} \right|\)
Nếu A,B,C thẳng hàng và \(B\)không nằm giữa A,C thì \(\left| {\vec u + \vec v} \right| < \left| {\vec u} \right| + \left| {\vec v} \right|\)
Nếu A,B,C không thẳng hàng thì trong tam giác ABC có \(AB + BC > AC\). Suy ra \(\left| {\vec u + \vec v} \right| < \left| {\vec u} \right| + \left| {\vec v} \right|\)
Do đó \(\left| {\vec u + \vec v} \right| \le \left| {\vec u} \right| + \left| {\vec v} \right|\)
Từ đó suy ra, đáp án B đúng
Đáp án A, C sai vì chọn \(\vec v = \vec 0\) thì có \(\left| {\vec u + \vec w} \right| \ge \left| {\vec u} \right| + \left| {\vec w} \right|\) (sai theo chứng minh ở trên).
Đáp án D sai vì chọn \(\vec u = \vec 0\) và \(\vec v \ne \vec 0\) thì có \(\left| {\vec v} \right| \le {\rm{ \;}} – \left| {\vec v} \right|\)\( \Rightarrow \) vô lý vì độ dài véctơ khác vectơ-không là một số dương.
Chọn A.
Câu 17 (VD):
Phương pháp:
Tính số trung bình cộng để so sánh tuổi thọ của từng loại bút.
Tính phương sai, độ lệch chuẩn để so sánh sự đồng đều về chất lượng của từng loại bút.
Cách giải:
*) Loại bút A:
Số trung bình: \(\overline {{x_{\rm{A}}}} {\rm{\;}} = \frac{{23 + 25 + 27 + 28 + 30 + 35}}{6} = 28\) (giờ)
Phương sai: \(s_A^2 = \frac{1}{6}\left[ {{{\left( {23 – 28} \right)}^2} + {{\left( {25 – 28} \right)}^2} + {{\left( {27 – 28} \right)}^2} + {{\left( {28 – 28} \right)}^2} + {{\left( {30 – 28} \right)}^2} + {{\left( {35 – 28} \right)}^2}} \right] \approx 14,7\) (giờ)
Độ lệch chuẩn: \({s_A} = \sqrt {s_A^2} {\rm{\;}} = \sqrt {14,7} {\rm{\;}} \approx 3,83\) (giờ)
*) Loại bút B:
Số trung bình: \(\overline {{x_B}} {\rm{\;}} = \frac{{16 + 22 + 28 + 33 + 46}}{5} = 29\) (giờ)
Phương sai: \(s_B^2 = \frac{1}{5}\left[ {{{\left( {16 – 29} \right)}^2} + {{\left( {22 – 29} \right)}^2} + {{\left( {28 – 29} \right)}^2} + {{\left( {33 – 29} \right)}^2} + {{\left( {46 – 29} \right)}^2}} \right] = 104,8\) (giờ)
Độ lệch chuẩn: \({s_B} = \sqrt {s_B^2} {\rm{\;}} = \sqrt {104,8} {\rm{\;}} \approx 10,24\) (giờ)
Vì \(\overline {{x_{\rm{A}}}} {\rm{\;}} < \overline {{x_B}} \) nên loại bút B có thời gian sử dụng lâu hơn.
Vì \(s_A^2 < s_B^2\) và \(s_A^{} < s_B^{}\) nên chất lượng của bút B không đồng đều.
Vậy loại bút B có thời gian sử dụng lâu hơn và chất lượng của loại bút B không đồng đều.
Chọn C.
Câu 18 (NB):
Phương pháp:
Áp dụng lý thuyết về phương sai và độ lệch chuẩn.
Cách giải:
Ta có: \(s = \sqrt {{s^2}} \) với \(s\) là độ lệch chuẩn và \({s^2}\) là phương sai của số liệu thống kê.
Chọn D.
Câu 19 (TH):
Phương pháp:
Sử dụng công thức: \(\overrightarrow {BA} .\overrightarrow {BC} {\rm{ \;}} = BA.BC.\cos \angle \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right).\)
Cách giải:
Vì ABC là tam giác vuông cân tại A nên \(BC = AB\sqrt 2 {\rm{ \;}} = 6\sqrt 2 \) và \(\left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = \angle ABC = {45^0}\).
Vậy \(\overrightarrow {BA} .\overrightarrow {BC} {\rm{ \;}} = BA.BC.\cos \angle \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right)\)
\( = 6.6\sqrt 2 .\cos {45^0} = 6.6\sqrt 2 .\frac{{\sqrt 2 }}{2} = 36.\)
Chọn B.
Câu 20 (TH):
Phương pháp:
– Mốt là giá trị có tần số lớn nhất trong bảng số liệu, kí hiệu là \({M_0}\)
– Xác định số trung vị:
Sắp xếp mẫu số liệu kích thước \(N\) theo thứ tự không giảm (tăng dần) hoặc không tăng (giảm dần):
+ Nếu \(N\) lẻ \( \Rightarrow {M_e} = \) số đứng thứ \(\frac{{N + 1}}{2}\) (chính giữa)
+ Nếu \(N\) chẵn \( \Rightarrow {M_e} = \) trung bình cộng hai số đứng giữa là \(\frac{N}{2}\) và \(\frac{N}{2} + 1\)
Cách giải:
Bảng phân bố tần số, sắp xếp theo thứ tự tăn dần về thời gian:

+) Vì \(x = 1\) có tần số lớn nhất \(n = 2\)\( \Rightarrow {M_0} = 1\) là Mốt của bảng số liệu trên.
+) Vì \(N = 9\) (lẻ) \( \Rightarrow \) Số trung vị \({M_e} = {x_{\frac{{N + 1}}{2}}} = {x_5} = 1,5\) (phút)
Chọn C.
Câu 21 (NB):
Phương pháp:
Xét điểm gốc tọa độ để xác định miền nghiệm của bất phương trình.
Cách giải:
Thay \(x = 0,y = 0\) vào BPT \(2x – 3y + 6 \ge 0\) ta được: \(2.0 – 3.0 + 6 \ge 0\) (đúng)
Nên O(0,0) thuộc miền nghiệm nên
Miền nghiệm nửa mặt phẳng có bờ là d chứa gốc tọa độ O và có lấy đường thẳng d
Chọn A.
Câu 22 (NB):
Phương pháp:
Vẽ đồ thị hoặc thử các đáp án
Cách giải:
Xét hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 2y > – 3\quad (1)}\\{3x – y < 5\quad (2)}\\{y – 1 > 0\quad (3)}\end{array}} \right.\).
\(\left( { – 2; – 1} \right)\) không thỏa mãn BPT (3)
\(\left( {2;0} \right)\) không thỏa mãn BPT (3)
\(\left( {3;2} \right)\) không thỏa mãn BPT (2)
\(\left( {0,2} \right)\)thỏa mãn cả 3 BPT nên là nghiệm của hệ.
Chọn D.
Câu 23 (TH):
Phương pháp:
Nhóm thích hợp, sử dụng mối quan hệ giá trị lượng giác của hai góc bù nhau: \(\cos \left( {{{180}^0} – \alpha } \right) = {\rm{ \;}} – \cos \alpha \).
Cách giải:
\(\begin{array}{*{20}{l}}{B = \cos {0^0} + \cos {{20}^0} + \cos {{40}^0} + … + \cos {{160}^0} + \cos {{180}^0}}\\{B = \left( {\cos {0^0} + \cos {{180}^0}} \right) + \left( {\cos {{20}^0} + \cos {{160}^0}} \right) + \left( {\cos {{40}^0} + \cos {{140}^0}} \right) + … + \left( {\cos {{80}^0} + \cos {{100}^0}} \right)}\\{B = \left( {\cos {0^0} – \cos {0^0}} \right) + \left( {\cos {{20}^0} – \cos {{20}^0}} \right) + \left( {\cos {{40}^0} – \cos {{40}^0}} \right) + … + \left( {\cos {{80}^0} – \cos {{80}^0}} \right)}\\{B = 0}\end{array}\)
Chọn A
Câu 24 (TH):
Phương pháp:
Sử dụng công thức \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = BM.BA.\cos \left( {\overrightarrow {BM} ,\overrightarrow {BA} } \right).\)
Cách giải:
Ta có: \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} – \frac{1}{3}\overrightarrow {BC} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} – \frac{1}{3}BC.BA.\cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right).\)
Vì tam giác ABC đều nên \(\cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right) = \angle ABC = {60^0}\).
\( \Rightarrow \overrightarrow {BM} .\overrightarrow {BA} = – \frac{1}{3}.6.6.\frac{{\sqrt 3 }}{2} = {\rm{ \;}} – 6\sqrt 3 .\)
Chọn B.
Câu 25 (NB):
Phương pháp:
Xác định số gần đúng a và độ chính xác d.
Tính số đúng \(\bar a = a \pm d \Rightarrow a – d \le \bar a \le a + d\).
Cách giải:
Gọi \(\bar a\) là độ dài đúng của dây cầu \( \Rightarrow \bar a = 996m \pm 0,5m\).
\(\begin{array}{*{20}{l}}{ \Rightarrow 996 – 0,5 \le \bar a \le 996 + 0,5}\\{ \Leftrightarrow 995,5 \le \bar a \le 996,5}\end{array}\)
Vậy độ dài đúng của cầu là một số nằm trong khoảng 995,5m đến 996,5m.
Chọn A.
Câu 26 (TH):
Phương pháp:
Tính diện tích hình chữ nhật bằng dài nhân rộng.
Sai số tương đối \({\delta _a} \le \frac{d}{{\left| a \right|}}\).
Cách giải:
Diện tích hình chữ nhật là:
\(\begin{array}{l}S = \left( {2m \pm 0,01m} \right)\left( {5m \pm 0,02m} \right)\\\,\,\,\, = \left( {2.5{m^2} \pm \left( {2.0,02 + 5.0,01 + 0,01.0,02} \right){m^2}} \right)\\\,\,\,\, = \left( {10{m^2} \pm 0,04001{m^2}} \right)\end{array}\)
\( \Rightarrow a = 10,\,\,d = 0,04001\).
\( \Rightarrow {\delta _a} \le \frac{d}{{\left| a \right|}} = \frac{{0,04001}}{{10}} = 0,004001 = 4,001\) ‰.
Chọn B.
Câu 27 (TH):
Phương pháp:
Khoảng biến thiên, kí hiệu là R, là hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất trong mẫu số liệu.
Cách giải:
Giá trị lớn nhất trong mẫu số liệu là 20.
Giá trị nhỏ nhất trong mẫu số liệu là 5.
Vậy khoảng biến thiên R = 20 – 5 = 15.
Chọn C.
Câu 28 (VD):
Phương pháp:
Sử dụng công thức \(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) – n\left( {A \cap B} \right)\).
Cách giải:
Gọi A là tập hợp các bạn đăng kí tiết mục múa \( \Rightarrow n\left( A \right) = 9.\)
B là tập hợp các bạn đăng kí tiết mục diễn kịch \( \Rightarrow n\left( B \right) = 13.\)
\( \Rightarrow A \cap B:\) tập hợp các bạn đăng kí cả 2 tiết mục múa và diễn kịch \( \Rightarrow n\left( {A \cap B} \right) = 4.\)
\(A \cup B\): tập hợp các bạn tham gia ít nhất 1 tiết mục.
Ta có: \(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) – n\left( {A \cap B} \right)\)
\( \Rightarrow \) Số học sinh lớp 10A tham gia văn nghệ là: \(n\left( {A \cup B} \right) = 9 + 13 – 4 = 18.\)
Chọn B.
Câu 29 (TH):
Phương pháp:
Gọi M là trung điểm BC.
Sử dụng tính chất trung điểm.
Cách giải:
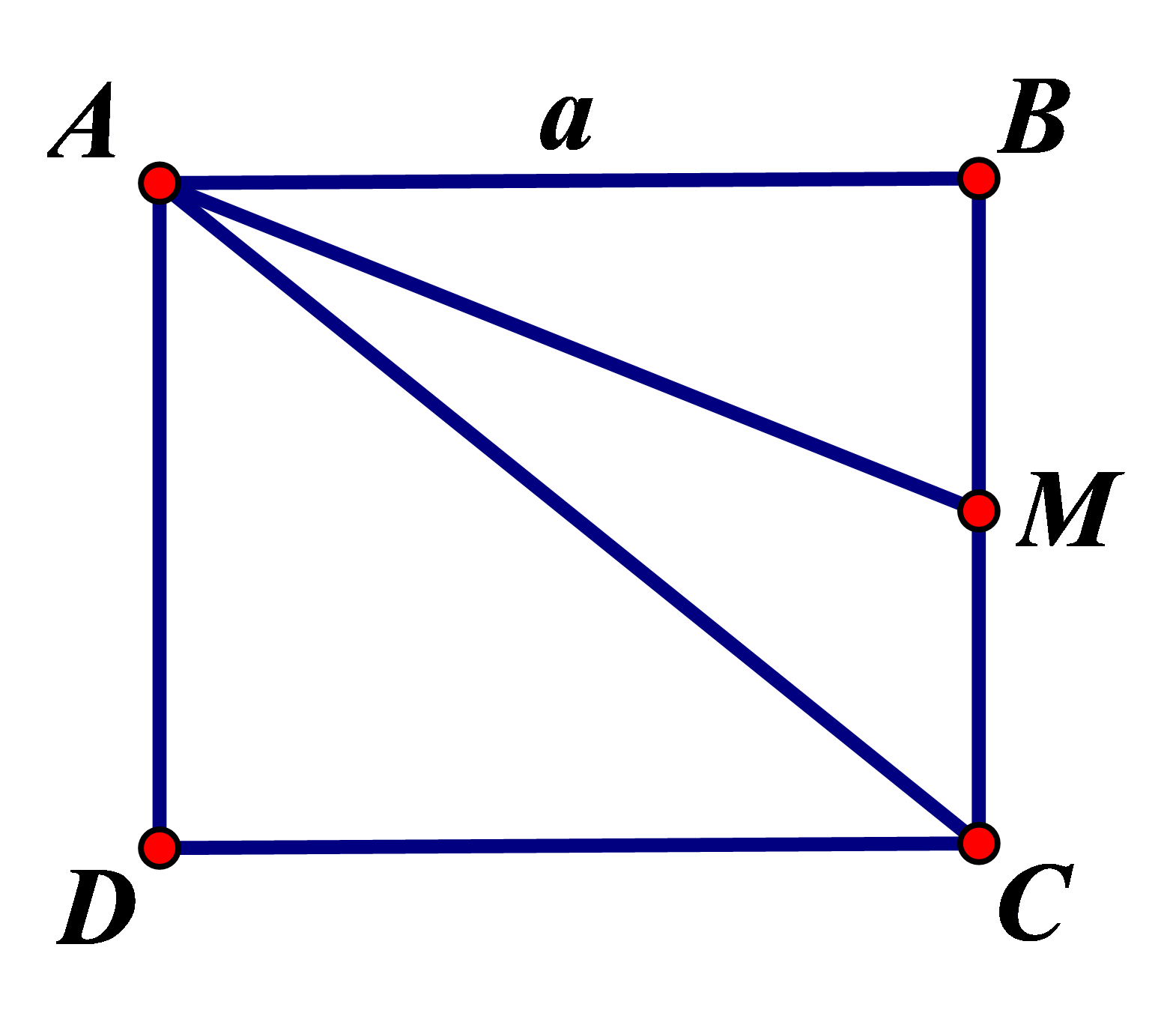
Gọi \(M\) là trung điểm BC.
Ta có: \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| = 2AM = 2\sqrt {A{B^2} + B{M^2}} {\rm{ \;}} = 2\sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} {\rm{ \;}} = a\sqrt 5 \).
Chọn D.
Câu 30 (TH):
Phương pháp:
Sử dụng định nghĩa tích vô hướng của hai vectơ: \(\vec a.\vec b{\rm{ \;}} = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\).
Cách giải:
Ta có:
\(\begin{array}{l}\vec a.\vec b = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\\ \Leftrightarrow 2\vec a.\vec b = 2\left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\\ \Leftrightarrow \left| {\vec a} \right|.\left| {\vec b} \right| = 2\left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\\ \Leftrightarrow \left| {\vec a} \right|.\left| {\vec b} \right|\left[ {2\cos \left( {\vec a,\vec b} \right) – 1} \right] = 0\\ \Leftrightarrow \cos \left( {\vec a,\vec b} \right) = \frac{1}{2}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} \vec a \ne \vec 0,{\mkern 1mu} {\mkern 1mu} \vec b \ne \vec 0} \right)\end{array}\)
\( \Leftrightarrow \left( {\vec a,\vec b} \right) = {60^0}.\)
Chọn D.
Phần 2: Tự luận (4 điểm)
Câu 1 (VD):
Phương pháp:
a) Sử dụng quy tắc hiệu, đưa về tính chất vectơ trọng tâm tam giác.
b) Sử dụng tính chất vectơ trung tuyến.
Cách giải:
a) Ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {KA} {\rm{ \;}} + 2\overrightarrow {KB} {\rm{ \;}} = \overrightarrow {CB} }\\{ \Leftrightarrow \overrightarrow {KA} {\rm{ \;}} + 2\overrightarrow {KB} {\rm{ \;}} = \overrightarrow {KB} {\rm{ \;}} – \overrightarrow {KC} }\\{ \Leftrightarrow \overrightarrow {KA} {\rm{ \;}} + \overrightarrow {KB} {\rm{ \;}} + \overrightarrow {KC} {\rm{ \;}} = \vec 0}\end{array}\)
Vậy K là trọng tâm tam giác ABC.
b) Gọi I là trung điểm của BC ta có:
\(\begin{array}{l}\overrightarrow {MA} + 2\overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {MA} + 2\left( {\overrightarrow {MB} + \overrightarrow {MC} } \right) = \overrightarrow 0 \\ \Leftrightarrow \left( {\overrightarrow {MI} + \overrightarrow {IA} } \right) + 4\overrightarrow {MI} = \overrightarrow 0 \\ \Leftrightarrow 5\overrightarrow {MI} + \overrightarrow {IA} = 0\\ \Leftrightarrow \overrightarrow {IM} = \frac{1}{5}\overrightarrow {IA} \end{array}\)
Vậy M là thuộc IA sao cho \(IM = \frac{1}{5}IA\).
Câu 2 (VD):
Phương pháp:
Tính giá trị trung bình \(\bar x\).
Phương sai \({s^2} = \frac{{{{\left( {{x_1} – \bar x} \right)}^2} + {{\left( {{x_2} – \bar x} \right)}^2} + … + {{\left( {{x_n} – \bar x} \right)}^2}}}{n}\).
Độ lệch chuẩn \(s = \sqrt {{s^2}} \).
Cách giải:
a) Mẫu số liệu:
23 25 26 27 27 27 27 21 19 18
b) Số trung bình cộng:
\(\bar x = \frac{{23 + 25 + 26 + 27 + 27 + 27 + 27 + 21 + 19 + 18}}{{10}} = 24\) (0C).
Phương sai:
\({s^2} = \frac{{{{\left( {23 – 24} \right)}^2} + {{\left( {25 – 24} \right)}^2} + 4.{{\left( {27 – 24} \right)}^2} + {{\left( {26 – 24} \right)}^2} + {{\left( {21 – 24} \right)}^2} + {{\left( {19 – 24} \right)}^2} + {{\left( {18 – 24} \right)}^2}}}{{10}} = 11,2\)
Độ lệch chuẩn:
\(s = \sqrt {{s^2}} {\rm{ \;}} = \sqrt {11,2} {\rm{ \;}} = \frac{{2\sqrt {70} }}{5} \approx 3,35\).
Câu 3 (VDC):
Phương pháp:
a) Áp dụng định lí cosin và định lí sin
b) Áp dụn định lí cosin và công thức \(\cos A = 1 – 2{\sin ^2}\frac{A}{2}\)
Cách giải:
a) Áp dụng định lí cosin và định lí sin ta có:
\(\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}};\sin A = \frac{a}{{2R}}\)
\( \Rightarrow \cot A = \frac{{\cos A}}{{\sin A}} = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}.\frac{{2R}}{a} = \frac{{{b^2} + {c^2} – {a^2}}}{{abc}}R\)
Tương tự ta cũng có: \(\cot B = \frac{{{a^2} + {c^2} – {b^2}}}{{abc}}R;\cot C = \frac{{{a^2} + {b^2} – {c^2}}}{{abc}}R\)
\(\begin{array}{l} \Rightarrow \cot A + \cot B + \cot C = \frac{{{b^2} + {c^2} – {a^2}}}{{abc}}R + \frac{{{a^2} + {c^2} – {b^2}}}{{abc}}R + \frac{{{a^2} + {b^2} – {c^2}}}{{abc}}R\\ = \frac{R}{{abc}}({b^2} + {c^2} – {a^2} + {a^2} + {c^2} – {b^2} + {a^2} + {b^2} – {c^2})\\ = \frac{R}{{abc}}({a^2} + {b^2} + {c^2}) = \frac{{{a^2} + {b^2} + {c^2}}}{{abc}}R\end{array}\)
b) Ta có: \(\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}\)
Mà \(\cos A = 1 – 2{\sin ^2}\frac{A}{2} \Rightarrow \sin \frac{A}{2} = \sqrt {\frac{{1 – \cos A}}{2}} \) (do \({0^ \circ } < \frac{A}{2} < {90^ \circ }\))
\(\begin{array}{l} \Rightarrow \sin \frac{A}{2} = \sqrt {\frac{{1 – \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}}}{2}} \\ \Leftrightarrow \sin \frac{A}{2} = \sqrt {\frac{{{a^2} – \left( {{b^2} + {c^2} – 2bc} \right)}}{{4bc}}} \\ \Leftrightarrow \sin \frac{A}{2} = \sqrt {\frac{{{a^2} – {{(b – c)}^2}}}{{4bc}}} \\ \Leftrightarrow \sin \frac{A}{2} = \sqrt {\frac{{(a – b + c)(a + b – c)}}{{4bc}}} \end{array}\)
Lại có: \(p = \frac{{a + b + c}}{2}\)\( \Rightarrow p – b = \frac{{a – b + c}}{2};p – c = \frac{{a + b – c}}{2}\)
\(\begin{array}{l} \Leftrightarrow \frac{{(a – b + c)(a + b – c)}}{4} = (p – b)(p – c)\\ \Leftrightarrow \sin \frac{A}{2} = \sqrt {\frac{{(p – b)(p – c)}}{{bc}}} \end{array}\)
Đề 5
I. Trắc nghiệm (7 điểm)
Câu 1: Mệnh đề nào sau đây sai?
A. Tam giác có hai góc bằng nhau thì góc thứ ba bằng nhau
B. Hai tam giác bằng nhau thì có diện tích bằng nhau
C. Tam giác có ba cạnh bằng nhau thì có ba góc bằng nhau
D. Hai tam giác có diện bằng nhau thì bằng nhau.
Câu 2: Cho mệnh đề P(x): “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 > 0\)”. Mệnh đề phủ định của mệnh đề P(x) là
A. “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 < 0\)”. B. “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 \le 0\)”.
C. “\(\exists x \in \mathbb{R}\), \({x^2} + x + 1 \le 0\)”. D. “\(\exists x \in \mathbb{R}\), \({x^2} + x + 1 > 0\)”.
Câu 3: Cho tập hợp \(A = \left\{ {x \in \mathbb{Z}|\frac{{{x^2} + 2}}{x} \in \mathbb{Z}} \right\}\). Hãy xác định tập \(A\) bằng cách liệt kê các phần tử.
A. \(A = \left\{ { – 2;;0;1;2} \right\}\) B. \(A = \left\{ { – 2; – 1;0;2} \right\}\) C. \(A = \left\{ { – 2; – 1;1;2} \right\}\) D. \(A = \left\{ { – 2; – 1;0;1;2} \right\}\)
Câu 4: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng:
A. \(A = \left\{ {x \in \mathbb{R}|\left| x \right| < 1} \right\}\) B. \(A = \left\{ {x \in \mathbb{Z}|6{x^2} – 7x + 1 = 0} \right\}\) C. \(A = \left\{ {x \in \mathbb{Z}|{x^2} – 4x + 2 = 0} \right\}\) D. \(A = \left\{ {x \in \mathbb{N}|{x^2} – 4x + 3 = 0} \right\}\)
Câu 5: Cho hai tập hợp \(A = \left( { – \infty ;2} \right]\) và \(B = \left( { – 3;5} \right]\). Tìm mệnh đề sai.
A. \(A \cap B = \left( { – 3;2} \right].\) B. \(A\backslash B = \left( { – \infty ; – 3} \right)\). C. \(A \cup B = \left( { – \infty ;5} \right]\). D. \(B\backslash A = \left( {2;5} \right]\).
Câu 6: Cho tập hợp: \(B = \left\{ {x;{\mkern 1mu} {\mkern 1mu} y;{\mkern 1mu} {\mkern 1mu} z;{\mkern 1mu} {\mkern 1mu} 1;{\mkern 1mu} {\mkern 1mu} 5} \right\}.\) Số tập hợp con của tập hợp \(B\) là
A. 29 B. 30 C. 31 D. 32
Câu 7: Mệnh đề “\(\exists x \in \mathbb{R},\,\,{x^2} = 2\)” khẳng định rằng:
A. Bình phương của mỗi số thực bằng 2.
B. Có ít nhất một số thực mà bình phương của nó bằng 2.
C. Chỉ có một số thực mà bình phương của nó bằng 2.
D. Nếu x là một số thực thì \({x^2} = 2\).
Câu 8: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. \(2{x^2} + 3y > 0\) B. \({x^2} + {y^2} < 2\) C. \(x + {y^2} \ge 0\) D. \(x + y \ge 0\)
Câu 9: Miền nghiệm của bất phương trình \(\left( {1 + \sqrt 3 } \right)x – \left( {1 – \sqrt 3 } \right)y \ge 2\) chứa điểm nào sau đây?
A. A(1;-1) B. B(-1;-1) C. C(-1;1) D. \(D\left( { – \sqrt 3 ;\sqrt 3 } \right)\)
Câu 10: (ID: 590544) Trong tam giác EFG, chọn mệnh đề đúng.
A. \(E{F^2} = E{G^2} + F{G^2} + 2EG.FG.\cos G.\) B. \(E{F^2} = E{G^2} + F{G^2} + 2EG.FG.\cos E.\)
C. \(E{F^2} = E{G^2} + F{G^2} – 2EG.FG.\cos E.\) D. \(E{F^2} = E{G^2} + F{G^2} – 2EG.FG.\cos G.\)
Câu 11: (ID: 590545) Cho tam giác ABC biết \(\frac{{\sin B}}{{\sin C}} = \sqrt 3 \) và \(AB = 2\sqrt 2 \). Tính AC.
A. \(2\sqrt 3 .\) B. \(2\sqrt 5 .\) C. \(2\sqrt 2 .\) D. \[2\sqrt 6 .\]
Câu 12: (ID: 590546) Cho tam giác ABC có b = 7, c = 5, \(\cos A = \frac{3}{5}.\) Độ dài đường cao \({h_a}\) của tam giác ABC là:
A. \(8.\) B. \(8\sqrt 3 .\) C. \(\frac{{7\sqrt 2 }}{2}.\) D. \(7\sqrt 2 .\)
Câu 13: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?
A. Nếu số nguyên n có tổng các chữ số bằng 9 thì số tự nhiên n chia hết cho 3.
B. Nếu x > y thì \({x^2} > {y^2}\).
C. Nếu x = y thì t.x = t.y.
D. Nếu x > y thì \({x^3} > {y^3}\).
Câu 14: Cho hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x – 5y – 1 > 0}\\{2x + y + 5 > 0}\\{x + y + 1 < 0}\end{array}} \right.\). Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
A. \(O\left( {0;0} \right)\) B. \(M\left( {1;0} \right)\) C. \(N\left( {0; – 2} \right)\) D. \(P\left( {0;2} \right)\)
Câu 15: Giá trị của biểu thức \(B = 4{a^2}{\sin ^2}{45^0} – 3{\left( {a\tan {{45}^0}} \right)^2} + {\left( {2a\cos {{45}^0}} \right)^2}\) với \(a = 1\) là:
A. 3. B. \( – \frac{1}{2}\). C. \(\frac{1}{2}\) D. 1.
Câu 16: Tính bán kính r của đường tròn nội tiếp tam giác đều cạnh a.
A. \(r = \frac{{a\sqrt 3 }}{4}\) B. \(r = \frac{{a\sqrt 2 }}{5}\) C. \(r = \frac{{a\sqrt 3 }}{6}\) D. \(r = \frac{{a\sqrt 5 }}{7}\)
Câu 17: Tam giác ABC có \(AB = \sqrt 2 ,\,\,AC = \sqrt 3 \) và \(C = {45^0}\). Tính độ dài cạnh BC.
A. \(BC = \sqrt 5 \) B. \(BC = \frac{{\sqrt 6 + \sqrt 2 }}{2}\) C. \(BC = \frac{{\sqrt 6 – \sqrt 2 }}{2}\) D. \(BC = \sqrt 6 \)
Câu 18: Cho ba mệnh đề sau, với \(n\) là số tự nhiên
(1) \(n + 8\) là số chính phương (2) Chữ số tận cùng của \(n\) là 4 (3) \(n – 1\) là số chính phương
Biết rằng có hai mệnh đề đúng và một mệnh đề sai, ngoài ra số chính phương chỉ có thể tận cùng là \[0,{\rm{ }}1,{\rm{ }}4,{\rm{ }}5,{\rm{ }}6,{\rm{ }}9\]. Hãy xác định mệnh đề nào, đúng mệnh đề nào sai?
A. Mệnh đề (2) và (3) là đúng, còn mệnh đề (1) là sai.
B. Mệnh đề (1) và (2) là đúng, còn mệnh đề (3) là sai.
C. Mệnh đề (1) là đúng, còn mệnh đề (2) và (3) là sai.
D. Mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai.
Câu 19: Phần không bị gạch trên hình vẽ dưới đây minh họa cho tập hợp nào?

A. \(\left( { – 3; + \infty } \right).\) B. \(\left( {5; + \infty } \right).\) C. \(\{ – 3;5\} \) D. \(\left( { – 3;5} \right].\)
Câu 20: Chọn khẳng định sai trong các khẳng định sau:
A. \(\sin (\pi + \alpha ) = \sin \alpha .\) B. \[\cos ( – \alpha ) = \cos \alpha .\] C. \(\tan (\pi – \alpha ) = – \tan \alpha \) D. \(\cot \left( {\frac{\pi }{2} – \alpha } \right) = \tan \alpha \)
Câu 21: Cho hai tập hợp \(A = ( – 1;4]\) và \(B = [ – 2; + \infty )\). Xác định tập hợp \({C_B}A\).
A. \({C_B}A = [ – 2; – 1] \cup (4; + \infty )\) B. \({C_B}A = (4; + \infty )\)
C. \({C_B}A = [ – 2; – 1) \cup [4; + \infty )\) D. \({C_B}A = [ – 2; – 1) \cup (4; + \infty )\)
Câu 22: Cho tam giác cân \[ABC\] có\(\widehat A = {120^0}\)và \[AB = AC = a\]. Lấy điểm \[M\]trên cạnh \[BC\] sao cho \(BM = \frac{{2BC}}{5}\). Tính độ dài \[AM.\]
A. \(\frac{{a\sqrt 3 }}{3}\) B. \(\frac{{11a}}{5}\) C. \(\frac{{a\sqrt 7 }}{5}\) D. \(\frac{{a\sqrt 6 }}{4}\)
Câu 23: Nửa mặt phẳng không bị gạch chéo ở hình dưới đây là miền nghiệm của bất phương trình nào trong các bất phương trình sau?
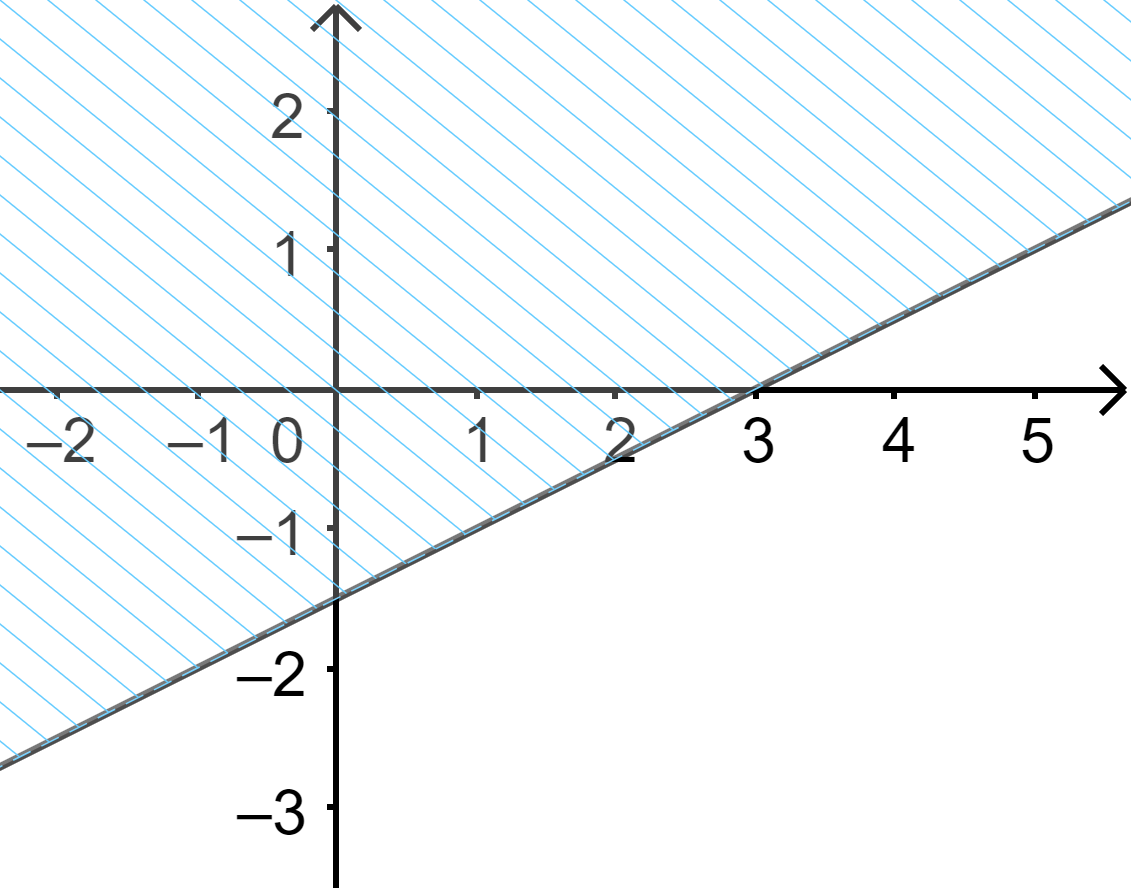
A. \(2x – y < 3\) B. \(2x – y > 3\) C. \(x – 2y < 3\) D. \(x – 2y > 3\)
Câu 24: Cho góc \(\alpha \) với \({0^0} < \alpha < {180^0}\). Tính giá trị của \(\cos \alpha \), biết \(\tan \alpha = – 2\sqrt 2 \).
A. \( – \frac{1}{3}.\) B. \(\frac{1}{3}.\) C. \(\frac{{2\sqrt 2 }}{3}.\) D. \(\frac{{\sqrt 2 }}{3}.\)
Câu 25: Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn cùng một điểm trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C. Ta đo được khoảng cách AB = 40cm, \(\angle CAB = {45^0}\), \(\angle CBA = {70^0}\). Vậy sau khi đo đạc và tính toán được khoảng cách AC gần nhất với giá trị nào sau đây?
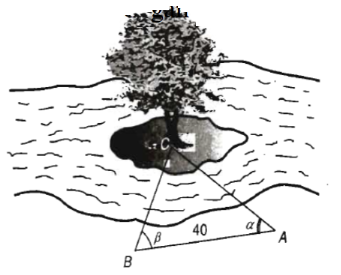
A. 53 m B. 30 m C. 41,5 m D. 41 m
Câu 26: Trái đất quay một vòng quanh mặt trời là 365 ngày. Kết quả này có độ chính xác là \(\frac{1}{4}\) ngày. Sai số tương đối là:
A. 0,0068%. B. 0,068%. C. 0,68%. D. 6,8%.
Câu 27: Cho mẫu số liệu: 1 3 6 8 9 12. Tứ phân vị của mẫu số liệu trên là:
A. Q1 = 3, Q2 = 6,5, Q3 = 9. B. Q1 = 1, Q2 = 6,5, Q3 = 12.
C. Q1 = 6, Q2 = 7, Q3 = 8. D. Q1 = 3, Q2 = 7, Q3 = 9.
Câu 28: Cho bốn điểm A,B,C,D phân biệt. Khi đó, \(\overrightarrow {AB} {\rm{ \;}} – \overrightarrow {DC} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} – \overrightarrow {AD} \) bằng véctơ nào sau đây?
A. \(\vec 0\) B. \(\overrightarrow {BD} \) C. \(\overrightarrow {AC} \) D. \(2\overrightarrow {DC} \)
Câu 29: Cho hình chữ nhật ABCD. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AC} {\rm{ \;}} = \overrightarrow {BD} \) B. \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} {\rm{ \;}} + \overrightarrow {AD} {\rm{ \;}} = \vec 0\)
C. \(\left| {\overrightarrow {AB} {\rm{ \;}} – \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AD} } \right|\) D. \(\left| {\overrightarrow {BC} {\rm{ \;}} + \overrightarrow {BD} } \right| = \left| {\overrightarrow {AC} {\rm{ \;}} – \overrightarrow {AB} } \right|\)
Câu 30: Cho ba lực \(\overrightarrow {{F_1}} {\rm{\;}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} {\rm{\;}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} {\rm{\;}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ lực \(\overrightarrow {{F_1}} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {{F_2}} \) đều bằng 50 N và tam giác MAB vuông tại M. Tìm cường độ lực \(\overrightarrow {{F_3}} \)
A. 86,60 N B. 100 N C. 70,71 N D. 70,17 N
Câu 31: Sản lượng lúa của 40 thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng tần số sau đây: (đơn vị: tạ)

Phương sai là
A. 1,24 B. 1,54 C. 22,1 D. 4,70
Câu 32: Cho tam giác ABC có trung tuyến BM và trọng tâm \(G\). Đặt \(\overrightarrow {BC} {\rm{\;}} = \vec a,{\mkern 1mu} {\mkern 1mu} \overrightarrow {BA} {\rm{\;}} = b\). Hãy phân tích vectơ \(\overrightarrow {BG} \) theo \(\vec a\) và \(\vec b\).
A. \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\) B. \(\overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\vec a + \frac{2}{3}\vec b\) C. \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{2}{3}\vec b\) D. \(\overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\vec a + \frac{1}{3}\vec b\)
Câu 33: Cho hình vuông ABCD cạnh \(a\), \(M\) là điểm thay đổi. Độ dài véctơ \(\vec u = \overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} {\rm{\;}} + \overrightarrow {MC} {\rm{\;}} – 3\overrightarrow {MD} \) là:
A. \(4a\sqrt 2 \) B. \(a\sqrt 2 \) C. \(3a\sqrt 2 \) D. \(2a\sqrt 2 \)
Câu 34: Cho tam giác ABC đều cạnh a, G là trọng tâm. Mệnh đề nào sau đây sai?
A. \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{1}{2}{a^2}.\) B. \(\overrightarrow {AC} .\overrightarrow {CB} = – \frac{1}{2}{a^2}.\) C. \(\overrightarrow {GA} .\overrightarrow {GB} = \frac{1}{6}{a^2}.\) D. \(\overrightarrow {AB} .\overrightarrow {AG} = \frac{1}{2}{a^2}.\)
Câu 35: Cho hình chữ nhật ABCD có \(AB = a\) và \(AD = a\sqrt 2 \). Gọi K là trung điểm của cạnh AD. Tính \(\overrightarrow {BK} .\overrightarrow {AC} \)
A. \(\overrightarrow {BK} .\overrightarrow {AC} = \overrightarrow 0 \) B. \(\overrightarrow {BK} .\overrightarrow {AC} = – {a^2}\sqrt 2 \) C. \(\overrightarrow {BK} .\overrightarrow {AC} = {a^2}\sqrt 2 \) D. \(\overrightarrow {BK} .\overrightarrow {AC} = 2{a^2}\)
II. Tự luận (3 điểm)
Câu 1: Cho hai tập hợp \(A = \left[ { – 2;{\mkern 1mu} {\mkern 1mu} 3} \right)\) và \(B = \left[ {1;6} \right)\). Xác định các tập hợp \(A \cup B,A \cap B,A{\rm{\backslash }}B,B{\rm{\backslash }}A\)
Câu 2: Bảo Anh và Quang ghi lại số tin nhắn điện thoại mà mỗi người nhận được từ ngày 1/11 đến ngày 15/11 ở bảng sau:

a) Hãy tìm phương sai của từng dãy số liệu.
b) Xác định các giá trị ngoại lệ (nếu có).
Câu 3: Cho tam giác ABC.
a) Xác định điểm I sao cho \(\overrightarrow {IA} + 3\overrightarrow {IB} – 2\overrightarrow {IC} = \overrightarrow 0 \)
b) Xác định điểm D sao cho \(3\overrightarrow {DB} – 2\overrightarrow {DC} = \overrightarrow 0 \)
c) Chứng minh ba điểm A, I, D thẳng hàng.
—–HẾT—–
Giải đề 5
HƯỚNG DẪN GIẢI CHI TIẾT
I. Trắc nghiệm (7 điểm)
|
1. B
|
2. C
|
3. C
|
4. C
|
5. B
|
6. D
|
7. B
|
|
8. D
|
9. A
|
10. D
|
11. D
|
12. C
|
13. D
|
14. C
|
|
15. D
|
16. C
|
17. B
|
18. D
|
19. D
|
20. A
|
21. A
|
|
22. C
|
23. D
|
24. C
|
25. C
|
26. A
|
27. D
|
28. A
|
|
29.A
|
30. C
|
31. B
|
32. A
|
33. D
|
34. C
|
35. A
|
Câu 1 (NB):
Phương pháp:
Mệnh đề là câu khẳng định, có tính đúng hoặc sai.
Cách giải:
(1) và (4) là mệnh đề.
Chọn B.
Câu 2 (TH):
Phương pháp:
Phủ định của mệnh đề “\(\forall x \in K,\,\,P\left( x \right)\)” là mệnh đề “\(\exists x \in K,\,\,\overline {P\left( x \right)} \)”.
Cách giải:
Mệnh đề phủ định của mệnh đề P(x): “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 > 0\)” là “\(\exists x \in \mathbb{R}\), \({x^2} + x + 1 \le 0\)”.
Chọn C.
Câu 3 (TH):
Phương pháp:
Giải nghĩa và giải tập hợp.
Cách giải:
Ta có \(\frac{{{x^2} + 2}}{x} = x + \frac{2}{x} \in \mathbb{Z}\) với \(x \in \mathbb{Z} \Leftrightarrow \frac{2}{x} \in \mathbb{Z} \Leftrightarrow 2{\mkern 1mu} {\mkern 1mu} \vdots {\mkern 1mu} {\mkern 1mu} x \Leftrightarrow x \in U\left( 2 \right) \Leftrightarrow x \in \left\{ { – 2; – 1;{\mkern 1mu} {\mkern 1mu} 1;{\mkern 1mu} {\mkern 1mu} 2} \right\}.\)
Vậy \(A = \left\{ { – 2; – 1;1;2} \right\}.\)
Chọn C.
Câu 4 (TH):
Phương pháp:
Tập hợp rỗng không chứa phần tử nào.
Cách giải:
+) Xét đáp án A: \(\left\{ {\begin{array}{*{20}{l}}{x \in \mathbb{R}}\\{\left| x \right| < 1}\end{array}} \right. \Rightarrow {\rm{\;}} – 1 < x < 1\) \( \Rightarrow A = \left( { – 1;{\mkern 1mu} {\mkern 1mu} 1} \right) \ne \emptyset \)
\( \Rightarrow \) Loại đáp án A.
+) Xét đáp án B: \(6{x^2} – 7x + 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = \frac{1}{6}}\end{array}} \right.\) \( \Rightarrow A = \left\{ 1 \right\} \ne \emptyset \)
\( \Rightarrow \) Loại đáp án B.
+) Xét đáp án C: \({x^2} – 4x + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2 + \sqrt 2 }\\{x = 2 – \sqrt 2 }\end{array}} \right.\) \( \Rightarrow A = \emptyset \)
Chọn C.
Câu 5 (VD):
Phương pháp:
Thực hiện các phép toán trên tập hợp. Sử dụng trục số.
Cách giải:
+) \(A \cap B = \left( { – 3;2} \right]\)
=> A đúng.
+) \(A\backslash B = \left( { – \infty ; – 3} \right]\)

=> B sai.
+) \(A \cup B = \left( { – \infty ;5} \right]\)
=> C đúng.
+) \(B\backslash A = \left( {2;5} \right]\).
=> D đúng.
Chọn B.
Câu 6 (TH):
Phương pháp:
Cho tập hợp B có n phần tử. Số tập hợp con của B là \({2^n}\)
Cách giải:
Tập hợp \(B = \left\{ {x;{\mkern 1mu} {\mkern 1mu} y;{\mkern 1mu} {\mkern 1mu} z;{\mkern 1mu} {\mkern 1mu} 1;{\mkern 1mu} {\mkern 1mu} 5} \right\}\) có 5 phần tử.
Số tập hợp con của tập B là: \({2^5} = 32\)
Chọn D.
Câu 7 (NB):
Phương pháp:
Kí hiệu \(\exists \) đọc là “tồn tại”.
Cách giải:
Mệnh đề “\(\exists x \in \mathbb{R},\,\,{x^2} = 2\)” khẳng định rằng: “Có ít nhất một số thực mà bình phương của nó bằng 2”.
Chọn B.
Câu 8 (TH):
Phương pháp:
Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là \(ax + by + c < 0\), \(ax + by + c > 0\), \(ax + by + c \le 0\), \(ax + by + c \ge 0\), trong đó a, b, c là các số cho trước sao cho \({a^2} + {b^2} \ne 0\).
Cách giải:
Bất phương trình bậc nhất hai ẩn là \(x + y \ge 0\).
Chọn D.
Câu 9 (TH):
Phương pháp:
Thay tọa độ các điểm ở các đáp án vào bất phương trình.
Cách giải:
Thay tọa độ điểm A(1;-1) ta có: \(\left( {1 + \sqrt 3 } \right) + \left( {1 – \sqrt 3 } \right) = 2 \ge 2\) (Đúng).
Vậy điểm A thuộc miền nghiệm của bất phương trình.
Chọn A.
Câu 10 (NB):
Phương pháp:
Sử dụng định lí cosin trong tam giác: \({a^2} = {b^2} + {c^2} – 2bc.\cos A.\)
Cách giải:
\(E{F^2} = E{G^2} + F{G^2} – 2EG.FG.\cos G\) là mệnh đề đúng.
Chọn D.
Câu 11 (TH):
Phương pháp:
Áp dụng định lí Sin trong tam giác ABC: \(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow \frac{{\sin B}}{{\sin C}} = \frac{{AC}}{{AB}}\).
Cách giải:
Áp dụng định lí Sin trong tam giác ABC ta có: \(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow \frac{{\sin B}}{{\sin C}} = \frac{{AC}}{{AB}}\).
Theo giả thiết \(\frac{{\sin B}}{{\sin C}} = \sqrt 3 \Rightarrow \frac{{AC}}{{AB}} = \sqrt 3 \Rightarrow AC = \sqrt 3 AB.\)
Vậy \(AC = \sqrt 3 .2\sqrt 2 = 2\sqrt 6 .\)
Chọn D.
Câu 12 (VD):
Phương pháp:
Tính sinA.
Tính diện tích tam giác ABC: \(S = \frac{1}{2}bc.\sin A.\)
Sử dụng định lí cosin trong tam giác tính a: \({a^2} = {b^2} + {c^2} – 2bc.\cos A.\)
Sử dụng công thức tính diện tích tam giác: \(S = \frac{1}{2}a{h_a}\), từ đó tính \({h_a}\).
Cách giải:
Ta có:
\(\begin{array}{l}{\sin ^2}A + {\cos ^2}A = 1\\ \Leftrightarrow {\sin ^2}A + {\left( {\frac{3}{5}} \right)^2} = 1\\ \Leftrightarrow {\sin ^2}A = \frac{{16}}{{25}}\end{array}\)
Vì \({0^0} < A < {180^0}\) nên sinA > 0 \( \Rightarrow \sin A = \frac{4}{5}.\)
Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A. = \frac{1}{2}.7.5.\frac{4}{5} = 14.\)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} – 2bc.\cos A.\\\,\,\,\,\,\, = {7^2} + {5^2} – 2.7.5.\frac{3}{5}\\\,\,\,\,\,\, = 32\\ \Rightarrow a = 4\sqrt 2 .\end{array}\)
Lại có: \(S = \frac{1}{2}a{h_a} \Rightarrow {h_a} = \frac{{2S}}{a} = \frac{{2.14}}{{4\sqrt 2 }} = \frac{{7\sqrt 2 }}{2}.\)
Chọn C.
Câu 13 (TH):
Phương pháp:
Lập mệnh đề đảo của từng mệnh đề và xét tính đúng sai.
Cách giải:
Xét mệnh đề đảo của đáp án A: “Nếu số tự nhiên n chia hết cho 3 thì số nguyên n có tổng các chữ số bằng 9”. Mệnh đề này sai vì tổng các chữ số của n phải chia hết cho 9 thì n mới chia hết cho 9.
Xét mệnh đề đảo của đáp án B: “Nếu \({x^2} > {y^2}\) thì x > y” sai vì \({x^2} > {y^2} \Leftrightarrow \left[ \begin{array}{l}x > y\\x < – y\end{array} \right.\)
Xét mệnh đề đảo của đáp án C: “Nếu t.x = t.y thì x = y” sai với t = 0 \( \Rightarrow x,y \in \mathbb{R}\).
Chọn D.
Câu 14 (TH):
Phương pháp:
Thay tọa độ các điểm vào hệ bất phương trình.
Cách giải:
Dễ thấy các điểm \(O\left( {0;0} \right)\), \(M\left( {1;0} \right)\), \(P\left( {0;2} \right)\) không thỏa mãn bất phương trình \(x + y + 1 < 0\) nên không thỏa mãn cả hệ bất phương trình.
Chọn C.
Câu 15 (NB):
Phương pháp:
Nhớ bảng giá trị lượng giác của các góc thường dùng hoặc sử dụng máy tính cầm tay.
Cách giải:
\(\begin{array}{*{20}{l}}{B = 4{a^2}{{\sin }^2}{{45}^0} – 3{{\left( {a\tan {{45}^0}} \right)}^2} + {{\left( {2a\cos {{45}^0}} \right)}^2}}\\{B = 4{a^2}{{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2} – 3{a^2} + {{\left( {2a\frac{{\sqrt 2 }}{2}} \right)}^2}}\\{B = 4{a^2}.\frac{1}{2} – 3{a^2} + 4{a^2}.\frac{1}{2}}\\{B = {a^2}}\end{array}\)
Chọn D.
Câu 16 (TH):
Phương pháp:
Sử dụng công thức tính diện tích tam giác \(S = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} = pr\).
Cách giải:
Nửa chu vi tam giác đều cạnh a là \(p = \frac{{a + a + a}}{2} = \frac{{3a}}{2}\).
Tam giác đều cạnh a có diện tích \(S = \sqrt {\frac{{3a}}{2}\left( {\frac{{3a}}{2} – a} \right)\left( {\frac{{3a}}{2} – a} \right)\left( {\frac{{3a}}{2} – a} \right)} = \frac{{{a^2}\sqrt 3 }}{4}\).
Lại có \(S = pr \Leftrightarrow r = \frac{S}{p} = \frac{{{a^2}\sqrt 3 }}{4}:\frac{{3a}}{2} = \frac{{a\sqrt 3 }}{6}\).
Chọn C.
Câu 17 (NB):
Phương pháp:
Sử dụng hệ quả định lí Cosin trong tam giác: \(\cos C = \frac{{A{C^2} + B{C^2} – A{B^2}}}{{2AC.BC}}\).
Cách giải:
Áp dụng hệ quả định lí Cosin trong tam giác ABC ta có:
\(\begin{array}{l}\cos C = \frac{{A{C^2} + B{C^2} – A{B^2}}}{{2AC.BC}}\\ \Leftrightarrow \cos {45^0} = \frac{{{{\left( {\sqrt 3 } \right)}^2} + B{C^2} – {{\left( {\sqrt 2 } \right)}^2}}}{{2.\sqrt 3 .BC}}\\ \Leftrightarrow \sqrt 6 BC = B{C^2} + 1\\ \Leftrightarrow B{C^2} – \sqrt 6 BC + 1 = 0\\ \Leftrightarrow BC = \frac{{\sqrt 6 + \sqrt 2 }}{2}\end{array}\).
Chọn B.
Câu 18 (VDC):
Phương pháp:
Số chính phương có các chữ số tận cùng là \[0,{\rm{ }}1,{\rm{ }}4,{\rm{ }}5,{\rm{ }}6,{\rm{ }}9\]. Dùng loại trừ để đưa ra đáp án đúng.
Cách giải:
Ta có số chính phương có các chữ số tận cùng là \[0,{\rm{ }}1,{\rm{ }}4,{\rm{ }}5,{\rm{ }}6,{\rm{ }}9\]. Vì vậy
– Nhận thấy giữa mệnh đề (1) và (2) có mâu thuẫn. Bởi vì, giả sử 2 mệnh đề này đồng thời là đúng thì \(n + 8\) có chữ số tận cùng là 2 nên không thể là số chính phương. Vậy trong hai mệnh đề này phải có một mệnh đề là đúng và một mệnh đề là sai.
– Tương tự, nhận thấy giữa mệnh đề (2) và (3) cũng có mâu thuẫn. Bởi vì, giả sử mệnh đề này đồng thời là đúng thì \(n – 1\) có chữ số tận cùng là 3 nên không thể là số chính phương.
Vậy trong ba mệnh đề trên thì mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai.
Chọn D.
Câu 19 (NB):
Phương pháp:
Biểu diễn tập hợp trên trục số.
Cách giải:
Hình vẽ đã cho là minh họa cho tập hợp \(( – 3;5]\)
Chọn D.
Câu 20 (NB):
Phương pháp:
Sử dụng mối liên hệ giá trị lượng giác của hai góc bù nhau, đối nhau, phụ nhau
Cách giải:
\(\sin (\pi + \alpha ) = \sin ( – \alpha ) = – \sin \alpha .\) => A sai
\[\cos ( – \alpha ) = \cos \alpha .\] => B đúng
\(\tan (\pi – \alpha ) = – \tan \alpha \) => C đúng
\(\cot \left( {\frac{\pi }{2} – \alpha } \right) = \tan \alpha \)=> D đúng
Chọn A.
Câu 21 (TH):
Phương pháp:
\({C_B}A = B\backslash A = \{ x|x \in B\) và \(x \notin A\)}.
Cách giải:
Ta có: \({C_B}A = B\backslash A = [ – 2; + \infty ){\rm{\backslash }}( – 1;4]\)

\( \Rightarrow {C_B}A = [ – 2; – 1] \cup (4; + \infty ).\)
Chọn A.
Câu 22 (VD):
Phương pháp:
– Tính BC dựa vào định lí côsin trong tam giác cân ABC.
– Tính BM.
– Tính AM dựa vào định lí côsin trong tam giác ABM.
Cách giải:
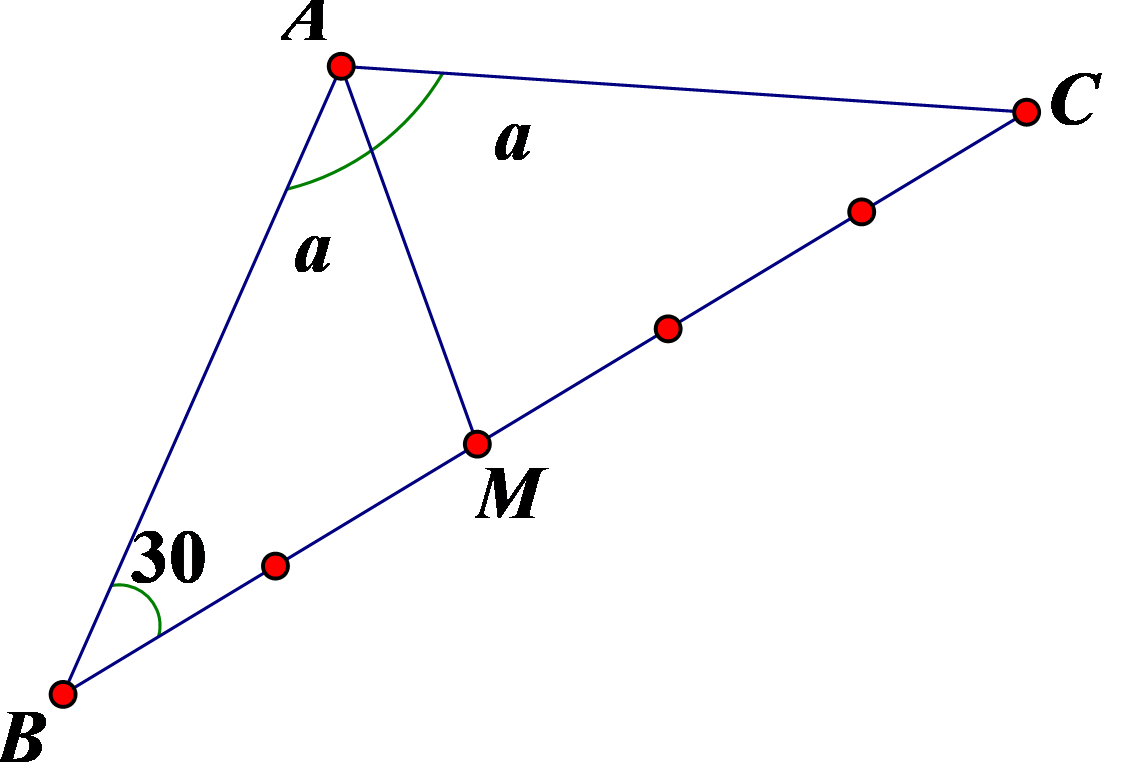
\(BC = \sqrt {A{B^2} + A{C^2} – 2ABAC\cos {{120}^0}} = \sqrt {{a^2} + {a^2} – 2a.a.\left( { – \frac{1}{2}} \right)} = a\sqrt 3 {\rm{ }} \Rightarrow BM = \frac{{2a\sqrt 3 }}{5}\)
\(AM = \sqrt {A{B^2} + B{M^2} – 2AB.BM.cos{{30}^0}} = \sqrt {{a^2} + {{\left( {\frac{{2a\sqrt 3 }}{5}} \right)}^2} – 2a.\frac{{2a\sqrt 3 }}{5}.\frac{{\sqrt 3 }}{2}} = \frac{{a\sqrt 7 }}{5}\).
Chọn C.
Câu 23 (TH):
Phương pháp:
Tìm phương trình đường thẳng d. Loại đáp án.
Thay tọa độ điểm O(0;0) vào các bất phương trình chưa bị loại ở các đáp án, tiếp tục loại đáp án.
Cách giải:
Đường thẳng d đi qua điểm (3;0) nên loại đáp án A, B.
Ta thấy điểm O(0;0) không thuộc miền nghiệm của bất phương trình.
+ Thay tọa độ điểm O(0;0) vào biểu thức \(x – 2y\) ta có: \(0 – 2.0 = 0 < 3\)
Do đó bất phươn trình cần tìm là \(x – 2y > 3\)
Chọn D.
Câu 24 (TH):
Phương pháp:
Sử dụng công thức: \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}.\)
Cách giải:
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\\ \Leftrightarrow 1 + {\left( { – 2\sqrt 2 } \right)^2} = \frac{1}{{{{\cos }^2}\alpha }}\\ \Leftrightarrow {\cos ^2}\alpha = \frac{1}{9}\\ \Leftrightarrow {\sin ^2}\alpha = 1 – \frac{1}{9} = \frac{8}{9}\\ \Leftrightarrow \sin \alpha = \pm \frac{{2\sqrt 2 }}{3}\end{array}\)
Vì \({0^0} < \alpha < {180^0}\) \( \Rightarrow \sin \alpha > 0\).
Vậy \(\sin \alpha = \frac{{2\sqrt 2 }}{3}.\)
Chọn C.
Câu 25 (VD):
Phương pháp:
Áp dụng hệ quả định lí Sin trong tam giác ABC.
Cách giải:
Ta có: \(\angle ACB = {180^0} – {45^0} – {70^0} = {65^0}\)
Áp dụng hệ quả định lí Sin trong tam giác ABC ta có:
\(\begin{array}{l}\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow \frac{{AC}}{{\sin {{70}^0}}} = \frac{{40}}{{\sin {{65}^0}}}\\ \Rightarrow AC = \frac{{40}}{{\sin {{65}^0}}}.\sin {70^0} \approx 41,47\,\,\left( m \right)\end{array}\)
Chọn C.
Câu 26 (TH):
Phương pháp:
Sai số tương đối \({\delta _a} \le \frac{d}{{\left| a \right|}}\).
Cách giải:
Ta có: \(d = \frac{1}{4} \Rightarrow \delta \le \frac{d}{{\left| a \right|}} = \frac{1}{{4.365}} = 0,0068\% \).
Chọn A.
Câu 27 (NB):
Phương pháp:
Để tìm các tứ phân vị của mẫu số liệu có n giá trị ta làm như sau:
• Sắp xếp mẫu số liệu theo thứ tự không giảm.
• Tìm trung vị. Giá trị này là Q2.
• Tìm trung vị của nửa số liệu bên trái Q2 (không bao gồm Q2 nếu n lẻ). Giá trị này là Q1.
• Tìm trung vị của nửa số liệu bên phải Q2 (không bao gồm Q2 nếu n lẻ). Giá trị này là Q3.
Q1, Q2, Q3 được gọi là các tứ phân vị của mẫu số liệu.
Cách giải:
Sắp xếp mẫu số liệu theo thứ tự không giảm: 1 3 6 8 9 12.
Cỡ mẫu n = 6 chẵn nên \({Q_2} = \frac{{6 + 8}}{2} = 7.\)
Nửa số liệu bên trái Q2: 1 3 6 => Q1 = 3.
Nửa số liệu bên phải Q2: 8 9 12 => Q3 = 9.
Vậy Q1 = 3, Q2 = 7, Q3 = 9.
Chọn D.
Câu 28 (NB):
Phương pháp:
Nhóm \(\overrightarrow {AB} ,\overrightarrow {BC} \); \(\overrightarrow {DC} ,\overrightarrow {AD} \), áp dụng quy tắc cộng vectơ.
Cách giải:
Ta có: \(\overrightarrow {AB} {\rm{ \;}} – \overrightarrow {DC} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} – \overrightarrow {AD} {\rm{ \;}} = \left( {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} } \right) – \left( {\overrightarrow {AD} {\rm{ \;}} + \overrightarrow {DC} } \right) = \overrightarrow {AC} {\rm{ \;}} – \overrightarrow {AC} {\rm{ \;}} = \vec 0\).
Chọn A.
Câu 29 (NB):
Phương pháp:
Sử dụng quy tắc hình bình hành tính \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} \).
Tính độ dài vectơ vừa tìm được.
Cách giải:
Ta có: \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {AC} } \right| = AC = a\).
Chọn A.
Câu 30 (VDC):
Phương pháp:
Áp dụng quy tắc hình bình hành.
Vật đứng yên khi tổng các lực tác động lên điểm bằng 0.
Cách giải:
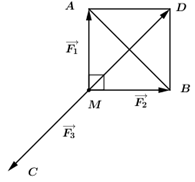
Có cường độ lực \(\overrightarrow {{F_1}} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {{F_2}} \) đều bằng 50 N và tam giác MAB vuông tại M
\( \Rightarrow \) Tam giác MAB vuông cân tại M
Lấy điểm D sao cho MADB là hình vuông
\( \Rightarrow MD = \sqrt {M{A^2} + A{D^2}} {\rm{\;}} = \sqrt {M{A^2} + M{B^2}} {\rm{\;}} = 50\sqrt 2 {\mkern 1mu} {\mkern 1mu} N\)
Vì vật đứng yên nên tổng các lực tác động lên điểm bằng 0
\( \Rightarrow \overrightarrow {{F_1}} {\rm{\;}} + \overrightarrow {{F_2}} {\rm{\;}} + \overrightarrow {{F_3}} {\rm{\;}} = \vec 0\) hay \(\overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} {\rm{\;}} + \overrightarrow {{F_3}} {\rm{\;}} = \vec 0\)
\( \Rightarrow \overrightarrow {{F_3}} {\rm{\;}} = {\rm{\;}} – \left( {\overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} } \right) = {\rm{\;}} – \overrightarrow {MD} \)
Vậy lực \(\overrightarrow {{F_3}} \) có hướng ngược với \(\overrightarrow {MD} \) và có cường độ bằng \(50\sqrt 2 {\mkern 1mu} {\mkern 1mu} N \approx 70,71{\mkern 1mu} {\mkern 1mu} N\)
Chọn C.
Câu 31 (TH):
Phương pháp:
Đối với bảng phân bố tần số, phương sai được tính theo công thức:
\({s^2} = \frac{1}{N}\left[ {{n_1}{{\left( {{x_1} – \bar x} \right)}^2} + {n_2}{{\left( {{x_2} – \bar x} \right)}^2} + {\rm{\;}} \ldots {\rm{\;}} + {n_k}{{\left( {{x_k} – \bar x} \right)}^2}} \right]\)
Với \({n_i};{\mkern 1mu} {\mkern 1mu} {f_i}\) lần lượt là tần số, tần suất của giá trị \({x_i}\).
Cách giải:
Bảng phân số tần số:

*) Sản lượng trung bình của 40 thửa ruộng là:
\(\bar x = \frac{{20.5 + 21.8 + 22.11 + 23.10 + 24.6}}{{40}} = 22,1{\mkern 1mu} \)(tạ)
*) Phương sai:
\({s^2} = \frac{1}{{40}}\left[ {5.{{\left( {20 – 22,1} \right)}^2} + 8.{{\left( {21 – 22,1} \right)}^2} + 11.{{\left( {22 – 22,1} \right)}^2} + 10.{{\left( {23 – 22,1} \right)}^2} + 6.{{\left( {24 – 22,1} \right)}^2}} \right]\)\( = 1,54\) (tạ)
Chọn B.
Câu 32 (TH):
Phương pháp:
Áp dụng quy tắc cộng vecto, quy tắc hình bình hành để biểu diễn véctơ.
Cách giải:
\(\overrightarrow {BM} {\rm{\;}} = \frac{1}{2}\left( {\overrightarrow {BA} {\rm{\;}} + \overrightarrow {BC} } \right) = \frac{1}{2}\overrightarrow {BA} {\rm{\;}} + \frac{1}{2}\overrightarrow {BC} \)
\( \Rightarrow \overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\overrightarrow {BM} {\rm{\;}} = \frac{2}{3} \cdot \left( {\frac{1}{2}\overrightarrow {BA} {\rm{\;}} + \frac{1}{2}\overrightarrow {BC} } \right) = \frac{1}{3}\overrightarrow {BA} {\rm{\;}} + \frac{1}{3}\overrightarrow {BC} \)
Mặt khác, \(\overrightarrow {BA} {\rm{\;}} = \vec a,{\mkern 1mu} {\mkern 1mu} \overrightarrow {BC} {\rm{\;}} = \vec b\) nên ta có: \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\)
Vậy \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\).
Chọn A.
Câu 33 (VD):
Phương pháp:
Áp dụng quy tắc cộng vecto để tìm được vecto \(\vec u\).
Cách giải:
Vì ABCD là hình vuông nên ta có: \(AB = BC = CD = DA = 2\); \(AC = BD = a\sqrt 2 \).
Ta có:
\(\vec u = \overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} {\rm{\;}} + \overrightarrow {MC} {\rm{\;}} – 3\overrightarrow {MD} \)
\({\mkern 1mu} = \left( {\overrightarrow {MD} {\rm{\;}} + \overrightarrow {DA} } \right) + \left( {\overrightarrow {MD} {\rm{\;}} + \overrightarrow {DB} } \right) + \left( {\overrightarrow {MD} {\rm{\;}} + \overrightarrow {DC} } \right) – 3\overrightarrow {MD} \)
\({\mkern 1mu} = \overrightarrow {MD} {\rm{\;}} + \overrightarrow {DA} {\rm{\;}} + \overrightarrow {MD} {\rm{\;}} + \overrightarrow {DB} {\rm{\;}} + \overrightarrow {MD} {\rm{\;}} + \overrightarrow {DC} {\rm{\;}} – 3\overrightarrow {MD} \)
\( = \overrightarrow {DA} {\rm{\;}} + \overrightarrow {DB} {\rm{\;}} + \overrightarrow {DC} \)
\( = \left( {\overrightarrow {DA} {\rm{\;}} + \overrightarrow {DC} } \right) + \overrightarrow {DB} \)
\( = \overrightarrow {DB} {\rm{\;}} + \overrightarrow {DB} \)
\( = 2\overrightarrow {DB} \)
\( \Rightarrow \vec u = 2\overrightarrow {DB} \)
\( \Rightarrow \left| {\vec u} \right| = \left| {2.\overrightarrow {DB} } \right| = 2.a.\sqrt 2 {\rm{\;}} = 2\sqrt 2 a\)
Chọn D.
Câu 34 (VD):
Phương pháp:
Áp dụng tích vô hướng \(\overrightarrow a .\overrightarrow b = a.b.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
Cách giải:
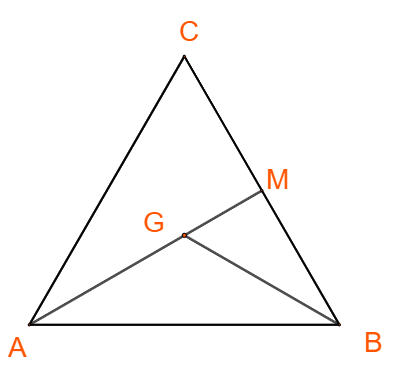
Ta có:
\(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = a.a.\cos A = {a^2}\cos {60^ \circ } = \frac{1}{2}{a^2}\) => A đúng
\(\overrightarrow {AC} .\overrightarrow {CB} = AC.CB.\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = a.a.\cos {120^ \circ } = – \frac{1}{2}{a^2}\) => B đúng
+ \(AG = \frac{2}{3}AM;AM = AC.\sin C = a.\sin {60^ \circ } = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow AG = BG = \frac{{a\sqrt 3 }}{3}\)
\(\overrightarrow {GA} .\overrightarrow {GB} = GA.GB.\cos \left( {\overrightarrow {GA} ,\overrightarrow {GB} } \right) = \frac{{a\sqrt 3 }}{3}.\frac{{a\sqrt 3 }}{3}.\cos {120^ \circ } = – \frac{1}{6}{a^2}\) => C sai.
\(\overrightarrow {AB} .\overrightarrow {AG} = AB.AG.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AG} } \right) = a.\frac{{a\sqrt 3 }}{3}.\cos {30^ \circ } = \frac{1}{2}{a^2}\) => D đúng.
Chọn C.
Câu 35 (VD):
Cách giải:
Ta có:
\(AC = BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 \)
Lại có:
\(\left\{ \begin{array}{l}\overrightarrow {BK} = \overrightarrow {BA} + \overrightarrow {AK} = \overrightarrow {BA} + \frac{1}{2}\overrightarrow {AD} \\\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \end{array} \right.\)
\(\begin{array}{l} \Rightarrow \overrightarrow {BK} .\overrightarrow {AC} = \left( {\overrightarrow {BA} + \frac{1}{2}\overrightarrow {AD} } \right).\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)\\ = \overrightarrow {BA} .\overrightarrow {AB} + \overrightarrow {BA} .\overrightarrow {AD} + \frac{1}{2}\overrightarrow {AD} .\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} .\overrightarrow {AD} \\ = – {a^2} + 0 + 0 + \frac{1}{2}{\left( {a\sqrt 2 } \right)^2}\\ = 0\end{array}\)
Chọn A.
II. Tự luận (3 điểm)
Câu 1 (TH):
Phương pháp:
Biểu diễn trên trục số.
Cách giải:
\(A \cup B = [ – 2;6)\)

\(A \cap B = [ – 1;3)\)

\(A\backslash B = [ – 2; – 1)\)

\(B\backslash A = [3;6)\)

Câu 2 (VD):
Phương pháp:
a) +) Số trung bình \(\bar x = \frac{{{x_1} + {x_2} + … + {x_n}}}{n}\).
+) Phương sai: \({s^2} = \frac{1}{n}\left( {x_1^2 + x_2^2 + … + x_n^2} \right) – {\bar x^2}\)
b) +) Khoảng tứ phân vị, kí hiệu là ΔQ, là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất, tức là
ΔQ = Q3 – Q1.
+) Giá trị ngoại lệ: Giá trị ngoại lệ x thỏa mãn x > Q3 + 1,5∆Q hoặc x < Q1 − 1,5∆Q.
Bỏ giá trị ngoại lệ (nếu có), tính lại số trung bình, tìm số trung vị của 2 mẫu số liệu và so sánh.
Cách giải:
a) n = 15.
+ Bảo Anh:
Số trung bình:
\({\bar x_1} = \frac{{2 + 4 + 3 + 4 + 6 + 2 + 3 + 2 + 4 + 5 + 3 + 4 + 6 + 7 + 3}}{{15}} = \frac{{58}}{{15}} \approx 3,87\).
Phương sai:
\(s_1^2 = \frac{1}{{15}}\left( {{{3.2}^2} + {{4.3}^2} + {{4.4}^2} + {5^2} + {{2.6}^2} + {7^2}} \right) – \bar x_1^2 = 2,25\).
+ Quang:
Số trung bình:
\({\bar x_2} = \frac{{3 + 4 + 1 + 2 + 2 + 3 + 4 + 1 + 2 + 30 + 2 + 2 + 2 + 3 + 6}}{{15}} = \frac{{67}}{{15}} \approx 4,47\)
Phương sai:
\(s_2^2 = \frac{1}{{15}}\left( {{{2.1}^2} + {{6.2}^2} + {{3.3}^2} + {{2.4}^2} + {6^2} + {{30}^2}} \right) – \bar x_2^2 = 48,12\).
b)
+ Bảo Anh:
Áp dụng các bước tìm tứ phân vị ta tìm được: Q1 = 3, Q3 = 5.
\( \Rightarrow {\Delta _Q}\) = Q3 – Q1 = 5 – 3 = 2.
Giá trị ngoại lệ x thỏa mãn
x > Q3 + 1,5∆Q = 5 + 1,5.2 = 8
Hoặc x < Q1 − 1,5∆Q = 3 − 1,5.2 = 0
Vậy đối chiếu mẫu số liệu của Khuê suy ra không có giá trị ngoại lệ.
+ Quang:
Áp dụng các bước tìm tứ phân vị ta tìm được Q1 = 2, Q3 = 4
Khi đó khoảng tứ phân vị là ∆Q = Q3 − Q1 = 4 – 2 = 2.
Giá trị ngoại lệ x thỏa mãn
x > Q3 + 1,5∆Q = 4 + 1,5.2 = 7
Hoặc x < Q1 − 1,5∆Q = 2 − 1,5.2 = −1
Vậy đối chiếu mẫu số liệu của Trọng suy ra giá trị ngoại lệ là 30.
Câu 3 (VDC):
Cách giải:
a) Gọi M là trung điểm AB.
Ta có: \(\overrightarrow {IA} + 3\overrightarrow {IB} – 2\overrightarrow {IC} = \overrightarrow 0 \)
\[\begin{array}{l} \Leftrightarrow \overrightarrow {IA} + \overrightarrow {IB} + 2\overrightarrow {IB} – 2\overrightarrow {IC} = \overrightarrow 0 \\ \Leftrightarrow 2\overrightarrow {IM} + 2\overrightarrow {CB} = \overrightarrow 0 \\ \Leftrightarrow 2\overrightarrow {IM} = 2\overrightarrow {BC} \\ \Leftrightarrow \overrightarrow {IM} = \overrightarrow {BC} \end{array}\]
Do đó IMCB là hình bình hành
Vậy I là đỉnh thứ tư của hình bình hành IMCB.
b) Ta có: \(3\overrightarrow {DB} – 2\overrightarrow {DC} = \overrightarrow 0 \)
\(\begin{array}{l} \Leftrightarrow 3\overrightarrow {DC} + 3\overrightarrow {CB} – 2\overrightarrow {DC} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {DC} + 3\overrightarrow {CB} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {CD} = 3\overrightarrow {CB} \end{array}\)
Vậy D thuộc tia CB, sao cho CD=3CB.
c)
Cách 1:
Ta có: D thuộc tia CB, sao cho CD=3CB.
\( \Rightarrow \overrightarrow {BD} = 2\overrightarrow {CB} \)\( \Rightarrow \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AB} + 2\overrightarrow {CB} \)
Lại có: \(\overrightarrow {AI} = \overrightarrow {AM} + \overrightarrow {MI} = \frac{1}{2}\overrightarrow {AB} + \overrightarrow {CB} \)
\( \Rightarrow \overrightarrow {AD} = 2\overrightarrow {AI} \)
Vậy A, I, D thẳng hàng.
Cách 2:
Gọi J là giao điểm của IM và AD.
Xét tam giác ABD ta có:
JM // DB (do IM // BC)
M là trung điểm AB
=> J là trung điểm AD và \(JM = \frac{1}{2}DB\)
Lại có: \(IM = BC = \frac{1}{3}CD \Rightarrow IM = \frac{1}{2}BD\)
Do đó \(IM = JM\) hay \(I \equiv J\)
Vậy A, I, D thẳng hàng.
Đề 6
Phần 1: Trắc nghiệm (30 câu – 6 điểm)
Câu 1: Trong các câu sau, có bao nhiêu câu là không phải là mệnh đề?
a) Huế là một thành phố của Việt Nam.
b) Sông Hương chảy ngang qua thành phố Huế.
c) Hãy trả lời câu hỏi này!
d) \(5 + 19 = 24.\)
e) \(6 + 81 = 25.\)
f) Bạn có mang theo máy tính không?
g) \(x + 2 = 11.\)
A. 1. B. 2. C. 3. D. 4.
Câu 2: Hãy viết số quy tròn của số gần đúng \(a = 17658\) biết \(\bar a = 17658\,\, \pm \,\,16.\)
A. 17700. B. 17800. C. 17500. D. 17600.
Câu 3: Cho hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Đẳng thức nào sau đây sai?
A. \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \vec 0.\) B. \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .\)
C. \(\left| {\overrightarrow {BA} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {DA} + \overrightarrow {DC} } \right|.\) D. \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AB} + \overrightarrow {CB} .\)
Câu 4: Lớp 10E có \(7\) học sinh giỏi Toán, \(5\) học sinh giỏi Lý, \(6\) học sinh giỏi Hóa, \(3\) học sinh giỏi cả Toán và Lý, \(4\) học sinh giỏi cả Toán và Hóa, \(2\) học sinh giỏi cả Lý và Hóa, \(1\) học sinh giỏi cả \(3\) môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10E là
A. \(9.\) B. \(10.\) C. \(18.\) D. \(28.\)
Câu 5: Miền nghiệm của bất phương trình: \(3x + 2\left( {y + 3} \right) > 4\left( {x + 1} \right) – y + 3\) là nửa mặt phẳng chứa điểm:
A. \(\left( {3;0} \right).\) B. \(\left( {3;1} \right).\) C. \(\left( {2;1} \right).\) D. \(\left( {0;0} \right).\)
Câu 6: Phần không tô đậm trong hình vẽ dưới đây (không chứa biên), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
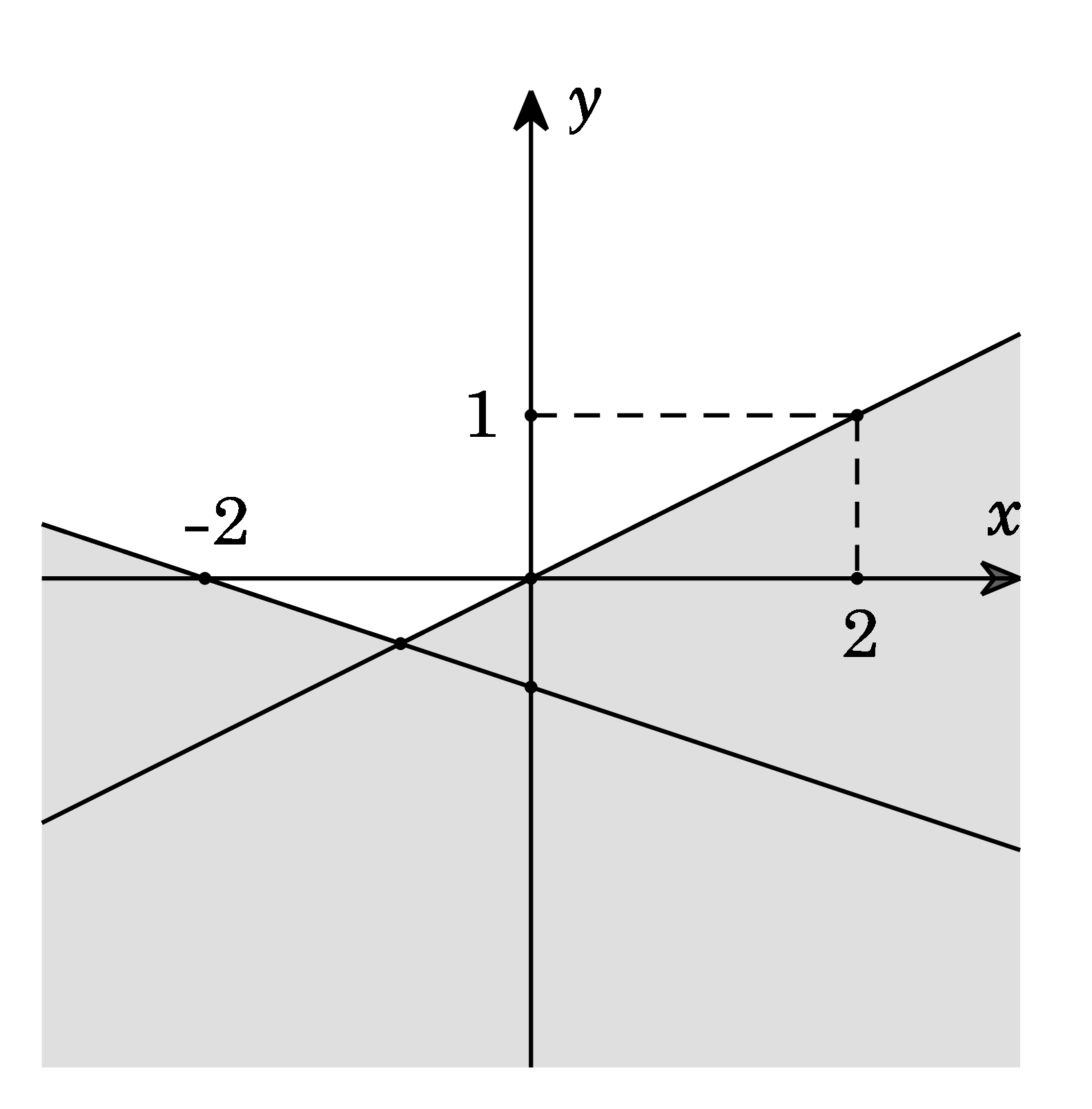
A. \(\left\{ \begin{array}{l}x – 2y \le 0\\x + 3y \ge – 2\end{array} \right..\) B. \(\left\{ \begin{array}{l}x – 2y > 0\\x + 3y < – 2\end{array} \right..\) C. \(\left\{ \begin{array}{l}x – 2y \le 0\\x + 3y \le – 2\end{array} \right..\) D. \(\left\{ \begin{array}{l}x – 2y < 0\\x + 3y > – 2\end{array} \right..\)
Câu 7: Tam giác \(ABC\) có \(AB = 3,{\rm{ }}AC = 6\) và \(\widehat A = 60^\circ \). Tính bán kính \(R\) của đường tròn ngoại tiếp tam giác \(ABC\).
A. \(R = 3\). B. \(R = 3\sqrt 3 \). C. \(R = \sqrt 3 \). D. \(R = 6\).
Câu 8: Hai chiếc tàu thủy cùng xuất phát từ một vị trí \(A\), đi thẳng theo hai hướng tạo với nhau góc \({60^0}\). Tàu \(B\) chạy với tốc độ \(20\) hải lí một giờ. Tàu \(C\) chạy với tốc độ \(15\) hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?
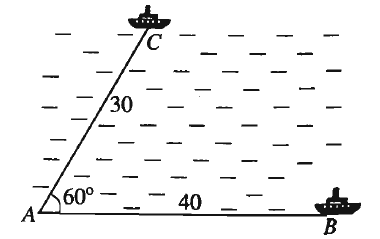
Kết quả gần nhất với số nào sau đây?
A. \(61\) hải lí.
B. \(36\) hải lí.
C. \(21\) hải lí.
D. \(18\) hải lí.
Câu 9: Tính giá trị biểu thức \(S = {\sin ^2}15^\circ + {\cos ^2}20^\circ + {\sin ^2}75^\circ + {\cos ^2}110^\circ \).
A. \(S = 0.\) B. \(S = 1.\) C. \(S = 2.\) D. \(S = 4.\)
Câu 10: Cho hình vuông \(ABCD\) cạnh \(a\). Tính \(P = \overrightarrow {AC} .\left( {\overrightarrow {CD} + \overrightarrow {CA} } \right).\)
A. \(P = – 1.\) B. \(P = 3{a^2}.\) C. \(P = – 3{a^2}.\) D. \(P = 2{a^2}.\)
Câu 11: Có 100 học sinh dự thi học sinh giỏi Toán (điểm 20). Kết quả như sau:

Nhận xét nào sau đây là đúng?
A. Phương sai lớn hơn 4, độ lệch chuẩn lớn hơn 2
B. Phương sai lớn hơn 5, độ lệch chuẩn lớn hơn 2
C. Phương sai nhỏ hơn 5, độ lệch chuẩn lớn hơn 2
D. Phương sai nhỏ hơn 4, độ lệch chuẩn nhỏ hơn 2
Câu 12: Cho tam giác ABC. Trên cạnh BC lấy điểm \(D\) sao cho \(\overrightarrow {BD} {\rm{\;}} = \frac{1}{3}\overrightarrow {BC} \). Khi đó, vectơ \(\overrightarrow {AD} \) bằng
A. \(\frac{2}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \) B. \(\frac{1}{3}\overrightarrow {AB} {\rm{\;}} + \frac{2}{3}\overrightarrow {AC} \) C. \(\overrightarrow {AB} {\rm{\;}} + \frac{2}{3}\overrightarrow {AC} \) D. \(\frac{5}{3}\overrightarrow {AB} {\rm{\;}} – \frac{1}{3}\overrightarrow {AC} \)
Câu 13: Gọi \(G\) là trọng tâm của \(\Delta ABC\). Đặt \(\overrightarrow {GA} {\rm{\;}} = \vec a;\overrightarrow {GB} {\rm{\;}} = \vec b\). Xác định giá trị của \(m,{\mkern 1mu} {\mkern 1mu} n\) để \(\overrightarrow {BC} {\rm{\;}} = m\vec a + n\vec b\).
A. \(m = 1,{\mkern 1mu} {\mkern 1mu} n = 2\) B. \(m = {\rm{\;}} – 1,{\mkern 1mu} {\mkern 1mu} n = {\rm{\;}} – 2\) C. \(m = 2,{\mkern 1mu} {\mkern 1mu} n = 1\) D. \(m = {\rm{\;}} – 2,{\mkern 1mu} {\mkern 1mu} n = {\rm{\;}} – 1\)
Câu 14: Tam giác \(ABC\) có \(AC = 4,{\rm{ }}\widehat {BAC} = 30^\circ ,{\rm{ }}\widehat {ACB} = 75^\circ \). Tính diện tích tam giác \(ABC\).
A. \({S_{\Delta ABC}} = 8\). B. \({S_{\Delta ABC}} = 4\sqrt 3 \). C. \({S_{\Delta ABC}} = 4\). D. \({S_{\Delta ABC}} = 8\sqrt 3 \).
Câu 15: Độ lệch chuẩn đo mức độ phân tán của các số liệu trong mẫu quanh:
A. Số mốt. B. Số trung vị. C. Số trung bình. D. Phương sai.
Câu 16: Sản lượng lúa của 40 thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng tần số sau đây: (đơn vị: tạ)

Độ lệch chuẩn là
A. 1,24 B. 1,54 C. 22,1 D. 4,70
Câu 17: Cho tập hợp \(A = {\rm{\{ }}x \in \mathbb{N}\left| x \right.\) là ước chung của \(36\;{\rm{v\`a }}\;{\rm{120\} }}\). Hãy liệt kê các phần tử của tập hợp \(A\).
A. \(A = \left\{ {1;2;3;4;6;12} \right\}.\) B. \(A = \left\{ {1;2;4;6;8;12} \right\}.\)
C. \(A = \left\{ {2;4;6;8;10;12} \right\}.\)
 HỌC NGAY
Môn Toán học Lớp 12SGK Toán lớp 12 SGK Toán 12 Nâng cao SBT Toán lớp 12 SBT Toán lớp 12 Nâng cao Đề thi, đề kiểm tra Toán lớp 12 SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diềuMôn Ngữ văn Lớp 12Soạn văn 12 siêu ngắn Soạn văn 12 chi tiết Tác giả – Tác phẩm lớp 12 Văn mẫu 12 Luyện dạng đọc hiểu Đề thi, đề kiểm tra Ngữ Văn 12 mới Bài tập trắc nghiệm Văn 12 Soạn văn – Kết nối tri thức Soạn văn – Cánh diều Xem thêmMôn Tiếng Anh Lớp 12Bài tập trắc nghiệm Tiếng Anh 12 mới Bài tập trắc nghiệm Tiếng Anh 12 Đề thi, đề kiểm tra Tiếng Anh 12 mới Tiếng Anh – Global Success Tiếng Anh – Friends Global Tiếng Anh – iLearn Smart World Tiếng Anh – Bright Tiếng Anh – English Discovery SGK Tiếng Anh 12 Mới Xem thêmMôn Vật lí Lớp 12SGK Vật lí lớp 12 SGK Vật lí lớp 12 Nâng cao SBT Vật lí lớp 12 Bài tập trắc nghiệm Lí 12 Đề thi, kiểm tra Lí lớp 12 SGK Vật Lí – Kết nối tri thức SGK Vật Lí – Cánh diều SGK Vật Lí – Chân trời sáng tạoMôn Hóa học Lớp 12SGK Hóa lớp 12 SGK Hóa học lớp 12 Nâng cao SBT Hóa lớp 12 Bài tập trắc nghiệm Hóa 12 Đề thi, đề kiểm tra Hóa lớp 12 SGK Hóa – Kết nối tri thức SGK Hóa – Cánh diều SGK Hóa – Chân trời sáng tạoMôn Sinh học Lớp 12SGK Sinh lớp 12 SGK Sinh lớp 12 Nâng cao SBT Sinh lớp 12 Bài tập trắc nghiệm Sinh 12 Đề thi, đề kiểm tra Sinh lớp 12 SGK Sinh – Kết nối tri thức SGK Sinh – Cánh diều SGK Sinh – Chân trời sáng tạoMôn Lịch sử Lớp 12Tập bản đồ Lịch sử lớp 12 Đề thi, đề kiểm tra Lịch sử 12 SGK Lịch sử lớp 12 SBT Lịch sử lớp 12Môn Địa lí Lớp 12SGK Địa lí lớp 12 SBT Địa lí lớp 12 Tập bản đồ Địa lí lớp 12 Đề thi, kiểm tra Địa lí lớp 12Môn GDCD Lớp 12SGK GDCDMôn Công nghệ Lớp 12SGK Công nghệ 12Môn Tin học Lớp 12SGK Tin học lớp 12
HỌC NGAY
Môn Toán học Lớp 12SGK Toán lớp 12 SGK Toán 12 Nâng cao SBT Toán lớp 12 SBT Toán lớp 12 Nâng cao Đề thi, đề kiểm tra Toán lớp 12 SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diềuMôn Ngữ văn Lớp 12Soạn văn 12 siêu ngắn Soạn văn 12 chi tiết Tác giả – Tác phẩm lớp 12 Văn mẫu 12 Luyện dạng đọc hiểu Đề thi, đề kiểm tra Ngữ Văn 12 mới Bài tập trắc nghiệm Văn 12 Soạn văn – Kết nối tri thức Soạn văn – Cánh diều Xem thêmMôn Tiếng Anh Lớp 12Bài tập trắc nghiệm Tiếng Anh 12 mới Bài tập trắc nghiệm Tiếng Anh 12 Đề thi, đề kiểm tra Tiếng Anh 12 mới Tiếng Anh – Global Success Tiếng Anh – Friends Global Tiếng Anh – iLearn Smart World Tiếng Anh – Bright Tiếng Anh – English Discovery SGK Tiếng Anh 12 Mới Xem thêmMôn Vật lí Lớp 12SGK Vật lí lớp 12 SGK Vật lí lớp 12 Nâng cao SBT Vật lí lớp 12 Bài tập trắc nghiệm Lí 12 Đề thi, kiểm tra Lí lớp 12 SGK Vật Lí – Kết nối tri thức SGK Vật Lí – Cánh diều SGK Vật Lí – Chân trời sáng tạoMôn Hóa học Lớp 12SGK Hóa lớp 12 SGK Hóa học lớp 12 Nâng cao SBT Hóa lớp 12 Bài tập trắc nghiệm Hóa 12 Đề thi, đề kiểm tra Hóa lớp 12 SGK Hóa – Kết nối tri thức SGK Hóa – Cánh diều SGK Hóa – Chân trời sáng tạoMôn Sinh học Lớp 12SGK Sinh lớp 12 SGK Sinh lớp 12 Nâng cao SBT Sinh lớp 12 Bài tập trắc nghiệm Sinh 12 Đề thi, đề kiểm tra Sinh lớp 12 SGK Sinh – Kết nối tri thức SGK Sinh – Cánh diều SGK Sinh – Chân trời sáng tạoMôn Lịch sử Lớp 12Tập bản đồ Lịch sử lớp 12 Đề thi, đề kiểm tra Lịch sử 12 SGK Lịch sử lớp 12 SBT Lịch sử lớp 12Môn Địa lí Lớp 12SGK Địa lí lớp 12 SBT Địa lí lớp 12 Tập bản đồ Địa lí lớp 12 Đề thi, kiểm tra Địa lí lớp 12Môn GDCD Lớp 12SGK GDCDMôn Công nghệ Lớp 12SGK Công nghệ 12Môn Tin học Lớp 12SGK Tin học lớp 12 HỌC NGAY
Môn Toán học Lớp 11SGK Toán – Kết nối tri thức SGK Toán – Cánh diều SGK Toán – Chân trời sáng tạo SGK Toán 11 – Cùng khám phá Chuyên đề học tập Toán – Kết nối tri thức Chuyên đề học tập Toán – Cánh diều Chuyên đề học tập Toán – Chân trời sáng tạo SBT Toán – Kết nối tri thức SBT Toán – Cánh diều Xem thêmMôn Ngữ văn Lớp 11Văn mẫu – Kết nối tri thức Văn mẫu – Cánh diều Văn mẫu – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Kết nối tri thức Đề thi, đề kiểm tra Văn – Cánh diều Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Tóm tắt, bố cục Văn – Kết nối tri thức Tóm tắt, bố cục Văn – Cánh diều Tóm tắt, bố cục Văn – Chân trời sáng tạo Xem thêmMôn Tiếng Anh Lớp 11Đề thi, đề kiểm tra Tiếng Anh – Friends Global Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Bright Đề thi, đề kiểm tra Tiếng Anh – English Discovery SBT Tiếng Anh lớp 11 mới Đề thi, đề kiểm tra Tiếng Anh 11 mới Lý thuyết Tiếng Anh 11 Bài tập trắc nghiệm Tiếng Anh – Friends Global Bài tập trắc nghiệm Tiếng Anh – iLearn Smart World Xem thêmMôn Vật lí Lớp 11Bài tập trắc nghiệm Lí – Cánh diều Bài tập trắc nghiệm Lí – Chân trời sáng tạo SGK Vật Lí – Kết nối tri thức SGK Vật Lí – Cánh diều SGK Vật Lí – Chân trời sáng tạo Chuyên đề học tập Lí – Kết nối tri thức Chuyên đề học tập Lí – Cánh diều Chuyên đề học tập Lí – Chân trời sáng tạo SBT Vật lí – Kết nối tri thức Xem thêmMôn Hóa học Lớp 11Bài tập trắc nghiệm Hóa – Cánh diều Bài tập trắc nghiệm Hóa – Chân trời sáng tạo SBT Hóa – Chân trời sáng tạo Lý thuyết Hóa 11 Đề thi, kiểm tra Hóa – Kết nối tri thức Đề thi, kiểm tra Hóa – Cánh diều Đề thi, kiểm tra Hóa – Chân trời sáng tạo Bài tập trắc nghiệm Hóa – Kết nối tri thức SGK Hóa học – Kết nối tri thức Xem thêmMôn Sinh học Lớp 11Bài tập trắc nghiệm Sinh – Cánh diều Bài tập trắc nghiệm Sinh – Chân trời sáng tạo SGK Sinh – Kết nối tri thức SGK Sinh – Cánh diều SGK Sinh – Chân trời sáng tạo Chuyên đề học tập Sinh – Kết nối tri thức Chuyên đề học tập Sinh – Cánh diều Chuyên đề học tập Sinh – Chân trời sáng tạo SBT Sinh – Kết nối tri thức Xem thêmMôn Lịch sử Lớp 11SGK Lịch sử – Kết nối tri thức SGK Lịch sử – Chân trời sáng tạo SGK Lịch sử – Cánh diều Đề thi, kiểm tra Lịch sử lớp 11Môn Địa lí Lớp 11SGK Địa lí – Kết nối tri thức SGK Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Địa lí lớp 11 SGK Địa lí – Cánh diềuMôn GD kinh tế và pháp luật Lớp 11SGK Giáo dục kinh tế và pháp luật – Kết nối tri thức SGK Giáo dục kinh tế và pháp luật – Chân trời sáng tạo SGK Giáo dục kinh tế và pháp luật – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 11SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 11SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diềuMôn GD Quốc phòng và An ninh Lớp 11SGK Giáo dục quốc phòng và an ninh – Kết nối tri thức SGK Giáo dục quốc phòng và an ninh – Cánh diều
HỌC NGAY
Môn Toán học Lớp 11SGK Toán – Kết nối tri thức SGK Toán – Cánh diều SGK Toán – Chân trời sáng tạo SGK Toán 11 – Cùng khám phá Chuyên đề học tập Toán – Kết nối tri thức Chuyên đề học tập Toán – Cánh diều Chuyên đề học tập Toán – Chân trời sáng tạo SBT Toán – Kết nối tri thức SBT Toán – Cánh diều Xem thêmMôn Ngữ văn Lớp 11Văn mẫu – Kết nối tri thức Văn mẫu – Cánh diều Văn mẫu – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Kết nối tri thức Đề thi, đề kiểm tra Văn – Cánh diều Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Tóm tắt, bố cục Văn – Kết nối tri thức Tóm tắt, bố cục Văn – Cánh diều Tóm tắt, bố cục Văn – Chân trời sáng tạo Xem thêmMôn Tiếng Anh Lớp 11Đề thi, đề kiểm tra Tiếng Anh – Friends Global Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Bright Đề thi, đề kiểm tra Tiếng Anh – English Discovery SBT Tiếng Anh lớp 11 mới Đề thi, đề kiểm tra Tiếng Anh 11 mới Lý thuyết Tiếng Anh 11 Bài tập trắc nghiệm Tiếng Anh – Friends Global Bài tập trắc nghiệm Tiếng Anh – iLearn Smart World Xem thêmMôn Vật lí Lớp 11Bài tập trắc nghiệm Lí – Cánh diều Bài tập trắc nghiệm Lí – Chân trời sáng tạo SGK Vật Lí – Kết nối tri thức SGK Vật Lí – Cánh diều SGK Vật Lí – Chân trời sáng tạo Chuyên đề học tập Lí – Kết nối tri thức Chuyên đề học tập Lí – Cánh diều Chuyên đề học tập Lí – Chân trời sáng tạo SBT Vật lí – Kết nối tri thức Xem thêmMôn Hóa học Lớp 11Bài tập trắc nghiệm Hóa – Cánh diều Bài tập trắc nghiệm Hóa – Chân trời sáng tạo SBT Hóa – Chân trời sáng tạo Lý thuyết Hóa 11 Đề thi, kiểm tra Hóa – Kết nối tri thức Đề thi, kiểm tra Hóa – Cánh diều Đề thi, kiểm tra Hóa – Chân trời sáng tạo Bài tập trắc nghiệm Hóa – Kết nối tri thức SGK Hóa học – Kết nối tri thức Xem thêmMôn Sinh học Lớp 11Bài tập trắc nghiệm Sinh – Cánh diều Bài tập trắc nghiệm Sinh – Chân trời sáng tạo SGK Sinh – Kết nối tri thức SGK Sinh – Cánh diều SGK Sinh – Chân trời sáng tạo Chuyên đề học tập Sinh – Kết nối tri thức Chuyên đề học tập Sinh – Cánh diều Chuyên đề học tập Sinh – Chân trời sáng tạo SBT Sinh – Kết nối tri thức Xem thêmMôn Lịch sử Lớp 11SGK Lịch sử – Kết nối tri thức SGK Lịch sử – Chân trời sáng tạo SGK Lịch sử – Cánh diều Đề thi, kiểm tra Lịch sử lớp 11Môn Địa lí Lớp 11SGK Địa lí – Kết nối tri thức SGK Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Địa lí lớp 11 SGK Địa lí – Cánh diềuMôn GD kinh tế và pháp luật Lớp 11SGK Giáo dục kinh tế và pháp luật – Kết nối tri thức SGK Giáo dục kinh tế và pháp luật – Chân trời sáng tạo SGK Giáo dục kinh tế và pháp luật – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 11SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 11SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diềuMôn GD Quốc phòng và An ninh Lớp 11SGK Giáo dục quốc phòng và an ninh – Kết nối tri thức SGK Giáo dục quốc phòng và an ninh – Cánh diều HỌC NGAY
Môn Toán học Lớp 10SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Chuyên đề học tập Toán – Kết nối tri thức Chuyên đề học tập Toán – Chân trời sáng tạo Chuyên đề học tập Toán – Cánh diều Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Lý thuyết Toán 10 Xem thêmMôn Ngữ văn Lớp 10Chuyên đề học tập Văn – Chân trời sáng tạo Chuyên đề học tập Văn – Cánh diều Soạn văn – Kết nối tri thức – siêu ngắn Đề thi, đề kiểm tra Văn – Kết nối tri thức Soạn văn – Kết nối tri thức – chi tiết Đề thi, đề kiểm tra Văn – Cánh diều Soạn văn – Chân trời sáng tạo – siêu ngắn Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Soạn văn – Chân trời sáng tạo – chi tiết Xem thêmMôn Tiếng Anh Lớp 10Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Global Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Tiếng Anh – Friends Global Đề thi, đề kiểm tra Tiếng Anh – Bright Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – English Discovery Tiếng Anh – English Discovery Xem thêmMôn Vật lí Lớp 10Chuyên đề học tập Lí – Chân trời sáng tạo Lý thuyết Vật lí 10 SBT Vật lí – Chân trời sáng tạo SBT Vật lí – Cánh diều Bài tập trắc nghiệm Lí – Kết nối tri thức Bài tập trắc nghiệm Lí – Chân trời sáng tạo Bài tập trắc nghiệm Lí – Cánh diều Đề thi, đề kiểm tra Vật lí – Chân trời sáng tạo Đề thi, đề kiểm tra Vật lí – Kết nối tri thức Xem thêmMôn Hóa học Lớp 10Đề thi, kiểm tra Hóa – Cánh diều Lý thuyết Hóa 10 SGK Hóa – Kết nối tri thức SGK Hóa – Chân trời sáng tạo SGK Hóa – Cánh diều SBT Hóa – Kết nối tri thức SBT Hóa – Chân trời sáng tạo SBT Hóa 10 – Cánh diều Chuyên đề học tập Hóa – Kết nối tri thức Xem thêmMôn Sinh học Lớp 10Lý thuyết Sinh 10 SBT Sinh – Chân trời sáng tạo SBT Sinh – Cánh diều Chuyên đề học tập Sinh – Kết nối tri thức Chuyên đề học tập Sinh – Chân trời sáng tạo Bài tập trắc nghiệm Sinh – Kết nối tri thức Bài tập trắc nghiệm Sinh – Chân trời sáng tạo Bài tập trắc nghiệm Sinh – Cánh diều Đề thi, kiểm tra Sinh – Kết nối tri thức Xem thêmMôn Lịch sử Lớp 10SGK Lịch sử – Kết nối tri thức SGK Lịch sử – Chân trời sáng tạo SGK Lịch sử – Cánh Diều SBT Lịch sử – Kết nối tri thức SBT Lịch sử – Chân trời sáng tạo SBT Lịch sử – Cánh Diều Chuyên đề học tập Lịch sử – Kết nối tri thức Đề thi, đề kiểm tra Lịch sử – Kết nối tri thức Đề thi, đề kiểm tra Lịch sử lớp 10 – Chân trời sáng tạo Xem thêmMôn Địa lí Lớp 10SGK Địa lí – Kết nối tri thức SGK Địa lí – Cánh Diều SGK Địa lí – Chân trời sáng tạo SBT Địa lí – Kết nối tri thức SBT Địa lí – Chân trời sáng tạo Đề thi, đề kiểm tra Địa lí – Kết nối tri thức Đề thi, đề kiểm tra Địa lí lớp 10 – Chân trời sáng tạo Đề thi, đề kiểm tra Địa lí – Kết nối tri thứcMôn GDCD Lớp 10SGK Giáo dục kinh tế và pháp luật – KNTT SGK Giáo dục kinh tế và pháp luật – CTST SGK Giáo dục kinh tế và pháp luật – Cánh diềuMôn Tin học Lớp 10SGK Tin học – Kết nối tri thức SGK Tin học – Cánh Diều SBT Tin học – Kết nối tri thứcMôn HĐ trải nghiệm, hướng nghiệp Lớp 10SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh DiềuMôn Giáo dục thể chất Lớp 10SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diềuMôn GD Quốc phòng và An ninh Lớp 10SGK Giáo dục quốc phòng và an ninh – Kết nối tri thức SGK Giáo dục quốc phòng và an ninh – Cánh diều
HỌC NGAY
Môn Toán học Lớp 10SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Chuyên đề học tập Toán – Kết nối tri thức Chuyên đề học tập Toán – Chân trời sáng tạo Chuyên đề học tập Toán – Cánh diều Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Lý thuyết Toán 10 Xem thêmMôn Ngữ văn Lớp 10Chuyên đề học tập Văn – Chân trời sáng tạo Chuyên đề học tập Văn – Cánh diều Soạn văn – Kết nối tri thức – siêu ngắn Đề thi, đề kiểm tra Văn – Kết nối tri thức Soạn văn – Kết nối tri thức – chi tiết Đề thi, đề kiểm tra Văn – Cánh diều Soạn văn – Chân trời sáng tạo – siêu ngắn Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Soạn văn – Chân trời sáng tạo – chi tiết Xem thêmMôn Tiếng Anh Lớp 10Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Global Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Tiếng Anh – Friends Global Đề thi, đề kiểm tra Tiếng Anh – Bright Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – English Discovery Tiếng Anh – English Discovery Xem thêmMôn Vật lí Lớp 10Chuyên đề học tập Lí – Chân trời sáng tạo Lý thuyết Vật lí 10 SBT Vật lí – Chân trời sáng tạo SBT Vật lí – Cánh diều Bài tập trắc nghiệm Lí – Kết nối tri thức Bài tập trắc nghiệm Lí – Chân trời sáng tạo Bài tập trắc nghiệm Lí – Cánh diều Đề thi, đề kiểm tra Vật lí – Chân trời sáng tạo Đề thi, đề kiểm tra Vật lí – Kết nối tri thức Xem thêmMôn Hóa học Lớp 10Đề thi, kiểm tra Hóa – Cánh diều Lý thuyết Hóa 10 SGK Hóa – Kết nối tri thức SGK Hóa – Chân trời sáng tạo SGK Hóa – Cánh diều SBT Hóa – Kết nối tri thức SBT Hóa – Chân trời sáng tạo SBT Hóa 10 – Cánh diều Chuyên đề học tập Hóa – Kết nối tri thức Xem thêmMôn Sinh học Lớp 10Lý thuyết Sinh 10 SBT Sinh – Chân trời sáng tạo SBT Sinh – Cánh diều Chuyên đề học tập Sinh – Kết nối tri thức Chuyên đề học tập Sinh – Chân trời sáng tạo Bài tập trắc nghiệm Sinh – Kết nối tri thức Bài tập trắc nghiệm Sinh – Chân trời sáng tạo Bài tập trắc nghiệm Sinh – Cánh diều Đề thi, kiểm tra Sinh – Kết nối tri thức Xem thêmMôn Lịch sử Lớp 10SGK Lịch sử – Kết nối tri thức SGK Lịch sử – Chân trời sáng tạo SGK Lịch sử – Cánh Diều SBT Lịch sử – Kết nối tri thức SBT Lịch sử – Chân trời sáng tạo SBT Lịch sử – Cánh Diều Chuyên đề học tập Lịch sử – Kết nối tri thức Đề thi, đề kiểm tra Lịch sử – Kết nối tri thức Đề thi, đề kiểm tra Lịch sử lớp 10 – Chân trời sáng tạo Xem thêmMôn Địa lí Lớp 10SGK Địa lí – Kết nối tri thức SGK Địa lí – Cánh Diều SGK Địa lí – Chân trời sáng tạo SBT Địa lí – Kết nối tri thức SBT Địa lí – Chân trời sáng tạo Đề thi, đề kiểm tra Địa lí – Kết nối tri thức Đề thi, đề kiểm tra Địa lí lớp 10 – Chân trời sáng tạo Đề thi, đề kiểm tra Địa lí – Kết nối tri thứcMôn GDCD Lớp 10SGK Giáo dục kinh tế và pháp luật – KNTT SGK Giáo dục kinh tế và pháp luật – CTST SGK Giáo dục kinh tế và pháp luật – Cánh diềuMôn Tin học Lớp 10SGK Tin học – Kết nối tri thức SGK Tin học – Cánh Diều SBT Tin học – Kết nối tri thứcMôn HĐ trải nghiệm, hướng nghiệp Lớp 10SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh DiềuMôn Giáo dục thể chất Lớp 10SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diềuMôn GD Quốc phòng và An ninh Lớp 10SGK Giáo dục quốc phòng và an ninh – Kết nối tri thức SGK Giáo dục quốc phòng và an ninh – Cánh diều HỌC NGAY
Môn Toán học Lớp 9SGK Toán lớp 9 SBT Toán lớp 9 Vở bài tập Toán 9 Bài tập trắc nghiệm Toán 9 Tài liệu Dạy – học Toán 9 Đề thi, đề kiểm tra Toán lớp 9 Đề thi vào 10 môn Toán SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo Xem thêmMôn Ngữ văn Lớp 9Soạn văn 9 siêu ngắn Soạn văn 9 chi tiết Tác giả – Tác phẩm văn 9 Văn mẫu lớp 9 Vở bài tập Ngữ văn lớp 9 Bài tập trắc nghiệm Văn 9 Đề thi vào 10 môn Văn Đề thi, đề kiểm tra Văn 9 Soạn văn – Kết nối tri thức Xem thêmMôn Tiếng Anh Lớp 9Tiếng Anh – Friends Plus Tiếng Anh – iLearn Smart World Tiếng Anh – Right on! Tiếng Anh – English Discovery SGK Tiếng Anh lớp 9 Mới SGK Tiếng Anh lớp 9 SBT Tiếng Anh lớp 9 mới Vở bài tập Tiếng Anh 9 Bài tập trắc nghiệm Tiếng Anh 9 mới Xem thêmMôn Vật lí Lớp 9SGK Vật lí lớp 9 SBT Vật lí lớp 9 Vở bài tập Vật lí 9 Bài tập trắc nghiệm Lí 9 Tài liệu Dạy – Học Vật lí 9 Đề thi, kiểm tra Lí lớp 9Môn Hóa học Lớp 9SGK Hóa lớp 9 SBT Hóa lớp 9 Vở bài tập Hoá học 9 Bài tập trắc nghiệm Hóa 9 Tài liệu Dạy – học Hóa học 9 Đề thi, đề kiểm tra Hóa lớp 9Môn Sinh học Lớp 9SGK Sinh lớp 9 SBT Sinh lớp 9 Vở bài tập Sinh học 9 Đề thi, đề kiểm tra Sinh lớp 9 Bài tập trắc nghiệm Sinh 9 Đề thi, đề kiểm tra Sinh lớp 9Môn Lịch sử Lớp 9SGK Lịch sử lớp 9 VBT Lịch sử lớp 9 Tập bản đồ Lịch sử lớp 9 SBT Lịch sử lớp 9 Đề thi, kiểm tra Lịch sử lớp 9Môn Địa lí Lớp 9Đề thi, kiểm tra Địa lí lớp 9 SGK Địa lí lớp 9 SBT Địa lí lớp 9 VBT Địa lí lớp 9 Tập bản đồ Địa lí lớp 9Môn Công nghệ Lớp 9SGK Công nghệ 9Môn Tin học Lớp 9SGK Tin học lớp 9Môn Khoa học tự nhiên Lớp 9SGK Khoa học tự nhiên – Cánh diều SGK Khoa học tự nhiên – Chân trời sáng tạo SGK Khoa học tự nhiên – Kết nối tri thứcMôn Âm nhạc và mỹ thuật Lớp 9Âm nhạc và mỹ thuật lớp 9
HỌC NGAY
Môn Toán học Lớp 9SGK Toán lớp 9 SBT Toán lớp 9 Vở bài tập Toán 9 Bài tập trắc nghiệm Toán 9 Tài liệu Dạy – học Toán 9 Đề thi, đề kiểm tra Toán lớp 9 Đề thi vào 10 môn Toán SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo Xem thêmMôn Ngữ văn Lớp 9Soạn văn 9 siêu ngắn Soạn văn 9 chi tiết Tác giả – Tác phẩm văn 9 Văn mẫu lớp 9 Vở bài tập Ngữ văn lớp 9 Bài tập trắc nghiệm Văn 9 Đề thi vào 10 môn Văn Đề thi, đề kiểm tra Văn 9 Soạn văn – Kết nối tri thức Xem thêmMôn Tiếng Anh Lớp 9Tiếng Anh – Friends Plus Tiếng Anh – iLearn Smart World Tiếng Anh – Right on! Tiếng Anh – English Discovery SGK Tiếng Anh lớp 9 Mới SGK Tiếng Anh lớp 9 SBT Tiếng Anh lớp 9 mới Vở bài tập Tiếng Anh 9 Bài tập trắc nghiệm Tiếng Anh 9 mới Xem thêmMôn Vật lí Lớp 9SGK Vật lí lớp 9 SBT Vật lí lớp 9 Vở bài tập Vật lí 9 Bài tập trắc nghiệm Lí 9 Tài liệu Dạy – Học Vật lí 9 Đề thi, kiểm tra Lí lớp 9Môn Hóa học Lớp 9SGK Hóa lớp 9 SBT Hóa lớp 9 Vở bài tập Hoá học 9 Bài tập trắc nghiệm Hóa 9 Tài liệu Dạy – học Hóa học 9 Đề thi, đề kiểm tra Hóa lớp 9Môn Sinh học Lớp 9SGK Sinh lớp 9 SBT Sinh lớp 9 Vở bài tập Sinh học 9 Đề thi, đề kiểm tra Sinh lớp 9 Bài tập trắc nghiệm Sinh 9 Đề thi, đề kiểm tra Sinh lớp 9Môn Lịch sử Lớp 9SGK Lịch sử lớp 9 VBT Lịch sử lớp 9 Tập bản đồ Lịch sử lớp 9 SBT Lịch sử lớp 9 Đề thi, kiểm tra Lịch sử lớp 9Môn Địa lí Lớp 9Đề thi, kiểm tra Địa lí lớp 9 SGK Địa lí lớp 9 SBT Địa lí lớp 9 VBT Địa lí lớp 9 Tập bản đồ Địa lí lớp 9Môn Công nghệ Lớp 9SGK Công nghệ 9Môn Tin học Lớp 9SGK Tin học lớp 9Môn Khoa học tự nhiên Lớp 9SGK Khoa học tự nhiên – Cánh diều SGK Khoa học tự nhiên – Chân trời sáng tạo SGK Khoa học tự nhiên – Kết nối tri thứcMôn Âm nhạc và mỹ thuật Lớp 9Âm nhạc và mỹ thuật lớp 9 HỌC NGAY
Môn Toán học Lớp 8Bài tập trắc nghiệm Toán – Cánh diều SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SGK Toán 8 – Cùng khám phá SBT Toán – Kết nối tri thức SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Vở thực hành Toán Xem thêmMôn Ngữ văn Lớp 8Bài tập trắc nghiệm Văn – Chân trời sáng tạo Văn mẫu – Kết nối tri thức Soạn văn chi tiết – KNTT Văn mẫu – Chân trời sáng tạo Soạn văn siêu ngắn – KNTT Văn mẫu – Cánh Diều Soạn văn chi tiết – CTST Đề thi, đề kiểm tra Văn – Kết nối tri thức Soạn văn siêu ngắn – CTST Xem thêmMôn Tiếng Anh Lớp 8Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Đề thi, đề kiểm tra Tiếng Anh 8 mới Lý thuyết Tiếng Anh 8 Tiếng Anh – Global Success Tiếng Anh – Friends Plus Tiếng Anh – iLearn Smart World Xem thêmMôn GDCD Lớp 8Giáo dục công dân – Kết nối tri thức Giáo dục công dân – Chân trời sáng tạo Giáo dục công dân – Cánh diềuMôn Công nghệ Lớp 8SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 8SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 8SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diều SGK Giáo dục thể chất – Chân trời sáng tạoMôn Khoa học tự nhiên Lớp 8SGK Khoa học tự nhiên – Kết nối tri thức SGK Khoa học tự nhiên – Cánh diều SBT KHTN – Kết nối tri thức SBT KHTN – Cánh diều Vở thực hành Khoa học tự nhiên Đề thi, đề kiểm tra KHTN – Kết nối tri thức Đề thi, đề kiểm tra KHTN – Cánh diều Lý thuyết Khoa học tự nhiên 8 Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Xem thêmMôn Lịch sử và Địa lí Lớp 8SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Cánh diều SGK Lịch sử và Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Lịch Sử và Địa lí – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Lịch Sử và Địa lí – Cánh diều
HỌC NGAY
Môn Toán học Lớp 8Bài tập trắc nghiệm Toán – Cánh diều SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SGK Toán 8 – Cùng khám phá SBT Toán – Kết nối tri thức SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Vở thực hành Toán Xem thêmMôn Ngữ văn Lớp 8Bài tập trắc nghiệm Văn – Chân trời sáng tạo Văn mẫu – Kết nối tri thức Soạn văn chi tiết – KNTT Văn mẫu – Chân trời sáng tạo Soạn văn siêu ngắn – KNTT Văn mẫu – Cánh Diều Soạn văn chi tiết – CTST Đề thi, đề kiểm tra Văn – Kết nối tri thức Soạn văn siêu ngắn – CTST Xem thêmMôn Tiếng Anh Lớp 8Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Đề thi, đề kiểm tra Tiếng Anh 8 mới Lý thuyết Tiếng Anh 8 Tiếng Anh – Global Success Tiếng Anh – Friends Plus Tiếng Anh – iLearn Smart World Xem thêmMôn GDCD Lớp 8Giáo dục công dân – Kết nối tri thức Giáo dục công dân – Chân trời sáng tạo Giáo dục công dân – Cánh diềuMôn Công nghệ Lớp 8SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 8SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 8SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diều SGK Giáo dục thể chất – Chân trời sáng tạoMôn Khoa học tự nhiên Lớp 8SGK Khoa học tự nhiên – Kết nối tri thức SGK Khoa học tự nhiên – Cánh diều SBT KHTN – Kết nối tri thức SBT KHTN – Cánh diều Vở thực hành Khoa học tự nhiên Đề thi, đề kiểm tra KHTN – Kết nối tri thức Đề thi, đề kiểm tra KHTN – Cánh diều Lý thuyết Khoa học tự nhiên 8 Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Xem thêmMôn Lịch sử và Địa lí Lớp 8SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Cánh diều SGK Lịch sử và Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Lịch Sử và Địa lí – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí – Chân trời sáng tạo Đề thi, kiểm tra Lịch Sử và Địa lí – Cánh diều HỌC NGAY
Môn Toán học Lớp 7Vở thực hành SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SBT Toán – Kết nối tri thức SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Xem thêmMôn Ngữ văn Lớp 7Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Cánh diều Bài tập trắc nghiệm Văn – Kết nối tri thức Bài tập trắc nghiệm Văn – Chân trời sáng tạo Bài tập trắc nghiệm Văn – Cánh diều Vở thực hành văn Lý thuyết Văn 7 SBT Văn – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Kết nối tri thức Xem thêmMôn Tiếng Anh Lớp 7Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Lý thuyết Tiếng Anh 7 Bài tập trắc nghiệm Tiếng Anh – Friends Plus Bài tập trắc nghiệm Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Global Success Tiếng Anh – Global Success Xem thêmMôn Công nghệ Lớp 7SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn Tin học Lớp 7SGK Tin học – Kết nối tri thức SGK Tin học – Cánh Diều SGK Tin học – Chân trời sáng tạo SBT Tin học – Kết nối tri thứcMôn HĐ trải nghiệm, hướng nghiệp Lớp 7SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh Diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạoMôn Khoa học tự nhiên Lớp 7SGK Khoa học tự nhiên – Kết nối tri thức SGK Khoa học tự nhiên – Chân trời sáng tạo SGK Khoa học tự nhiên – Cánh diều SBT KHTN – Kết nối tri thức SBT KHTN – Chân trời sáng tạo SBT KHTN – Cánh diều Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Bài tập trắc nghiệm Khoa học tự nhiên – Chân trời sáng tạo Bài tập trắc nghiệm Khoa học tự nhiên – Cánh diều Xem thêmMôn Lịch sử và Địa lí Lớp 7SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Chân trời sáng tạo SGK Lịch sử và Địa lí – Cánh Diều SBT Lịch sử và Địa lí – Kết nối tri thức SBT Lịch sử và Địa lí – Chân trời sáng tạo SBT Lịch sử và Địa lí – Cánh diều Đề thi, kiểm tra Lịch sử và Địa lí lớp 7 – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí lớp 7 – Chân trời sáng tạo
HỌC NGAY
Môn Toán học Lớp 7Vở thực hành SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SBT Toán – Kết nối tri thức SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Xem thêmMôn Ngữ văn Lớp 7Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Cánh diều Bài tập trắc nghiệm Văn – Kết nối tri thức Bài tập trắc nghiệm Văn – Chân trời sáng tạo Bài tập trắc nghiệm Văn – Cánh diều Vở thực hành văn Lý thuyết Văn 7 SBT Văn – Chân trời sáng tạo Đề thi, đề kiểm tra Văn – Kết nối tri thức Xem thêmMôn Tiếng Anh Lớp 7Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Lý thuyết Tiếng Anh 7 Bài tập trắc nghiệm Tiếng Anh – Friends Plus Bài tập trắc nghiệm Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Global Success Tiếng Anh – Global Success Xem thêmMôn Công nghệ Lớp 7SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn Tin học Lớp 7SGK Tin học – Kết nối tri thức SGK Tin học – Cánh Diều SGK Tin học – Chân trời sáng tạo SBT Tin học – Kết nối tri thứcMôn HĐ trải nghiệm, hướng nghiệp Lớp 7SGK Hoạt động trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Hoạt động trải nghiệm, hướng nghiệp – Cánh Diều SGK Hoạt động trải nghiệm, hướng nghiệp – Chân trời sáng tạoMôn Khoa học tự nhiên Lớp 7SGK Khoa học tự nhiên – Kết nối tri thức SGK Khoa học tự nhiên – Chân trời sáng tạo SGK Khoa học tự nhiên – Cánh diều SBT KHTN – Kết nối tri thức SBT KHTN – Chân trời sáng tạo SBT KHTN – Cánh diều Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Bài tập trắc nghiệm Khoa học tự nhiên – Chân trời sáng tạo Bài tập trắc nghiệm Khoa học tự nhiên – Cánh diều Xem thêmMôn Lịch sử và Địa lí Lớp 7SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Chân trời sáng tạo SGK Lịch sử và Địa lí – Cánh Diều SBT Lịch sử và Địa lí – Kết nối tri thức SBT Lịch sử và Địa lí – Chân trời sáng tạo SBT Lịch sử và Địa lí – Cánh diều Đề thi, kiểm tra Lịch sử và Địa lí lớp 7 – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí lớp 7 – Chân trời sáng tạo HỌC NGAY
Môn Toán học Lớp 6Vở thực hành Toán 6 SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SBT Toán – Kết nối tri thức SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Xem thêmMôn Ngữ văn Lớp 6Vở thực hành văn Ôn tập hè Văn lớp 6 Đề thi, đề kiểm tra Văn – Cánh diều Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Soạn văn siêu ngắn – KNTT Văn mẫu 6- Kết nối tri thức Soạn văn chi tiết – KNTT Văn mẫu 6 – Cánh diều Soạn văn siêu ngắn – CTST Xem thêmMôn Tiếng Anh Lớp 6Bài tập trắc nghiệm Tiếng Anh 6 – English Discovery Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Ôn tập hè Tiếng Anh lớp 6 Bài tập trắc nghiệm Tiếng Anh – Right on! Global Success (Pearson) Xem thêmMôn GDCD Lớp 6SGK GDCD – CTST SGK GDCD – Cánh Diều SBT GDCD – Kết nối tri thức SBT GDCD – Chân trời sáng tạo SBT GDCD – Cánh diều SGK GDCD – KNTTMôn Công nghệ Lớp 6Công nghệ – Kết nối tri thức Công nghệ – Cánh Diều Công nghệ – Chân trời sáng tạo SBT Công nghệ – Kết nối tri thức SBT Công nghệ – Cánh diều SBT Công nghệ – Chân trời sáng tạoMôn Tin học Lớp 6Tin học – Kết nối tri thức + chân trời sáng tạo Tin học – Cánh Diều SBT Tin học – Kết nối tri thức SBT Tin học – Cánh DiềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 6SGK Trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Trải nghiệm, hướng nghiệp – Chân trời sáng tạo SGK Trải nghiệm, hướng nghiệp – Cánh diều SBT Trải nghiệm, hướng nghiệp – Kết nối tri thức SBT Trải nghiệm, hướng nghiệp – Chân trời sáng tạo Thực hành Trải nghiệm, hướng nghiệp – Cánh diềuMôn Khoa học tự nhiên Lớp 6SGK KHTN – Kết nối tri thức SGK KHTN – Chân trời sáng tạo SGK KHTN – Cánh Diều SBT KHTN – Kết nối tri thức SBT KHTN – Chân trời sáng tạo SBT KHTN – Cánh Diều Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Bài tập trắc nghiệm Khoa học tự nhiên – Chân trời sáng tạo Bài tập trắc nghiệm Khoa học tự nhiên – Cánh diều Xem thêmMôn Lịch sử và Địa lí Lớp 6SGK Lịch sử và Địa lí – KNTT SGK Lịch sử và Địa lí – CTST SGK Lịch sử và Địa lí – Cánh Diều SBT Lịch sử và Địa lí – KNTT SBT Lịch sử và Địa lí – CTST SBT Lịch sử và Địa lí – Cánh diều Đề thi, kiểm tra Lịch sử và Địa lí – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí – Cánh Diều Đề thi, kiểm tra Lịch sử và Địa lí – Chân trời sáng tạoMôn Mỹ thuật Lớp 6Mĩ thuật – Kết nối tri thức Mĩ thuật – Chân trời sáng tạo Mĩ thuật – Cánh diều
HỌC NGAY
Môn Toán học Lớp 6Vở thực hành Toán 6 SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh diều SBT Toán – Kết nối tri thức SBT Toán – Chân trời sáng tạo SBT Toán – Cánh diều Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Xem thêmMôn Ngữ văn Lớp 6Vở thực hành văn Ôn tập hè Văn lớp 6 Đề thi, đề kiểm tra Văn – Cánh diều Đề thi, đề kiểm tra Văn – Chân trời sáng tạo Soạn văn siêu ngắn – KNTT Văn mẫu 6- Kết nối tri thức Soạn văn chi tiết – KNTT Văn mẫu 6 – Cánh diều Soạn văn siêu ngắn – CTST Xem thêmMôn Tiếng Anh Lớp 6Bài tập trắc nghiệm Tiếng Anh 6 – English Discovery Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Friends Plus Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart World Đề thi, đề kiểm tra Tiếng Anh – Right on! Đề thi, đề kiểm tra Tiếng Anh – English Discovery Ôn tập hè Tiếng Anh lớp 6 Bài tập trắc nghiệm Tiếng Anh – Right on! Global Success (Pearson) Xem thêmMôn GDCD Lớp 6SGK GDCD – CTST SGK GDCD – Cánh Diều SBT GDCD – Kết nối tri thức SBT GDCD – Chân trời sáng tạo SBT GDCD – Cánh diều SGK GDCD – KNTTMôn Công nghệ Lớp 6Công nghệ – Kết nối tri thức Công nghệ – Cánh Diều Công nghệ – Chân trời sáng tạo SBT Công nghệ – Kết nối tri thức SBT Công nghệ – Cánh diều SBT Công nghệ – Chân trời sáng tạoMôn Tin học Lớp 6Tin học – Kết nối tri thức + chân trời sáng tạo Tin học – Cánh Diều SBT Tin học – Kết nối tri thức SBT Tin học – Cánh DiềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 6SGK Trải nghiệm, hướng nghiệp – Kết nối tri thức SGK Trải nghiệm, hướng nghiệp – Chân trời sáng tạo SGK Trải nghiệm, hướng nghiệp – Cánh diều SBT Trải nghiệm, hướng nghiệp – Kết nối tri thức SBT Trải nghiệm, hướng nghiệp – Chân trời sáng tạo Thực hành Trải nghiệm, hướng nghiệp – Cánh diềuMôn Khoa học tự nhiên Lớp 6SGK KHTN – Kết nối tri thức SGK KHTN – Chân trời sáng tạo SGK KHTN – Cánh Diều SBT KHTN – Kết nối tri thức SBT KHTN – Chân trời sáng tạo SBT KHTN – Cánh Diều Bài tập trắc nghiệm Khoa học tự nhiên – Kết nối tri thức Bài tập trắc nghiệm Khoa học tự nhiên – Chân trời sáng tạo Bài tập trắc nghiệm Khoa học tự nhiên – Cánh diều Xem thêmMôn Lịch sử và Địa lí Lớp 6SGK Lịch sử và Địa lí – KNTT SGK Lịch sử và Địa lí – CTST SGK Lịch sử và Địa lí – Cánh Diều SBT Lịch sử và Địa lí – KNTT SBT Lịch sử và Địa lí – CTST SBT Lịch sử và Địa lí – Cánh diều Đề thi, kiểm tra Lịch sử và Địa lí – Kết nối tri thức Đề thi, kiểm tra Lịch sử và Địa lí – Cánh Diều Đề thi, kiểm tra Lịch sử và Địa lí – Chân trời sáng tạoMôn Mỹ thuật Lớp 6Mĩ thuật – Kết nối tri thức Mĩ thuật – Chân trời sáng tạo Mĩ thuật – Cánh diều HỌC NGAY
Môn Toán học Lớp 5SGK Toán 5 – Bình Minh SGK Toán lớp 5 VNEN Toán lớp 5 Vở bài tập Toán 5 Bài tập cuối tuần Toán 5 Cùng em học toán lớp 5 Bài tập trắc nghiệm Toán 5 Đề thi, đề kiểm tra Toán lớp 5 Bài tập phát triển năng lực Toán lớp 5 Xem thêmMôn Tiếng Anh Lớp 5SGK Tiếng Anh lớp 5 Mới Đề thi vào lớp 6 môn Tiếng Anh Chứng chỉ Cambridge Pre A1 Starters SBT Tiếng Anh lớp 5 Đề thi, đề kiểm tra Tiếng Anh lớp 5 Tiếng Anh – Global Success Tiếng Anh – Family and Friends Tiếng Anh – iLearn Smart Start Tiếng Anh – Explore Our WorldMôn Lịch sử và Địa lí Lớp 5SGK Lịch sử và Địa lí lớp 5 Vở bài tập Lịch sử lớp 5 Vở bài tập Địa lí lớp 5
HỌC NGAY
Môn Toán học Lớp 5SGK Toán 5 – Bình Minh SGK Toán lớp 5 VNEN Toán lớp 5 Vở bài tập Toán 5 Bài tập cuối tuần Toán 5 Cùng em học toán lớp 5 Bài tập trắc nghiệm Toán 5 Đề thi, đề kiểm tra Toán lớp 5 Bài tập phát triển năng lực Toán lớp 5 Xem thêmMôn Tiếng Anh Lớp 5SGK Tiếng Anh lớp 5 Mới Đề thi vào lớp 6 môn Tiếng Anh Chứng chỉ Cambridge Pre A1 Starters SBT Tiếng Anh lớp 5 Đề thi, đề kiểm tra Tiếng Anh lớp 5 Tiếng Anh – Global Success Tiếng Anh – Family and Friends Tiếng Anh – iLearn Smart Start Tiếng Anh – Explore Our WorldMôn Lịch sử và Địa lí Lớp 5SGK Lịch sử và Địa lí lớp 5 Vở bài tập Lịch sử lớp 5 Vở bài tập Địa lí lớp 5 HỌC NGAY
Môn Toán học Lớp 4Toán nâng cao lớp 4 Bài tập trắc nghiệm Toán – Kết nối tri thức SGK Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Cánh diều SGK Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Chân trời sáng tạo SGK Toán – Cánh diều SGK Toán 4 – Bình Minh VBT Toán – Kết nối tri thức Xem thêmMôn Tiếng Anh Lớp 4Đề thi, đề kiểm tra Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart Start Tiếng Anh – Global Sucess Đề thi, đề kiểm tra Tiếng Anh – Phonics Smart Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh – Explore Our World Tiếng Anh – iLearn Smart Start Chứng chỉ Cambridge Pre A1 Starters Tiếng Anh – Phonics Smart Xem thêmMôn Công nghệ Lớp 4SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 4SGK Hoạt động trải nghiệm – Kết nối tri thức SGK Hoạt động trải nghiệm – Cánh diều SGK Hoạt động trải nghiệm – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 4SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diều SGK Giáo dục thể chất – Chân trời sáng tạoMôn Lịch sử và Địa lí Lớp 4SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Chân trời sáng tạo SGK Lịch sử và Địa lí – Cánh diềuMôn Âm nhạc Lớp 4SGK Âm nhạc – Kết nối tri thức SGK Âm nhạc – Chân trời sáng tạo SGK Âm nhạc – Cánh diềuMôn Mỹ thuật Lớp 4SGK Mĩ thuật – Kết nối tri thức SGK Mĩ thuật – Cánh diều SGK Mĩ thuật – Chân trời sáng tạo bản 1 SGK Mĩ thuật – Chân trời sáng tạo bản 2Môn Tiếng việt Lớp 4Đề thi, đề kiểm tra Tiếng Việt – Kết nối tri thức Đề thi, đề kiểm tra Tiếng Việt – Chân trời sáng tạo Đề thi, đề kiểm tra Tiếng Việt – Cánh diều Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh diều VBT Tiếng Việt – Kết nối tri thức SGK Tiếng Việt 4 Cùng em học Tiếng Việt 4 Xem thêm
HỌC NGAY
Môn Toán học Lớp 4Toán nâng cao lớp 4 Bài tập trắc nghiệm Toán – Kết nối tri thức SGK Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Cánh diều SGK Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Chân trời sáng tạo SGK Toán – Cánh diều SGK Toán 4 – Bình Minh VBT Toán – Kết nối tri thức Xem thêmMôn Tiếng Anh Lớp 4Đề thi, đề kiểm tra Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart Start Tiếng Anh – Global Sucess Đề thi, đề kiểm tra Tiếng Anh – Phonics Smart Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh – Explore Our World Tiếng Anh – iLearn Smart Start Chứng chỉ Cambridge Pre A1 Starters Tiếng Anh – Phonics Smart Xem thêmMôn Công nghệ Lớp 4SGK Công nghệ – Kết nối tri thức SGK Công nghệ – Chân trời sáng tạo SGK Công nghệ – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 4SGK Hoạt động trải nghiệm – Kết nối tri thức SGK Hoạt động trải nghiệm – Cánh diều SGK Hoạt động trải nghiệm – Chân trời sáng tạo Bản 1 SGK Hoạt động trải nghiệm – Chân trời sáng tạo Bản 2Môn Giáo dục thể chất Lớp 4SGK Giáo dục thể chất – Kết nối tri thức SGK Giáo dục thể chất – Cánh diều SGK Giáo dục thể chất – Chân trời sáng tạoMôn Lịch sử và Địa lí Lớp 4SGK Lịch sử và Địa lí – Kết nối tri thức SGK Lịch sử và Địa lí – Chân trời sáng tạo SGK Lịch sử và Địa lí – Cánh diềuMôn Âm nhạc Lớp 4SGK Âm nhạc – Kết nối tri thức SGK Âm nhạc – Chân trời sáng tạo SGK Âm nhạc – Cánh diềuMôn Mỹ thuật Lớp 4SGK Mĩ thuật – Kết nối tri thức SGK Mĩ thuật – Cánh diều SGK Mĩ thuật – Chân trời sáng tạo bản 1 SGK Mĩ thuật – Chân trời sáng tạo bản 2Môn Tiếng việt Lớp 4Đề thi, đề kiểm tra Tiếng Việt – Kết nối tri thức Đề thi, đề kiểm tra Tiếng Việt – Chân trời sáng tạo Đề thi, đề kiểm tra Tiếng Việt – Cánh diều Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh diều VBT Tiếng Việt – Kết nối tri thức SGK Tiếng Việt 4 Cùng em học Tiếng Việt 4 Xem thêm HỌC NGAY
Môn Toán học Lớp 3Ôn tập hè Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Kết nối tri thức Bài tập cuối tuần môn Toán 3 Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Cùng em học Toán 3 Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Xem thêmMôn Tiếng Anh Lớp 3Đề thi, đề kiểm tra Tiếng Anh – Explore Our World Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart Start Đề thi, đề kiểm tra Tiếng Anh – Phonics Smart Chứng chỉ Cambridge Pre A1 Starters Bài tập trắc nghiệm Tiếng Anh – iLearn Smart Start Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Family and Friends Tiếng Anh – Global Success Tiếng Anh – Family and Friends Xem thêmMôn Tin học Lớp 3SGK Tin học – Kết nối tri thức SGK Tin học – Chân trời sáng tạo SGK Tin học – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 3SGK Hoạt động trải nghiệm- Kết nối tri thức SGK Hoạt động trải nghiệm- Chân trời sáng tạo SGK Hoạt động trải nghiệm – Cánh diềuMôn Tiếng việt Lớp 3Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh diều VBT Tiếng Việt – Kết nối tri thức VBT Tiếng Việt – Chân trời sáng tạo VBT Tiếng Việt – Cánh diều Văn mẫu – Kết nối tri thức Cùng em học Tiếng Việt 3 Văn mẫu lớp 3Môn Tự nhiên và xã hội Lớp 3Tự nhiên và xã hội – Kết nối tri thức Tự nhiên và xã hội – Chân trời sáng tạo Tự nhiên và xã hội – Cánh diều
HỌC NGAY
Môn Toán học Lớp 3Ôn tập hè Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Kết nối tri thức Bài tập cuối tuần môn Toán 3 Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Cùng em học Toán 3 Bài tập trắc nghiệm Toán – Kết nối tri thức Bài tập trắc nghiệm Toán – Chân trời sáng tạo Bài tập trắc nghiệm Toán – Cánh diều Xem thêmMôn Tiếng Anh Lớp 3Đề thi, đề kiểm tra Tiếng Anh – Explore Our World Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart Start Đề thi, đề kiểm tra Tiếng Anh – Phonics Smart Chứng chỉ Cambridge Pre A1 Starters Bài tập trắc nghiệm Tiếng Anh – iLearn Smart Start Đề thi, đề kiểm tra Tiếng Anh – Global Success Đề thi, đề kiểm tra Tiếng Anh – Family and Friends Tiếng Anh – Global Success Tiếng Anh – Family and Friends Xem thêmMôn Tin học Lớp 3SGK Tin học – Kết nối tri thức SGK Tin học – Chân trời sáng tạo SGK Tin học – Cánh diềuMôn HĐ trải nghiệm, hướng nghiệp Lớp 3SGK Hoạt động trải nghiệm- Kết nối tri thức SGK Hoạt động trải nghiệm- Chân trời sáng tạo SGK Hoạt động trải nghiệm – Cánh diềuMôn Tiếng việt Lớp 3Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh diều VBT Tiếng Việt – Kết nối tri thức VBT Tiếng Việt – Chân trời sáng tạo VBT Tiếng Việt – Cánh diều Văn mẫu – Kết nối tri thức Cùng em học Tiếng Việt 3 Văn mẫu lớp 3Môn Tự nhiên và xã hội Lớp 3Tự nhiên và xã hội – Kết nối tri thức Tự nhiên và xã hội – Chân trời sáng tạo Tự nhiên và xã hội – Cánh diều HỌC NGAY
Môn Toán học Lớp 2SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh Diều VBT Toán – KNTT VBT Toán – CTST Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Cùng em học Toán 2 Xem thêmMôn Tiếng Anh Lớp 2Đề thi, đề kiểm tra Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart Start Đề thi, đề kiểm tra Tiếng Anh – Phonics Smart Đề thi, đề kiểm tra Tiếng Anh – English Discovery Chứng chỉ Cambridge Pre A1 Starters SBT Kết nối tri thức SBT Family and Friends SBT iLearn Smart Start SBT Phonics Smart Xem thêmMôn HĐ trải nghiệm, hướng nghiệp Lớp 2VBT Hoạt động trải nghiệm – Chân trời sáng tạo VTH Hoạt động trải nghiệm – Cánh Diều VBT Hoạt động trải nghiệm – Kết nối tri thứcMôn Âm nhạc Lớp 2Âm nhạc 2 – Kết nối tri thức Âm nhạc 2 – Chân trời sáng tạo Âm nhạc 2 – Cánh diều VBT Âm nhạc – Kết nối tri thức VBT Âm nhạc – Chân trời sáng tạo VBT Âm nhạc – Cánh diềuMôn Tiếng việt Lớp 2Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh Diều Văn mẫu – Kết nối tri thức Văn mẫu – Chân trời sáng tạo Văn mẫu – Cánh diều VBT Tiếng Việt – Kết nối tri thức VBT Tiếng Việt – Chân trời sáng tạo VBT Tiếng Việt – Cánh diều Xem thêm
HỌC NGAY
Môn Toán học Lớp 2SGK Toán – Kết nối tri thức SGK Toán – Chân trời sáng tạo SGK Toán – Cánh Diều VBT Toán – KNTT VBT Toán – CTST Đề thi, đề kiểm tra Toán – Kết nối tri thức Đề thi, đề kiểm tra Toán – Chân trời sáng tạo Đề thi, đề kiểm tra Toán – Cánh diều Cùng em học Toán 2 Xem thêmMôn Tiếng Anh Lớp 2Đề thi, đề kiểm tra Tiếng Anh – Family and Friends Đề thi, đề kiểm tra Tiếng Anh – iLearn Smart Start Đề thi, đề kiểm tra Tiếng Anh – Phonics Smart Đề thi, đề kiểm tra Tiếng Anh – English Discovery Chứng chỉ Cambridge Pre A1 Starters SBT Kết nối tri thức SBT Family and Friends SBT iLearn Smart Start SBT Phonics Smart Xem thêmMôn HĐ trải nghiệm, hướng nghiệp Lớp 2VBT Hoạt động trải nghiệm – Chân trời sáng tạo VTH Hoạt động trải nghiệm – Cánh Diều VBT Hoạt động trải nghiệm – Kết nối tri thứcMôn Âm nhạc Lớp 2Âm nhạc 2 – Kết nối tri thức Âm nhạc 2 – Chân trời sáng tạo Âm nhạc 2 – Cánh diều VBT Âm nhạc – Kết nối tri thức VBT Âm nhạc – Chân trời sáng tạo VBT Âm nhạc – Cánh diềuMôn Tiếng việt Lớp 2Tiếng Việt – Kết nối tri thức Tiếng Việt – Chân trời sáng tạo Tiếng Việt – Cánh Diều Văn mẫu – Kết nối tri thức Văn mẫu – Chân trời sáng tạo Văn mẫu – Cánh diều VBT Tiếng Việt – Kết nối tri thức VBT Tiếng Việt – Chân trời sáng tạo VBT Tiếng Việt – Cánh diều Xem thêm HỌC NGAY
Môn Tiếng Anh Lớp 1Chứng chỉ Cambridge Pre A1 StartersMôn Tiếng việt Lớp 1Đề thi, đề kiểm tra Tiếng Việt 1 SGK Tiếng Việt – Kết nối tri thức SGK Tiếng Việt – Chân trời sáng tạo SGK Tiếng Việt – Cánh diềuMôn Đạo đức Lớp 1VBT Đạo Đức 1
HỌC NGAY
Môn Tiếng Anh Lớp 1Chứng chỉ Cambridge Pre A1 StartersMôn Tiếng việt Lớp 1Đề thi, đề kiểm tra Tiếng Việt 1 SGK Tiếng Việt – Kết nối tri thức SGK Tiếng Việt – Chân trời sáng tạo SGK Tiếng Việt – Cánh diềuMôn Đạo đức Lớp 1VBT Đạo Đức 1








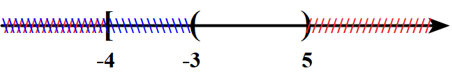
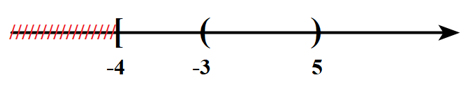
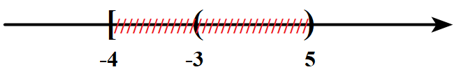










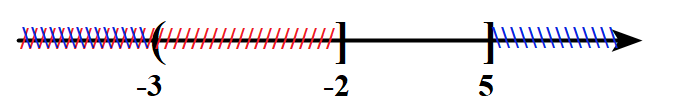




 B.
B.  C.
C.  D.
D.