1. Đề cương ôn tập học kì 1

A. NỘI DUNG ÔN TẬP

Số học

1. Số tự nhiên

– Tập hợp

– Phép cộng, trừ, nhân, chia số tự nhiên

– Lũy thừa với số mũ tự nhiên

2. Tính chia hết

– Tính chất chia hết

– Dấu hiệu chia hết

– Số nguyên tố

– Ước chung. Ước chung lớn nhất

– Bội chung. Bội chung nhỏ nhất

3. Số nguyên

– Tập hợp số nguyên

– Phép cộng, trừ, nhân số nguyên

– Phép chia hết. Ước và bội của số nguyên

Hình học

1. Hình phẳng

– Tam giác đều, hình vuông, hình lục giác đều

– Hình chữ nhật, hình thoi, hình bình hành, hình thang cân

– Chu vi và diện tích tứ giác

2. Tính đối xứng

– Hình có trục đối xứng

– Hình có tâm đối xứng

B. BÀI TẬP

Đề bài

I. Phần trắc nghiệm

Câu 1: Cho tập A là tập hợp các số tự nhiên nhỏ hơn hoặc bằng 10. Cách viết nào dưới đây biểu diễn đúng tập A?

A. \(A = \left\{ {0;1;2;3;4;5;6;7;8} \right\}\).

B. \(A = \left\{ {0;1;2;3;4;5;6;7;8;9;10} \right\}\).

C. \(A = \left\{ {n \in \mathbb{N}|n < 10} \right\}\).

D. \(A = \left\{ {n \in \mathbb{Q}*|n \le 10} \right\}\).

Câu 2: Kết quả của phép tính \({5^7}.18 – {5^7}.13\) là:

A. \(5\).

B. \({5^8}\).

C. \({5^7}\).

D. \({5^6}\).

Câu 3: Kết quả dãy tính 200 – 199 + 198 – 197 + … + 4 – 3 + 2 – 1 bằng

A. 199.

B. 101.

C. 100.

D. 5050.

Câu 4: Nếu \(a = b.k\left( {b \ne 0} \right)\). Khẳng định nào dưới đây là sai ?

A. a chia hết cho b.

B. a là ước của b.

C. a là bội của b.

D. b là ước của a.

Câu 5: Nếu \(a \vdots 5\) và \(b \vdots 5\) \(\left( {a > b} \right)\) thì

A. \(\left( {a + b} \right) \vdots 5\).

B. \(\left( {a – b} \right) \vdots 5\).

C. \(\left( {2a – b} \right) \vdots 5\).

D. Tất cả đều đúng.

Câu 6: Nếu M = 12a + 14b thì

A. \(M \vdots 12\).

B. \(M \vdots 14\).

C. \(M \vdots 2\).

D. \(M \vdots 7\).

Câu 7: Thay chữ số vào dấu * để được \(\overline {1*} \) là số nguyên tố

A. 1; 2; 3; 7; 9.

B. 1; 3; 5; 7; 9.

C. 1; 3; 7; 9.

D. 1; 2; 5.

Câu 8: Trong các câu sau, chọn câu đúng nhất:

A. Mọi số nguyên tố đều là số lẻ.

B. Các số tự nhiên nếu không là số nguyên tố thì chỉ có thể là hợp số.

C. Có hai số tự nhiên liên tiếp đều là số nguyên tố.

D. Hợp số là số tự nhiên chỉ có 3 ước.

Câu 9: Số \({10^4} + 2\) chia hết cho số nào dưới đây?

A. 3; 9.

B. 2; 5.

C. 2; 3.

D. 3; 5.

Câu 10: Số tự nhiên a lớn nhất thỏa mãn \(90 \vdots a\) và \(135 \vdots a\) là:

A. 15.

B. 30.

C. 45.

D. 60.

Câu 11: Tìm số tự nhiên a biết 398 chia cho a dư 38, còn 450 chia cho a dư 18.

A. 2.

B. 72.

C. 89550.

D. 342.

Câu 12: Khẳng định nào sau đây là sai:

A. Các số nguyên dương luôn lớn hơn 0 .

B. Các số nguyên âm luôn nhỏ hơn các số nguyên dương.

C. Các số nguyên âm luôn lớn hơn 0 và nhỏ hơn các số nguyên dương.

D. Số 0 luôn lớn hơn các số nguyên âm và nhỏ hơn các số nguyên dương.

Câu 13: “Trên trục số, điểm cách 0 mười đơn vị biểu diễn các số nguyên nào?

A. 0 và 10.

B. -10.

C. 10.

D. 10 và -10.

Câu 14: Dãy số nào dưới đây được viết theo thứ tự giảm dần?

A. 28; 19; 0; -36; -21.

B. -49; -40; -35; -20; 0.

C. -5; -16; 18; 21; 30.

D. 21; 19; 0; -11; -15.

Câu 15: Tập hợp các số nguyên x thỏa mãn \( – 2 \le x < 3\) là:

A. {0; 1; 2; 3}.

B. {-1; 0; 1; 2}.

C. {-2; -1; 0; 1; 2}.

D. {-2; -1; 0; 1; 2; 3}.

Câu 16: Tổng các số nguyên x thỏa mãn \( – 100 < x \le 100\) là:

A. 99.

B. -100.

C. 0.

D. 100.

Câu 17: Kết quả phép tính (23 + 1478) – (1478 – 77) là:

A. -2856.

B. 3056.

C. 100.

D. -54.

Câu 18: Cho a là số nguyên âm lớn nhất có ba chữ số, b là số nguyên âm nhỏ nhất có hai chữ số. Kết quả phép tính a – b là

A. 199.

B. -199.

C. 1.

D. -1.

Câu 19: Khi bỏ dấu ngoặc trong biểu thức 2009 – (5 – 9 + 2008) ta được:

A. 2009 + 5 – 9 – 2008.

B. 2009 + 5 – 9 + 2008.

C. 2009 – 5 + 9 – 2008.

D. 2009 – 5 + 9 + 2008.

Câu 20: Giá trị x thỏa mãn biểu thức 2x – 1 = 3 – (-x + 5) là

A. 0.

B. -2.

C. -1.

D. 1.

Câu 21: Giá trị của biểu thức -15 – 17 + 12 – (12 – 15) bằng

A. -12.

B. -15.

C. -17.

D. -18.

Câu 22: Nếu x, y > 0 thì

A. x, y cùng dấu.

B. x > y.

C. x, y khác dấu.

D. x < y.

Câu 23: Độ dài cạnh còn lại của hình bình hành có chu vi 24cm và một cạnh dài 5cm là

A. 7cm.

B. 19cm.

C. 17cm.

D. 43cm.

Câu 24: Trong các hình dưới đây, hình nào có diện tích bé nhất?

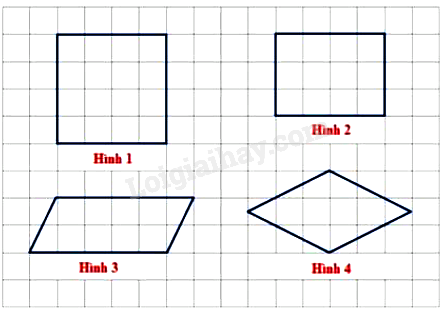
A. Hình 1.

B. Hình 2.

C. Hình 3.

D. Hình 4.

Câu 25. Khẳng định nào sau đây sai?

A. Hai đường chéo của hình vuông bằng nhau.

B. Hai đường chéo của hình bình hành bằng nhau.

C. Hai đường chéo của hình thoi vuông góc.

D. Hai cạnh bên của hình thang cân bằng nhau.

Câu 26: Diện tích phần tô màu trong hình dưới đây là bao nhiêu?

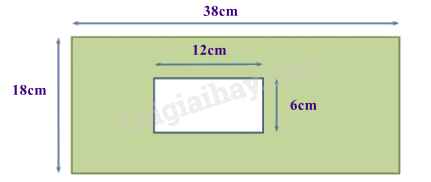
A. \(612\left( {c{m^2}} \right)\).

B. \(612\left( {cm} \right)\).

C. \(648\left( {c{m^2}} \right)\).

D. \(648\left( {cm} \right)\).

Câu 27: Cần bao nhiêu viên gạch hình vuông cạnh 45cm để lát nền nhà hình chữ nhật có chiều dài 27m, chiều rộng 9m?

A. 1200 viên.

B. 1100 viên.

C. 1000 viên.

D. 900 viên.

Câu 28: Trong các biển báo giao thông sau, biển báo nào không có trục đối xứng?

A. Biển báo cấm đi ngược chiều (hình a).

B. Biển báo cấm dừng xe và đỗ xe (hình b).

C. Biển báo cấm sử dụng còi (hình c).

D. Biển báo đường cấm (hình d).

Câu 29: Những hình nào sau đây có tâm đối xứng?

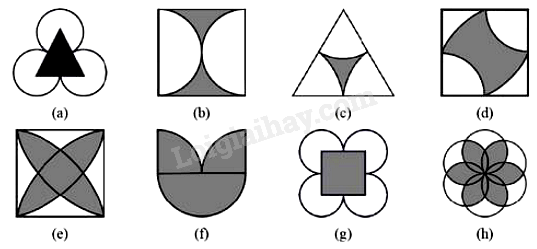
A. Hình (b), (d), (e), (g), (h).

B. Hình (a), (b), (c), (e), (g), (h).

C. Hình (a), (e), (g), (h).

D. Hình (b), (c), (e), (g).

Câu 30: Cho các hình sau đây:

(1) Đoạn thẳng AB

(2) Tam giác đều ABC

(3) Hình tròn tâm O

Trong các hình trên, các hình có tâm đối xứng là:

A. (1).

B. (1), (2).

C. (1), (3).

D. (1), (2), (3).

II. Phần tự luận

Bài 1. Thực hiện phép tính:

a) \(425 + 378 – 125 + 122\).

b) \(\left( {{2^3}{{.9}^4} + {9^3}.45} \right):\left( {{9^2}.10 – {9^2}} \right)\).

c) \(1024:{2^5} + 140:\left( {38 + {2^5}} \right) – {7^{23}}:{7^{21}}\).

d) \(12 – \left\{ {800:\left[ {537 – \left( {{2^5} + 15.7} \right)} \right]} \right\}{.1^{2021}}\).

e) \(1212:\left[ {\left( {{5^7}:{5^5}.6} \right) – {{\left( {20 – 13} \right)}^2}} \right]\).

f) \(25.\left\{ {{2^7}:\left[ {12 – 4 + {2^2}.\left( {16:{2^3}} \right)} \right] + {2^4}} \right\}\).

Bài 2. Tính hợp lí:

a) \({5^3}.73 – {5^3}.56 – 37.25\)

b) \(\left( {{{20.2}^4} + {{12.2}^4} – {{48.2}^2}} \right):{8^2}\)

c) \(42\left( {16 – 35} \right) – 35\left( {16 – 42} \right)\)

d) \(1152 – \left( {374 + 1152} \right) + \left( { – 65 + 374} \right)\)

e) \(\left( { – 1} \right) + \left( { – 3} \right) + … + \left( { – 199} \right) + \left( { – 201} \right)\)

f) \(17 + \left( { – 20} \right) + 23 + \left( { – 26} \right) + … + 53 + \left( { – 56} \right)\)

Bài 3. Tìm x biết:

a) \(\left[ {230 – \left( {15 – 5x} \right)} \right].3 = 390\)

b) \(345 – {5^{x – 3}} = {14^2} + 24\)

c) \(\left( {3x – {2^4}} \right){.7^3} = {2.7^4}\)

d) \(\left( {18 – 2x} \right)\left( {x – 8} \right) = 0\)

e) \(\left( {x + 2} \right)\left( {{x^2} + 4} \right) = 0\)

f) \({3^{x – 3}} – {3^2} = {2.3^2}\)

Bài 4. Tìm số nguyên x, y biết:

a) \(\overline {2x58y} \) chia hết cho cả 2; 5 và 9.

b) \(\overline {3x7y} \) chia hết cho 15.

c) \(60 \vdots x;140 \vdots x\) và \(5 \le x \le 20\).

d) \(x \vdots 12;x \vdots 15;x \vdots 18\) và \(x < 900\).

e) \(9 \vdots \left( {x + 2} \right)\)

f) \(\left( {x + 7} \right) \vdots \left( {x + 3} \right)\)

Bài 5. Cô giáo có 145 cái bút chì, 172 cái nhãn vở và 209 cái kẹo. Biết rằng khi cô chia đều số bút chì, số nhãn vở và kẹo cho các học sinh trong lớp thì cô còn thừa 9 cái bút chì, 2 cái nhãn vở và 5 cái kẹo. Hỏi lớp đó có bao nhiêu học sinh, biết số học sinh trong lớp lớn hơn 20 bạn. Khi đó mỗi bạn nhận được bao nhiêu bút chì, nhãn vở và kẹo?

Bài 6. Trong đợt quyên góp ủng hộ vở cho học sinh vùng cao, Liên đội thu được số vở từ 400 đến 500 quyển. Thầy tổng phụ trách cho xếp thành từng phần quà có 5 quyển, 6 quyển và 8 quyển thì đều thừa một quyển. Hỏi Liên đội thu được chính xác bao nhiêu quyển vở.

Bài 7. Cho hình vuông ABCD có AB = 30cm, hình vuông EFGH có EF = 24cm, biết AIGJ là một hình vuông và ABFE là một hình thang cân (hình vẽ bên).

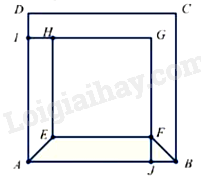
Tính diện tích hình vuông AIGJ và diện tích hình thang cân ABFE.

Bài 8. Nam dự định làm một mô hình cột cờ với các kích thước như hình vẽ bằng giấy bìa cứng. Tính diện tích giấy bìa tối thiểu cần sử dụng, biết là cờ tổ quốc là hình chữ nhật có kích thước 3cm x 2cm.

Bài 9. Ghép 6 hình tam giác đều thành một hình lục giác đều. Biết tổng chu vi của 6 hình tam giác đều là 90cm. Tính chu vi của hình lục giác đều được tạo thành.

Bài 10. Một mảnh vườn hình thoi có độ dài hai đường chéo là 9m và 6m. Giữa vườn người ta xây một bể cá hình vuông có độ dài mỗi cạnh là 2m và phần còn lại để trồng hoa, Tính diện tích phần vườn trồng hoa.

Bài 11*. Cho \(A = 4 + {4^2} + {4^3} + … + {4^{23}} + {4^{24}}\). Chứng minh: \(A \vdots 20;A \vdots 21;A \vdots 420\).

Bài 12*. Tìm số nguyên n để:

a) \(\left( {n – 14} \right) \vdots \left( {n + 2} \right)\)

b) \(\left( {4n + 7} \right) \vdots \left( {2n – 1} \right)\)

c) \(\left( {2n – 7} \right) \vdots \left( {3n + 5} \right)\)

——– Hết ——–

Lời giải chi tiết

I. Trắc nghiệm

II. Phần tự luận

Bài 1. Thực hiện phép tính:

a) \(425 + 378 – 125 + 122\).

b) \(\left( {{2^3}{{.9}^4} + {9^3}.45} \right):\left( {{9^2}.10 – {9^2}} \right)\).

c) \(1024:{2^5} + 140:\left( {38 + {2^5}} \right) – {7^{23}}:{7^{21}}\).

d) \(12 – \left\{ {800:\left[ {537 – \left( {{2^5} + 15.7} \right)} \right]} \right\}{.1^{2021}}\).

e) \(1212:\left[ {\left( {{5^7}:{5^5}.6} \right) – {{\left( {20 – 13} \right)}^2}} \right]\).

f) \(25.\left\{ {{2^7}:\left[ {12 – 4 + {2^2}.\left( {16:{2^3}} \right)} \right] + {2^4}} \right\}\).

Phương pháp

Áp dụng các phép tính với số tự nguyên, lũy thừa, quy tắc dấu ngoặc, thứ tự thực hiện phép tính.

Lời giải

a) \(425 + 378 – 125 + 122\)

\(\begin{array}{l} = \left( {425 – 125} \right) + \left( {378 + 122} \right)\\ = 300 + 500\\ = 800\end{array}\)

b) \(\left( {{2^3}{{.9}^4} + {9^3}.45} \right):\left( {{9^2}.10 – {9^2}} \right)\)

\(\begin{array}{l} = \left( {{{8.9}^4} + {9^3}.9.5} \right):\left[ {{9^2}\left( {10 – 1} \right)} \right]\\ = \left[ {{9^4}\left( {8 + 5} \right)} \right]:\left( {{9^2}.9} \right)\\ = \left( {{9^4}.13} \right):{9^3}\\ = 9.13\\ = 117\end{array}\)

c) \(1024:{2^5} + 140:\left( {38 + {2^5}} \right) – {7^{23}}:{7^{21}}\)

\(\begin{array}{l} = {2^{10}}:{2^5} + 140:\left( {38 + 32} \right) – {7^2}\\ = {2^5} + 140:70 – 49\\ = 32 + 2 – 49\\ = 34 – 49\\ =  – 15\end{array}\)

d) \(12 – \left\{ {800:\left[ {537 – \left( {{2^5} + 15.7} \right)} \right]} \right\}{.1^{2021}}\)

\(\begin{array}{l} = 12 – \left\{ {800:\left[ {537 – \left( {32 + 105} \right)} \right]} \right\}\\ = 12 – \left[ {800:\left( {537 – 137} \right)} \right]\\ = 12 – \left( {800:400} \right)\\ = 12 – 2\\ = 10\end{array}\)

e) \(1212:\left[ {\left( {{5^7}:{5^5}.6} \right) – {{\left( {20 – 13} \right)}^2}} \right]\)

\(\begin{array}{l} = 1212:\left[ {\left( {{5^2}.6} \right) – {7^2}} \right]\\ = 1212:\left( {150 – 49} \right)\\ = 1212:101\\ = 12\end{array}\)

f) \(25.\left\{ {{2^7}:\left[ {12 – 4 + {2^2}.\left( {16:{2^3}} \right)} \right] + {2^4}} \right\}\)

\(\begin{array}{l} = 25.\left\{ {{2^7}:\left[ {12 – 4 + {2^2}.\left( {{2^4}:{2^3}} \right)} \right] + {2^4}} \right\}\\ = 25.\left\{ {{2^7}:\left[ {8 + {2^2}.2} \right] + {2^4}} \right\}\\ = 25.\left\{ {{2^7}:\left[ {8 + 8} \right] + {2^4}} \right\}\\ = 25.\left( {{2^7}:{2^4} + {2^4}} \right)\\ = 25\left( {{2^3} + {2^4}} \right)\\ = 25\left( {8 + 16} \right)\\ = 25.24\\ = 600\end{array}\)

Bài 2. Tính hợp lí:

a) \({5^3}.73 – {5^3}.56 – 37.25\)

b) \(\left( {{{20.2}^4} + {{12.2}^4} – {{48.2}^2}} \right):{8^2}\)

c) \(42\left( {16 – 35} \right) – 35\left( {16 – 42} \right)\)

d) \(1152 – \left( {374 + 1152} \right) + \left( { – 65 + 374} \right)\)

e) \(\left( {{{20.2}^4} + {{12.2}^4} – {{48.2}^2}} \right):{8^2}\)

f) \(\left( { – 1} \right) + \left( { – 3} \right) + … + \left( { – 199} \right) + \left( { – 201} \right)\)

g) \(17 + \left( { – 20} \right) + 23 + \left( { – 26} \right) + … + 53 + \left( { – 56} \right)\)

Phương pháp

Áp dụng các phép tính với số tự nguyên, lũy thừa, quy tắc dấu ngoặc, thứ tự thực hiện phép tính.

f, g: Sử dụng công thức tính tổng n số hạng: \({S_n} = {{\left( {{a_1} + {a_n}} \right).n}}:{2}\) (n là số số hạng)

Lời giải

a) \({5^3}.73 – {5^3}.56 – 37.25\)

\(\begin{array}{l} = {5^3}\left( {73 – 56} \right) – 37.25\\ = {5^3}.17 – 37.25\\ = 25.5.17 – 37.25\\ = 25\left( {5.17 – 37} \right)\\ = 25.48\\ = 1200\end{array}\)

b) \(\left( {{{20.2}^4} + {{12.2}^4} – {{48.2}^2}} \right):{8^2}\)

\(\begin{array}{l} = \left( {{{20.2}^4} + {{12.2}^4} – {{12.2}^2}{{.2}^2}} \right):{\left( {{2^3}} \right)^2}\\ = \left( {{{20.2}^4} + {{12.2}^4} – {{12.2}^4}} \right):{2^6}\\ = \left[ {\left( {20 + 12 – 12} \right){{.2}^4}} \right]:{2^6}\\ = \left( {{{20.2}^4}} \right):{2^6}\\ = \left( {{{5.2}^2}{{.2}^4}} \right):{2^6}\\ = \left( {{{5.2}^6}} \right):{2^6}\\ = 5\end{array}\)

c) \(42\left( {16 – 35} \right) – 35\left( {16 – 42} \right)\)

\(\begin{array}{l} = 42.16 – 42.35 – 35.16 + 35.42\\ = \left( {42.16 – 35.16} \right) + \left( { – 42.35 + 35.42} \right)\\ = 16\left( {42 – 35} \right)\\ = 16.7\\ = 112\end{array}\)

d) \(1152 – \left( {374 + 1152} \right) + \left( { – 65 + 374} \right)\)

\(\begin{array}{l} = 1152 – 374 – 1152 – 65 + 374\\ = \left( {1152 – 1152} \right) – \left( {374 – 374} \right) – 65\\ =  – 65\end{array}\)

e) \(\left( { – 1} \right) + \left( { – 3} \right) + … + \left( { – 199} \right) + \left( { – 201} \right)\)

\( =  – \left( {1 + 3 + … + 199 + 201} \right)\) (có 101 số số hạng)

\(\begin{array}{l} =  – {{\left( {1 + 201} \right).101}}:{2}\\ =  – 10201\end{array}\)

f) \(17 + \left( { – 20} \right) + 23 + \left( { – 26} \right) + … + 53 + \left( { – 56} \right)\)

\(\begin{array}{l} = \left( {17 + 23 + … + 53} \right) – (20 + 26 + … + 56)\\ = {{\left( {17 + 53} \right).7}}:{2} – {{\left( {20 + 56} \right).7}}:{2}\\ = 245 – 266\\ =  – 21\end{array}\)

Bài 3. Tìm x biết:

a) \(\left[ {230 – \left( {15 – 5x} \right)} \right].3 = 390\)

b) \(345 – {5^{x – 3}} = {14^2} + 24\)

c) \(\left( {3x – {2^4}} \right){.7^3} = {2.7^4}\)

d) \(\left( {18 – 2x} \right)\left( {x – 8} \right) = 0\)

e) \(\left( {x + 2} \right)\left( {{x^2} + 4} \right) = 0\)

f) \({3^{x – 3}} – {3^2} = {2.3^2}\)

Phương pháp

– Thực hiện các phép toán với số tự nhiên.

– Vận dụng kiến thức lũy thừa với số mũ tự nhiên

Hai lũy thừa cùng cơ số bằng nhau khi số mũ của chúng bằng nhau.

\(A.B = 0 \Rightarrow A = 0\) hoặc \(B = 0\).

Lời giải

a) \(\left[ {230 – \left( {15 – 5x} \right)} \right].3 = 390\)

\(\begin{array}{l}230 – \left( {15 – 5x} \right) = 390:3\\230 – \left( {15 – 5x} \right) = 130\\15 – 5x = 230 – 130\\15 – 5x = 100\\5x = 15 – 100\\5x =  – 85\\x =  – 17\end{array}\)

Vậy x = -17.

b) \(345 – {5^{x – 3}} = {14^2} + 24\)

\(\begin{array}{l}345 – {5^{x – 3}} = 196 + 24\\345 – {5^{x – 3}} = 220\\{5^{x – 3}} = 125\\{5^{x – 3}} = {5^3}\\x – 3 = 3\\x = 6\end{array}\)

Vậy x = 6.

c) \(\left( {3x – {2^4}} \right){.7^3} = {2.7^4}\)

\(\begin{array}{l}3x – {2^4} = {2.7^4}:{7^3}\\3x – {2^4} = 2.7\\3x – 16 = 14\\3x = 14 + 16\\3x = 30\\x = 10\end{array}\)

Vậy x =10.

d) \(\left( {18 – 2x} \right)\left( {x – 8} \right) = 0\)

\(18 – 2x = 0\) hoặc \(x – 8 = 0\)

\(\begin{array}{l}2x = 18\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 8\,\\x = 9\end{array}\)

Vậy \(x \in \left\{ {8;9} \right\}\).

e) \(\left( {x + 2} \right)\left( {{x^2} + 4} \right) = 0\)

\(x + 2 = 0\) hoặc \({x^2} + 4 = 0\)

\(x =  – 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x^2} =  – 4\) (không thỏa mãn vì \({x^2} \ge 0\,\forall x \in \mathbb{Z}\))

Vậy x = -2.

f) \({3^{x – 3}} – {3^2} = {2.3^2}\)

\(\begin{array}{l}{3^{x – 3}} = {2.3^2} + {3^2}\\{3^{x – 3}} = {3.3^2}\\{3^{x – 3}} = {3^3}\\x – 3 = 3\\x = 6\end{array}\)

Vậy x = 6.

Bài 4. Tìm số nguyên x, y biết:

a) \(\overline {2x58y} \) chia hết cho cả 2; 5 và 9

b) \(\overline {3x7y} \) chia hết cho 15

c) \(60 \vdots x;140 \vdots x\) và \(5 \le x \le 20\)

d) \(x \vdots 12;x \vdots 15;x \vdots 18\) và \(x < 900\)

e) \(9 \vdots \left( {x + 2} \right)\)

f) \(\left( {x + 7} \right) \vdots \left( {x + 3} \right)\)

Phương pháp

Sử dụng kiến thức về dấu hiệu chia hết, ước chung, bội chung.

Lời giải

a) \(\overline {2x58y} \) chia hết cho cả 2; 5 và 9

Để \(\overline {2x58y} \) chia hết cho 2 và 5 thì y = 0, ta được số \(\overline {2×580} \).

Để \(\overline {2×580} \) chia hết cho 9 thì \(\left( {2 + x + 5 + 8 + 0} \right) \vdots 9\) \( \Rightarrow \left( {15 + x} \right) \vdots 9 \Rightarrow x = 3\), ta được số \(23580\).

Vậy x = 3, y = 0.

b) \(\overline {3x7y} \) chia hết cho 15

Ta có: 15 = 3.5

Để \(\overline {3x7y} \) chia hết cho 15 thì \(\overline {3x7y} \) chia hết cho 3 và 5.

Để \(\overline {3x7y} \) chia hết cho 5 thì y = 0 hoặc y = 5.

Với y = 0, ta được số \(\overline {3×70} \). Để \(\overline {3×70} \) chia hết cho 3 thì \(\left( {3 + x + 7 + 0} \right) \vdots 3 \Rightarrow \left( {10 + x} \right) \vdots 3 \Rightarrow x \in \left\{ {2;5;8} \right\}\).

Với y = 5, ta được số \(\overline {3×75} \). Để \(\overline {3×75} \) chia hết cho 3 thì \(\left( {3 + x + 7 + 5} \right) \vdots 3 \Rightarrow \left( {15 + x} \right) \vdots 3 \Rightarrow x \in \left\{ {0;3;6;9} \right\}\).

Vậy với y = 0 thì \(x \in \left\{ {2;5;8} \right\}\); với y = 5 thì \(x \in \left\{ {0;3;6;9} \right\}\).

c) \(60 \vdots x;140 \vdots x\) và \(5 \le x \le 20\)

Vì \(60 \vdots x;140 \vdots x \Rightarrow x \in \)ƯC\(\left( {60;140} \right)\)

Ta có: \(\left\{ \begin{array}{l}60 = {2^2}.3.5\\140 = {2^2}.5.7\end{array} \right. \Rightarrow \)ƯCLN\(\left( {60;140} \right) = {2^2}.5 = 20\)

\( \Rightarrow \)ƯC\(\left( {60;140} \right)\)= Ư\(\left( {20} \right) = \left\{ { \pm 1; \pm 2; \pm 4; \pm 5; \pm 10; \pm 20} \right\}\)

Mà \(5 \le x \le 20 \Rightarrow x \in \left\{ {5;10;20} \right\}\)

Vậy \(x \in \left\{ {5;10;20} \right\}\).

d) \(x \vdots 12;x \vdots 15;x \vdots 18\) và \(x < 900\)

Vì \(x \vdots 12;x \vdots 15;x \vdots 18\) nên \(x \in BC\left( {12;15;18} \right)\)

Ta có: \(\left\{ \begin{array}{l}12 = {2^2}.3\\15 = 3.5\\18 = {2.3^2}\end{array} \right. \Rightarrow BCNN\left( {12;15;18} \right) = {2^2}{.3^2}.5 = 180\)

\( \Rightarrow BC\left( {12;15;18} \right) = B\left( {180} \right) = \left\{ {0;180;360;540;720;900;…} \right\}\)

Mà \(x < 900 \Rightarrow x \in \left\{ {0;180;360;540;720} \right\}\)

Vậy \(x \in \left\{ {0;180;360;540;720} \right\}\)

e) \(9 \vdots \left( {x + 2} \right)\)

Vì \(9 \vdots \left( {x + 2} \right)\) nên \(\left( {x + 2} \right) \in \)Ư\(\left( 9 \right)\).

Ư\(\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\)

Ta có bảng giá trị sau:

Vậy \(x \in \left\{ { – 11; – 5; – 3; – 1;1;7} \right\}\)

f) \(\left( {x + 7} \right) \vdots \left( {x + 3} \right)\)

Ta có:

\(\begin{array}{l}\left( {x + 7} \right) \vdots \left( {x + 3} \right)\\ \Rightarrow \left( {x + 3 + 4} \right) \vdots \left( {x + 3} \right)\end{array}\)

Vì \(\left( {x + 3} \right) \vdots \left( {x + 3} \right) \Rightarrow 4 \vdots \left( {x + 3} \right) \Rightarrow \left( {x + 3} \right) \in \)Ư\(\left( 4 \right)\)

Ư\(\left( 4 \right) = \left\{ { \pm 1; \pm 2; \pm 4} \right\}\)

Ta có bảng giá trị sau:

Vậy \(x \in \left\{ { – 7; – 5; – 4; – 2; – 1;1} \right\}\)

Bài 5. Cô giáo có 145 cái bút chì, 172 cái nhãn vở và 209 cái kẹo. Biết rằng khi cô chia đều số bút chì, số nhãn vở và kẹo cho các học sinh trong lớp thì cô còn thừa 9 cái bút chì, 2 cái nhãn vở và 5 cái kẹo. Hỏi lớp đó có bao nhiêu học sinh, biết số học sinh trong lớp lớn hơn 20 bạn. Khi đó mỗi bạn nhận được bao nhiêu bút chì, nhãn vở và kẹo?

Phương pháp

Gọi số học sinh là x. Sử dụng kiến thức về ước chung để tìm x.

Thực hiện phép chia để tính số bút chì, nhãn vở và kẹo mỗi bạn nhận được.

Lời giải

Gọi số học sinh là x (học sinh), \(x \in \mathbb{N}*;x > 20\).

Vì khi cô chia đều số bút chì, số nhãn vở và kẹo cho các học sinh trong lớp thì cô còn thừa 9 cái bút chì, 2 cái nhãn vở và 5 cái kẹo nên:

Số bút chì chia hết là: 145 – 9 = 136 (cái)

Số nhãn vở chia hết là: 172 – 2 = 170 (cái)

Số kẹo chia hết là: 209 – 5 = 204 (cái)

\( \Rightarrow 136 \vdots x;170 \vdots x;204 \vdots x\) hay \(x \in \)ƯC\(\left( {136;170;204} \right)\).

Ta có: \(\left\{ \begin{array}{l}136 = {2^3}.17\\170 = 2.5.17\\204 = {2^2}.3.17\end{array} \right. \Rightarrow \)ƯCLN\(\left( {136;170;204} \right) = 2.17 = 34\)

\( \Rightarrow \)ƯC \(\left( {136;170;204} \right) = \)Ư\(\left( {34} \right) = \left\{ { \pm 1; \pm 2; \pm 17; \pm 34} \right\}\)\( \Rightarrow x \in \left\{ { \pm 1; \pm 2; \pm 17; \pm 34} \right\}\)

Mà x > 20 \( \Rightarrow x = 34\).

\( \Rightarrow \) Mỗi bạn nhận được số bút chì là: 136 : 34 = 4 (cái)

Mỗi bạn nhận được số nhãn vở là: 170 : 34 = 5 (cái)

Mỗi bạn nhận được số kẹo là: 204 : 34 = 6 (cái)

Vậy mỗi bạn nhận được 4 cái bút chì, 5 cái nhãn vở và 6 cái kẹo.

Bài 6. Trong đợt quyên góp ủng hộ vở cho học sinh vùng cao, Liên đội thu được số vở từ 400 đến 500 quyển. Thầy tổng phụ trách cho xếp thành từng phần quà có 5 quyển, 6 quyển và 8 quyển thì đều thừa một quyển. Hỏi Liên đội thu được chính xác bao nhiêu quyển vở.

Phương pháp

Gọi số quyển vở là x. Sử dụng kiến thức về bội chung để tìm x.

Lời giải

Gọi số quyển vở Liên đội thu được là x (quyển), \(x \in \mathbb{N}*;400 \le x \le 500\).

Vì khi xếp thành từng phần quà có 5 quyển, 6 quyển và 8 quyển thì đều thừa một quyển nên x – 1 chia hết cho 5, 6 và 8 \( \Rightarrow \left( {x – 1} \right) \in BC\left( {5,6,8} \right)\).

Ta có: \(\left\{ \begin{array}{l}5 = 1.5\\6 = 2.3\\8 = {2^3}\end{array} \right. \Rightarrow BCNN\left( {5;6;8} \right) = {2^3}.3.5 = 120\)

\( \Rightarrow BC\left( {5;6;8} \right) = B\left( {120} \right) = \left\{ {0;120;240;360;480;600;…} \right\}\)

\(\begin{array}{l} \Rightarrow x – 1 \in \left\{ {0;120;240;360;480;600;…} \right\}\\ \Rightarrow x \in \left\{ {1;121;241;361;481;601;…} \right\}\end{array}\)

Mà \(400 \le x \le 500 \Rightarrow x = 481\)

Vậy Liên đội thu được 481 quyển vở.

Bài 7. Cho hình vuông ABCD có AB = 30cm, hình vuông EFGH có EF = 24cm, biết AIGJ là một hình vuông và ABFE là một hình thang cân (hình vẽ bên).

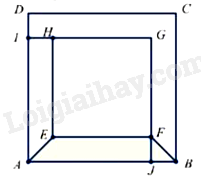
Tính diện tích hình vuông AIGJ và diện tích hình thang cân ABFE.

Phương pháp

Kẻ HE cắt AB tại K.

Chia hình thang cân AEFB thành hai tam giác vuông AEK, BFJ và hình chữ nhật EFJK.

Tính độ dài BJ, AK dựa vào AB.

Tính EK, FJ theo BJ, AK.

Sử dụng công thức tính diện tích hình vuông và diện tích hình thang cân.

Lời giải

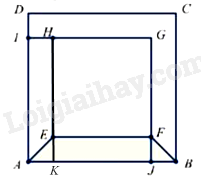
Kẻ HE cắt AB tại K, gọi BJ = x (x > 0).

\(\begin{array}{l} \Rightarrow BJ = AK = x,EF = KJ\\ \Rightarrow BJ + AK + KJ = AB\\x + x + KJ = AB\\2x + 24 = 30\\2x = 6\\x = 3\left( {cm} \right)\end{array}\)

Vì AIGJ là hình vuông nên IG = GJ = AJ = AI.

HGEF là hình vuông nên HG = GF = EF = HE

\( \Rightarrow \) IG – HG = GJ – GF = AJ – EF

\( \Rightarrow \) HI = FJ = AK = 3 cm

\( \Rightarrow {S_{ABEF}} = \left( {{\rm{EF + AB}}} \right).FJ:2 = \left( {24 + 30} \right).3:2 = 81\left( {c{m^2}} \right)\)

Ta có: IG = IH + HG = 3 + 24 = 27 (cm)

\( \Rightarrow {S_{AIGJ}} = {27^2} = 729\left( {c{m^2}} \right)\)

Vậy diện tích hình vuông AIGJ là 729 cm², diện tích hình thang cân AEFB là 81 cm².

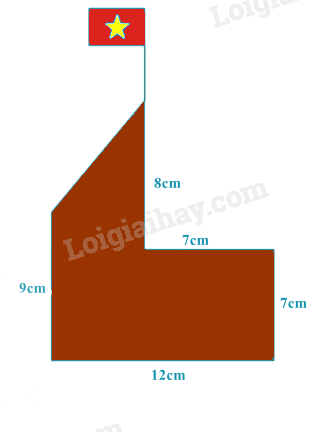
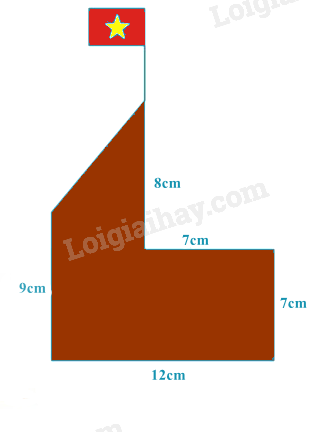
Bài 8. Nam dự định làm một mô hình cột cờ với các kích thước như hình vẽ bằng giấy bìa cứng. Tính diện tích giấy bìa tối thiểu cần sử dụng, biết là cờ tổ quốc là hình chữ nhật có kích thước 3cm x 2cm.

Phương pháp

Sử dụng công thức tính diện tích hình thang, hình chữ nhật.

Lời giải

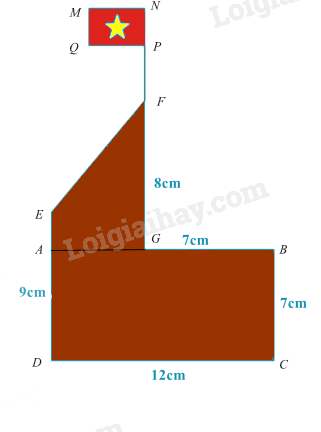
Gọi các điểm như hình vẽ. Ta có mô hình cột cờ được chia thành một hình chữ nhật ABCD và hình thang vuông AEFG.

Ta có ABCD là hình chữ nhật nên AD = BC \( \Rightarrow \) AE = DE – AD = DE – BC = 8 – 7 = 1 (cm)

AB = CD nên AG = AB – GB = CD – GB = 12 – 7 = 5 (cm)

Diện tích hình chữ nhật ABCD là: \({S_{ABCD}} = 12.7 = 84\left( {c{m^2}} \right)\)

Diện tích hình thang vuông AEFG là: \({S_{AEFG}} = \left( {AE + FG} \right).AG:2 = \left( {1 + 9} \right).5:2 = 25\left( {c{m^2}} \right)\)

Diện tích lá cờ MNPQ là: \({S_{MNPQ}} = 2.3 = 6\left( {c{m^2}} \right)\)

Diện tích giấy bìa tối thiểu cần sử dụng là: \(84 + 25 + 6 = 115\left( {c{m^2}} \right)\)

Vậy diện tích giấy bìa tối thiểu cần sử dụng là 115 cm².

Bài 9. Ghép 6 hình tam giác đều thành một hình lục giác đều. Biết tổng chu vi của 6 hình tam giác đều là 90cm. Tính chu vi của hình lục giác đều được tạo thành.

Phương pháp

Dựa vào công thức tính chu vi hình tam giác đều đều tính độ dài cạnh. Tính số cạnh của hình lục giác để tính được chu vi hình lục giác.

Lời giải

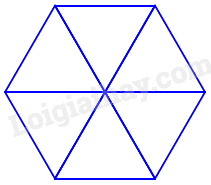
Vì tổng chu vi 6 hình tam giác đều là 90cm nên chu vi một hình tam giác đều là:

90 : 6 = 15 (cm)

Vì chu vi một hình tam giác đều là 15cm nên cạnh của hình tam giác đều đó là:

15 : 3 = 5 (cm)

Vì hình lục giác đều có 6 cạnh nên chu vi hình lục giác đều đó là:

5 . 6 = 30 (cm)

Vậy chu vi hình lục giác đều được tạo thành là 30 cm.

Bài 10. Một mảnh vườn hình thoi có độ dài hai đường chéo là 9m và 6m. Giữa vườn người ta xây một bể cá hình vuông có độ dài mỗi cạnh là 2m và phần còn lại để trồng hoa, Tính diện tích phần vườn trồng hoa.

Phương pháp

Sử dụng công thức tính diện tích hình vuông, diện tích hình thoi.

Diện tích phần vườn trồng hoa bằng diện tích mảnh vườn trừ diện tích bể cá.

Lời giải

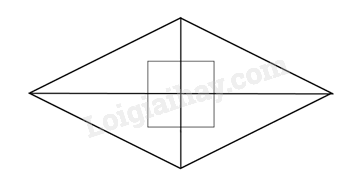
Diện tích mảnh vườn là: \(9.6:2 = 27\left( {{m^2}} \right)\)

Diện tích bể cá là: \(2.2 = 4\left( {{m^2}} \right)\)

Diện tích phần vườn trồng hoa là: \(27 – 4 = 23\left( {{m^2}} \right)\)

Vậy diện tích phần vườn trồng hoa là 23 m².

Bài 11*. Cho \(A = 4 + {4^2} + {4^3} + … + {4^{23}} + {4^{24}}\). Chứng minh: \(A \vdots 20;A \vdots 21;A \vdots 420\).

Phương pháp

Nhóm các số hạng trong A thành các tổng để chứng minh.

Lời giải

Ta có: 420 = 21.20 nên ta chỉ cần chứng minh \(A \vdots 20;A \vdots 21\).

+) Ta có:

\(\begin{array}{l}A = 4 + {4^2} + {4^3} + … + {4^{23}} + {4^{24}}\\ = \left( {4 + {4^2}} \right) + \left( {{4^3} + {4^4}} \right) + … + \left( {{4^{23}} + {4^{24}}} \right)\\ = \left( {4 + {4^2}} \right) + {4^2}\left( {4 + {4^2}} \right) + … + {4^{22}}\left( {4 + {4^2}} \right)\\ = 20 + {20.4^2} + … + {20.4^{22}}\\ = 20.\left( {1 + {4^2} + … + {4^{22}}} \right)\end{array}\)

Vì \(20 \vdots 20 \Rightarrow \left( {20.\left( {1 + {4^2} + … + {4^{22}}} \right)} \right) \vdots 20 \Rightarrow A \vdots 20\)

+) Ta có:

\(\begin{array}{l}A = 4 + {4^2} + {4^3} + … + {4^{23}} + {4^{24}}\\ = \left( {4 + {4^2} + {4^3}} \right) + \left( {{4^4} + {4^5} + {4^6}} \right) + … + \left( {{4^{22}} + {4^{23}} + {4^{24}}} \right)\\ = \left( {4 + {4^2} + {4^3}} \right) + {4^3}\left( {4 + {4^2} + {4^3}} \right) + … + {4^{21}}\left( {4 + {4^2} + {4^3}} \right)\\ = \left( {4 + {4^2} + {4^3}} \right)\left( {1 + {4^3} + … + {4^{21}}} \right)\\ = 84.\left( {1 + {4^3} + … + {4^{21}}} \right)\end{array}\)

Vì \(84 \vdots 21 \Rightarrow \left( {84.\left( {1 + {4^3} + … + {4^{21}}} \right)} \right) \vdots 21 \Rightarrow A \vdots 21\)

Vì \(A \vdots 20;A \vdots 21\) nên \(A \vdots 420\)

Vậy \(A \vdots 20;A \vdots 21;A \vdots 420\)

Bài 12*. Tìm số nguyên n để:

a) \(\left( {n – 14} \right) \vdots \left( {n + 2} \right)\)

b) \(\left( {4n + 7} \right) \vdots \left( {2n – 1} \right)\)

c) \(\left( {2n – 7} \right) \vdots \left( {3n + 5} \right)\)

Phương pháp

Sử dụng kiến thức về ước để tìm n.

Lời giải

a) Ta có:

\(\begin{array}{l}\left( {n – 14} \right) \vdots \left( {n + 2} \right)\\\left( {n + 2 – 16} \right) \vdots \left( {n + 2} \right)\end{array}\)

Vì \(\left( {n + 2} \right) \vdots \left( {n + 2} \right) \Rightarrow  – 16 \vdots \left( {n + 2} \right) \Rightarrow \left( {n + 2} \right) \in \)Ư\(\left( { – 16} \right)\)

Ư\(\left( { – 16} \right) = \left\{ { \pm 1; \pm 2; \pm 4; \pm 8; \pm 16} \right\}\)

Ta có bảng giá trị sau:

Vậy \(n \in \left\{ { – 18; – 10; – 6; – 4; – 3; – 1;0;2;6;14} \right\}\).

b) Ta có:

\(\begin{array}{l}\left( {4n + 7} \right) \vdots \left( {2n – 1} \right)\\\left( {4n – 2 + 9} \right) \vdots \left( {2n – 1} \right)\end{array}\)

Vì \(\left( {4n – 2} \right) \vdots \left( {2n – 1} \right) \Rightarrow 9 \vdots \left( {2n – 1} \right) \Rightarrow \left( {2n – 1} \right) \in \)Ư\(\left( 9 \right)\)

Ư\(\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\)

Ta có bảng giá trị sau:

Vậy \(n \in \left\{ { – 4; – 1;0;1;2;5} \right\}\).

c) Ta có:

\(\begin{array}{l}\left( {2n – 7} \right) \vdots \left( {3n + 5} \right)\\ \Rightarrow 3\left( {2n – 7} \right) \vdots \left( {3n + 5} \right)\\\left( {6n – 21} \right) \vdots \left( {3n + 5} \right)\\\left( {6n + 10 – 31} \right) \vdots \left( {3n + 5} \right)\end{array}\)

Vì \(\left( {6n + 10} \right) \vdots \left( {3n + 5} \right) \Rightarrow  – 31 \vdots \left( {3n + 5} \right) \Rightarrow \left( {3n + 5} \right) \in \)Ư\(\left( { – 31} \right)\)

Ư\(\left( { – 31} \right) = \left\{ { \pm 1; \pm 31} \right\}\)

Ta có bảng giá trị sau:

Vậy \(n \in \left\{ { – 12; – 2} \right\}\).